The Four Curves of Alexis Clairaut
Alexis Clairaut, born in 1713 to mathematician and teacher Jean-Baptiste Clairaut and mother Catherine, was a mathematician who showed promise from a very young age. In 1726 he presented on four new families of curves and their properties to the French Royal Academy of Sciences. Clairaut published these findings in 1734 in “Quatre Problèmes sur de Nouvelles Courbes” (“Four Problems on New Curves”) in the fourth volume of the journal of the Royal Prussian Academy of Sciences, Miscellanea berolinensia ad incremental scientiarum. Each of the four families of algebraic curves that he investigated was partly motivated by the classical Greek problem of finding mean proportionals between two given line segments. Clairaut also investigated the analytic properties of his curves by finding tangents, inflection points, and quadratures.
Clairaut’s 1734 paper, written and published in French, has not yet been translated to English. We present a dual language edition—French (pdf) and English (pdf)—to make Clairaut’s paper accessible by a modern audience.
In this companion article, we provide an overview of the historical and mathematical contexts of Clairaut's paper, relating his work in particular to that of Descartes. We then describe the provenance of Clairaut's text and the editorial conventions that we adopted in preparing its French transcription and English translation. This is followed by some brief technical notes to help a modern reader better understand the problem of finding mean proportionals that played the central role in Clairaut's findings, as well as his use of the French mathematical term genre. We close with a few comments about what Clairaut's paper might offer today's students, based on our own experience as a faculty-student research-and-translation team.
The Four Curves of Alexis Clairaut: Introduction

Figure 1: Alexis Clairaut (1713–1765).
Convergence Portrait Gallery.
Alexis Clairaut was born 7 May 1713 in Paris, to father Jean-Baptiste and mother Catherine (née Petit). His father was a mathematician and teacher. Alexis began to learn at home from a young age and proved a veritable prodigy. He is said to have learned the alphabet from the diagrams in Euclid’s Elements (though, to be fair, this may have been intended tongue-in-cheek, as in, He was studying mathematics so early that he was reading Euclid at the same time he was learning the alphabet!). Certainly, at age four he could read and write well. By nine, he had studied Nicolas Guisnée’s 1705 Application de l’algèbre à la géométrie [9] under the guidance of his father. At ten, he began studying Traité analytique des sections coniques (1720) and Analyse des infiniment petits (1696), both by L’Hôpital. For further details about Clairaut’s life and work, see [4; 8; 10].
On 18 May 1726, just a few days after his thirteenth birthday, Clairaut presented his research on four families of algebraic curves to the Royal Academy of Sciences in Paris. This work was later published, in 1734, in volume 4 of the Miscellanea Berolinensia under the title “Quatre Problèmes sur de Nouvelles Courbes” [2]. It was preceded by a paper written by his father, which concerned inscribing solid figures inside other solid figures. The younger Clairaut is referred to in the publication as Mr. Alexis Clairaut, le Fils, although the contents of his paper clearly are more sophisticated than those in his father’s article. The end of the younger Clairaut’s article bears a note, signed by Bernard de Fontanelle, indicating that he was examined by François Nicole and Henri Pitot on this date (18 May) and recognizing that he was twelve and a half when developing this material.
Clairaut’s curves were partly motivated by the classical Greek problem of finding any number of mean proportionals between two given segments. The case of one mean proportional is given in Euclid's Elements (VI.13). Finding two mean proportionals is sufficient to solve the problem of duplicating a cube; a wealth of solutions were known in antiquity and were recorded by Eutocius of Ascalon. One solution, due to Eratosthenes, permits solving the more general problem of finding any number of mean proportionals. Some early modern mathematicians revisited these ancient solutions; in particular, the next section considers work by Descartes that explores one of the same families of curves that would later be taken up by Clairaut.
The Four Curves of Alexis Clairaut: Descartes’ Geometrie
As noted in the previous section, René Descartes (1596–1650) was one of several early modern mathematicians who revisited the ancient solutions to the problem of constructing mean proportionals. In his 1637 La Géométrie, Descartes criticized (in an indirect way) Greek mathematicians for the complicated nature of their solutions to this problem. At the beginning of Book III, he revisited his mesolabe compass, a pseudo-mechanical device which he described in Book II. This device, he believed, provides the easiest manner of finding any number of means:
For example, there is, I believe, no easier method of finding any number of mean proportionals, nor one whose demonstration is clearer, than the one which employs the curves described by the instrument \(XYZ\), previously explained. [3, p. 155]
Descartes’ mesolabe compass, which he called “instrument \(XYZ\)”, consists of a number of sliding straightedges linked together. One straightedge, \(YZ\), remains fixed and, in the diagram below, horizontal. Another straightedge, \(YX\), is attached to \(YZ\) with a hinge at \(Y\). A point \(A\) is chosen on the horizontal segment \(YZ\), with \(B\) chosen to be at the same distance from \(Y\) as \(A\) is. As the hinge is opened, the point \(B\) traces out an arc of a circle.
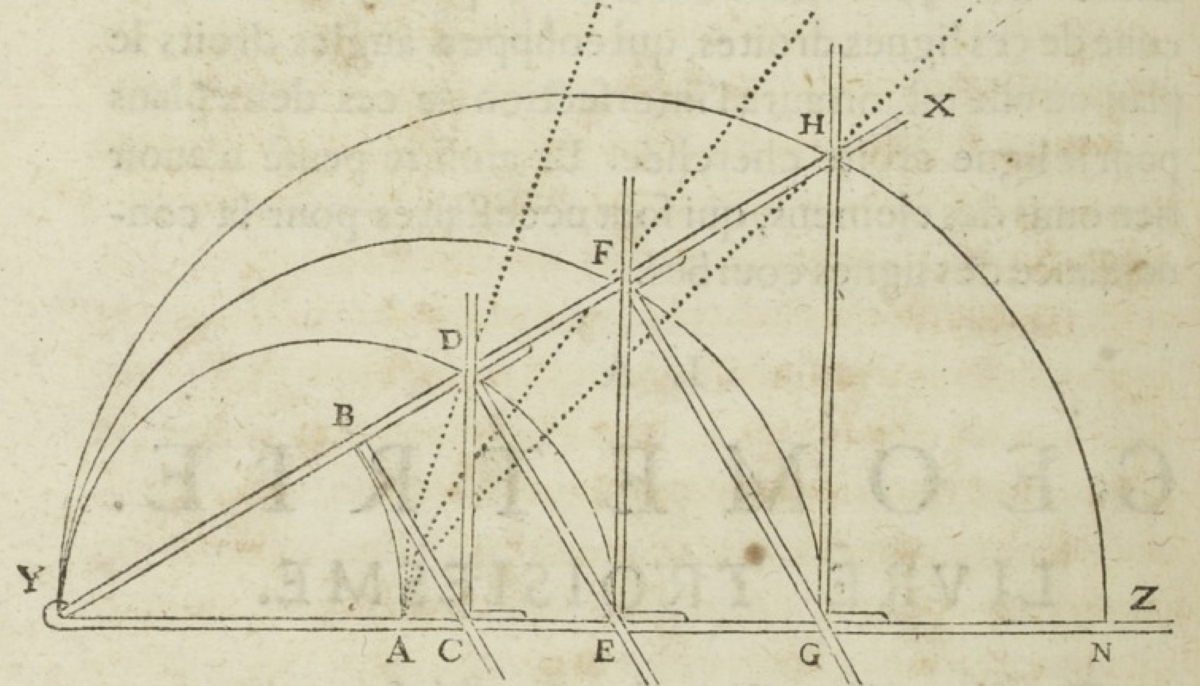
Figure 2: Descartes’ Mesolabe Compass, [3, pp. 46, 154]. gallica.bnf.fr / Bibliothèque nationale de France.
At \(B\), a perpendicular segment \(BC\) is drawn, and the point at which it intersects the horizontal \(YZ\) is marked as \(C\). A perpendicular to the horizontal is drawn from \(C\), intersecting the segment \(YX\) at \(D\). This process of dropping a perpendicular from \(YX\) and then drawing a perpendicular from \(YZ\) can be performed as many times as one wishes: Descartes’ diagram has three downward perpendiculars and three vertical perpendiculars.
As the hinge is opened, the point \(B\) induces a movement of the other intersection points. If we track the movement of \(D\), for example, a curve is traced out. Letting the radius \(YA = a\), we can find the equation for this curve:
\(x^4 = a^2(x^2 + y^2)\),
which is the same as Clairaut’s first curve (with one exception: Clairaut gave \(y^4 = a^2(x^2 + y^2)\), but this merely exchanges the \(x\) and \(y\) axes; see Editorial Conventions: General below for more on this issue). Descartes himself did not explicitly give the equations for the curves traced by \(D\), \(F\), or \(H\), but these are
\(x^8 = a^2(x^2 + y^2)^3\) and
\(x^{12} = a^2(x^2 + y^2)^5\),
respectively.[1] Again, these curves are covered by Clairaut’s first family, for appropriate choices of Clairaut’s index \(n\). For convenience Clairaut sometimes set \(a = 1\). For the diagrams, we generally have used \(a = 1\), but on occasion use \(a = 1.25\) or \(a = 1.5\) for the sake of spacing.
The Four Curves of Alexis Clairaut: Clairaut’s Work
The power of the mesolabe compass, then, is not that it solves the specific case of two mean proportionals. Rather, it is able to solve for any number of means. Similarly, Clairaut’s curves started from a desire to solve a specific problem, but he quickly generalized them to produce a family of curves able to solve the general problem of finding any number of means. Clairaut’s work differs from Descartes’ in a number of ways:
-
Clairaut’s first family of curves is a proper super-set of the curves described by Descartes’ mesolabe compass. Clairaut placed an intermediate curve between each of Descartes’.
-
Clairaut gave three other families of curves, similarly motivated, but totally different in construction.
- Clairaut also investigated properties of his curves such as their tangents and inflection points. This point especially should not be seen as a criticism of Descartes: after all, a considerable amount of time transpired between the first edition of La Géométrie and Clairaut’s paper.
The first point is illustrated in the following figure. The construction given by Descartes is shown, with his curves traced in red. The curves unique to Clairaut are shown in blue.
The equations for each of these curves is listed below, indexed under both Clairaut’s scheme and Descartes’. In the figure, the curves move from left to right from \(Y\) towards \(X\), alternating between red and blue.
Taking \(a = 1\), the general form for Clairaut’s equation is
\(x^{\frac{n + 1}{n}} = \sqrt{x^2 + y^2}\).
When \(n\) is even, raising both sides to the \(n\)th power clears the fractional exponents, yielding the polynomial equation
\(x^{n+1} = (x^2 + y^2)^{\frac{n}{2}}\) (for n even).
If, however, \(n\) is odd, then it is necessary to raise both sides to the \(2n\)th power, yielding
\(x^{2n+2} = (x^2 + y^2)^n\) (for \(n\) odd).
This yields the following list of equations, whose graphs are shown in Figure 3:
- C1/D1: \(x^4 = x^2 + y^2\)
- C2: \(x^3 = x^2 + y^2\)
- C3/D2: \(x^8 = (x^2 + y^2)^3\)
- C4: x5 = \((x^2 + y^2)^2\)
- C5/D3: \(x^{12} = (x^2 + y^2)^5\)
Figure 2: Descartes’ and Clairaut’s Curves.
The cases where we take \(n\) odd in Clairaut’s general equation yield precisely the curves given by Descartes.
Given the degree to which Clairaut’s work relates to Descartes’, it is surprising that Clairaut never mentioned Descartes or La Géométrie. In fact, Clairaut never mentioned any other mathematician or work, not even Guisnée, despite using almost precisely the same assignment of points and quantities as Guisnée. Guisnée himself referenced Descartes by name four times. We have a hard time believing that Clairaut had not read Descartes. Even if he had failed to notice the similarity of his curves with those of Descartes when he presented this work, we would expect that someone at the Royal Academy would have. We also would find it strange that, even if he had not noticed the similarity when he presented to the Academy, he would not have subsequently noticed this in the roughly eight-year period between when he presented to the Academy and when his paper was published in the Miscellanea Berolinensia.
The Four Curves of Alexis Clairaut: Provenance of the Text
For the transcription of this text, “Quatre Problèmes sur de Nouvelles Courbes,” we worked with a digitized copy of Miscellanea Berolinensia, volume 4, on Google Books that had been digitized from an original copy held by Princeton University Library. We also consulted another original copy, located at the University of Illinois, to clarify any ambiguities in the digital version. The Illinois copy was also invaluable because Google’s digital version does not include the figures; they were printed on fold-out sheets, which were not unfolded by the digitizer.
The copy at Illinois contains a very ornate bookplate, ex libris C.S. Iordani, et amicorum [the book of C. S. Jordan and friends]. The bookplate depicts a well-stocked library with several men and angels. The Latin at the top and bottom are both from Virgil: the top, Dulces ante omnia musae [above all, the dear Muses], is from the Georgics; the bottom, Deus nobis haec otia fecit [God has granted us this rest], is from the Eclogues.

Figure 4: Bookplate as it appears in the University of Illinois copy.
The Rare Book & Manuscript Library, University of Illinois at Urbana Champaign.
We learn from Rzepka, Sosnowski, and Tylus (in [13]) that the book was from the library of Charles-Etienne Jordan. Jordan was born 27 August 1700 in Berlin and died on 24 May 1745. The family were Huguenot refuges, apparently originally from the province of Dauphiné, settling in Berlin. His father was a merchant, who desired for his son to take up an ecclesiastical career. Jordan studied philosophy and theology, before becoming a pastor at the French-speaking churches in Putzlow and later Prenzlau, both in the northwest of modern Germany, which was then the Kingdom of Prussia. In 1736 he entered the service of then-Prince Frederic II (later Frederick the Great). He was an avid collector of books. After his death, his collection seems to have been split up. Many of his works ended up in the the Royal Library of Berlin. The exact details of how this copy of Miscellanea Berolinensia came from Jordan’s collection to Illinois are currently unknown.
The reader may have wondered at this point if the mathematician Camille Jordan (1838–1922) was related to Charles-Etienne. This is in fact the case, though probably not directly. It seems that members of the family returned to France, where they lived in Lyon and the province of Dauphiné. The family in Lyon were merchants, from whom the orator Camille Jordan (1771–1821) descends. This Camille Jordan had a nephew, Alexis Jordan, who was a botanist. Alexis Jordan (1814–1897) was the first-cousin (oncle à la mode de Bretagne) of the mathematician Camille Jordan. For more information on the family and relevant biographical details, see [11, pp. x–xiv] and [1, pp. 255 et seq.].
The Four Curves of Alexis Clairaut: Editorial Conventions
French Transcription
In transcribing Clairaut’s text (pdf), we remained faithful to his sentence structure, grammar, and word choice. We did, however, modernize antiquated spellings and add accenting as appropriate for modern French. We also expanded abbreviations. The original spelling, accenting, or abbreviations are given in critical apparatus, which appear as a collection of footnotes on the French pages. The lines of the text are numbered for reference, but the reader should note that line numbers do not appear in the original text and do not correspond in any way to the lines of the original text.
For the mathematical content of the French transcription, we maintained the notation Clairaut chose as much as possible. For example, Clairaut often has expressions such as
√[\(xx + yy\)],
and we have preserved these as much as is possible with \(\LaTeX\).
The critical apparatus for the French consists of three groupings:
-
Group A: Textual. These footnotes indicate textual changes, such as a modernization of spelling or accenting. For example, the word “côtez” appears in the original text, but we have updated it to read “côtes”. The verb côtes appears in the main text, and the corresponding footnote reads 2 côtes ] côtez. The number corresponds to the line number on which the word occurs; the word preceding the bracket indicates the spelling in our edition; the word after the bracket indicates the spelling in the original.
-
Group B: Reading. These notes are intended to clarify the meaning of a word in French. For example, Clairaut uses the word “quarrant”. This is, however, an antiquated word; a modern equivalent would be the word “carrer” (“to square”).
-
Group C: Mathematical. These notes indicate corrections to the mathematical content. For example, Clairaut’s original text has \(x^{n+1}\) in a place where it should be \(x^{n+2}\). These notes also indicate issues with the diagrams, such as an omitted label in Clairaut’s original.
English Translation
We chose to not attempt a literal, word-for-word translation (pdf), and have instead taken some small liberties to give one with clearer meaning. For example, Clairaut employed a plethora of semicolons in his text. If we interpret them as periods, the result is a string of sentence fragments. If we interpret them as semicolons, it results in a massive run-on sentence. Accordingly, we have been flexible with sentence breaks, and have done so both to make the text readable and to remain true to what we think was Clairaut’s intent.
For mathematical notation in the English, we have used modern styling. For example, we replace Clairaut’s \(xx\) with \(x^2\) , and we render surds as square roots, e.g. \(\sqrt{x^2 + y^2}\) instead of √\(xx + yy\).
Notes in the English translation are of two varieties:
- Translation. These items comment on specific aspects of our translation.
- Mathematical. These items explicate mathematical details, such as intermediate steps not justified by Clairaut.
General Editorial Conventions
In both the English and French, we have taken the liberty of placing most of the mathematical notation on its own line. The source text prints them in-line, and this is often detrimental to the readability of complicated notation. Equations count as a new line for the purposes of line numbering, and each equation is numbered in the usual \(\LaTeX\) style.
The mathematical expressions are formatted in two ways. Points are given in “math bold” style, e.g. the point \(\mathbf{A}\) or the point \(\mathbf{n}\). Algebraic quantities are given in standard \(\LaTeX\) italics, e.g. \(x, y, a, m, n\). This was necessary in order to distinguish the points \(\mathbf{a}\) and \(\mathbf{n}\) from the algebraic quantities \(a\) and \(n\), as Clairaut used both throughout the paper. This is also advantageous because it distinguishes between the point \(\mathbf{a}\), the algebraic quantity \(a\), and the common French verb “a”, a conjugation of “avoir”.
The figures were created using GeoGebra, enabling the reader to manipulate the positions of some points. Clairaut’s curves are given in color (red or blue), and other lines are given in black. Some lines are dashed: often this is because Clairaut did so in his diagrams, but on a few occasions, we have made lines dashed so as not to distract from the more important parts of the figures. The coordinate system requires explanation: Clairaut oriented the \(x\) axis running vertically, and \(y\) axis running horizontally. In order to graph Clairaut’s curves, it was necessary to switch \(x\) and \(y\), since GeoGebra requires the modern standard coordinate system of \(x\) running horizontally and \(y\) vertically. We have not changed \(x\) and \(y\) in the text. If the reader desires to graph the curves themselves, e.g. with Mathematica or GeoGebra, it will be necessary to switch \(x\) and \(y\) as they appear in the text so that the graphs match the orientation used by Clairaut.
The Four Curves of Alexis Clairaut: Technical Notes
On the Finding of Mean Proportionals
The problem of finding a number of mean proportionals between two given segments has its origins in the Elements of Euclid. The case of one mean is easy. However, many mathematicians in the Greek period toiled over the problem of how to find two means. The case of two means is equivalent to the more famous problem of doubling the cube; namely, given a cube, to construct a new cube double in volume. Hippocrates of Chios (470–410 BCE) realized that this problem could be solved by finding the first of two mean proportionals between the volume of the original cube and the volume of the desired cube (generally double).
What Hippocrates realized is that, assuming \(\mathbf{A}\) and \(\mathbf{D}\) are the given magnitudes, then
\(\mathbf{A}\) : \(\mathbf{D}\) :: cube on \(\mathbf{A}\) : cube on \(\mathbf{B}\) iff \(\mathbf{A}\) : \(\mathbf{B}\) :: \(\mathbf{B}\) : \(\mathbf{C}\) :: \(\mathbf{C}\) : \(\mathbf{D}\).
Hence, if we let \(\mathbf{D}\) = 2 and \(\mathbf{A}\) = 1, then the cube with edge-length \(\mathbf{B}\) will have volume 2. The problem, then, is finding \(\mathbf{B}\). Eutocius of Ascalon (480–540) recorded a number of ancient solutions to this problem, which the reader can find in the original Greek in [5] or [7], or in English in either [6] or [12].
In the Elements, Euclid called this result by the name of triplicate ratio. He first defined duplicate ratio. If three magnitudes \(\mathbf{A}\), \(\mathbf{B}\), and \(\mathbf{C}\) are in continuous proportion, then \(\mathbf{B}\) is the mean proportional between \(\mathbf{A}\) and \(\mathbf{C}\), that is,
\(\mathbf{A}\) : \(\mathbf{B}\) :: \(\mathbf{B}\) : \(\mathbf{C}\).
Then \(\mathbf{A}\) has to \(\mathbf{C}\) the duplicate ratio of that which \(\mathbf{A}\) has to \(\mathbf{B}\). For Clairaut, this can be expressed as
\(\mathbf{A} : \mathbf{C} :: (\mathbf{A} : \mathbf{B})^2 :: \mathbf{A}^2 : \mathbf{B}^2\)
Similarly, if there are four magnitudes \(\mathbf{A}\), \(\mathbf{B}\), \(\mathbf{C}\), and \(\mathbf{D}\), then \(\mathbf{B}\) is the first of two means proportional between \(\mathbf{A}\) and \(\mathbf{D}\) (the second being \(\mathbf{C}\)). Then \(\mathbf{A}\) has to \(\mathbf{D}\) the triplicate ratio of that which \(\mathbf{A}\) has to \(\mathbf{B}\). Symbolically,
\(\mathbf{A} : \mathbf{C} :: (\mathbf{A} : \mathbf{B})^3 :: \mathbf{A}^3 : \mathbf{B}^3\)
Clairaut made use of the generalization of these concepts to any number of means. If there are magnitudes \(\mathbf{X}_0\), ..., \(\mathbf{X}_{n+1}\), then the term \(\mathbf{X}_1\) is the first of \(n\) means proportional between \(\mathbf{X}_0\) and \(\mathbf{X}_{n+1}\), and
\(\mathbf{X}_0 : \mathbf{X}_{n+1} :: \mathbf{X}_0^{n+1} : \mathbf{X}_1^{n+1}\) .
Here, the two given segments are \(\mathbf{CG}\) and \(\mathbf{CM}\); \(\mathbf{CF}\) is the first of \(n\) means proportional. Clairaut used this result to yield the equations for his generalized curves in each of the four problems below.
On the Translation of Genre
In our translation of Clairaut’s article, there was one mathematical term whose meaning was unclear: “genre”. Clairaut’s curves are fourth degree, which he calls “of the third genre”.
Possible translations of “genre” include “gender”, “genre”, and “genus”; we also investigated the possibility of “genre” translating to “degree” or “class”. We decided on “genre” for the following reasons. “Gender” would likely mean that the classification was binary, but this does not make sense given that Clairaut’s curves are, as he says, of the third genre. This can be seen in Problem III, point 1. “Genre” and “degree” are clearly not equivalent in the text, since, as we have said, his curves are of fourth degree but third genre.
“Genus” seemed another possibility to use as a translation. However, the word “genus” has a meaning in modern mathematics, both in topology and projective geometry, and it was not clear if Clairaut’s intended meaning matched the modern concept, despite the fact that his four curves are of the third genus (in the modern sense). This is because each of them is non-singular, and so the genus-degree formula
\(g = \frac{(d - 1)(d - 2)}{2}\)
gives \(g = 3\) when \(d = 4\). As we will see shortly, however, it is a coincidence that the genus of these curves matches the “genre” assigned by Clairaut.
D. E. Smith, in his edition of Descartes’ La Géométrie [3], translated “genre” as “class”. However, Descartes’ use of the word “genre” does not line up with Clairaut’s. Descartes organized curves into classes based on degree, with first and second degree curves (corresponding to lines and conic sections) being of the first class. Third and fourth degree curves are of the second class, etc. This clearly does not match Clairaut’s use, since under Descartes’ system, a fourth degree equation would be of the second class. The meaning of “genre” then must have changed between Descartes and Clairaut.
The answer comes from Guisnée’s book Application de l’algèbre à la géométrie. “Genre” means one less than the degree. We know from our Introduction that Clairaut studied from this very book only a few years prior to preparing the results of his article. We thus conclude that Clairaut’s sense of “genre” is the same as Guisnée’s. As for how to translate the word, we decided to simply use the English “genre”, and not “class”. This allows us to avoid mixing up Clairaut’s sense of “genre” with Descartes’, and our usage also will not tempt the reader into thinking of “class” in the modern sense as in \(C^{\infty}\).
Ultimately the word has no mathematical importance: since it is just one less than the degree, stating the genre does not add any information. It is important, though, in understanding how Clairaut, Guisnée, and other mathematicians of their time thought philosophically about the classification of algebraic curves.
The Four Curves of Alexis Clairaut: Conclusion
Again, we have prepared both a French transcription (pdf) and English translation (pdf) of “Quatre Problèmes sur de Nouvelles Courbes.” We hope that his paper has given you a window into Clairaut’s young genius; even today, it would be exceptional for a twelve-year-old to be able to read this work, much less produce it!
Many of the problems given by Clairaut would find themselves very much at home in a calculus classroom, either as interesting curves for implicit differentiation exercises, or for topics on integration. The curves could be taken out of context for this purpose. But pay attention to the reactions of the students: the exceptionally curious might like to see the fuller background. Do this especially for students who have (or want to) study French, and share it with your colleagues in French!
We certainly encourage the reader to also look at Descartes and perhaps even Guisnée. The ability for us to access these works and others through Google Books and Gallica was absolutely indispensable to the project. So many works are available digitally, and even in machine-searchable formats, that finding material inside a work is easy. We were fortunate to have the two eulogies pointing us to Guisnée, but a quick search for “genre” took us to the exact pages we needed.
The Four Curves of Alexis Clairaut: References
[1] Camille Jordan et Madame de Stael. Nouveaux Lundis (Ed. C. Lévy), vol. 12. Paris: P. Mouillot, 1884, pp. 255–336.
[2] Clairaut, A. Quatre Problèmes sur de Nouvelles Courbes. Miscellanea Berolinensia, vol. 4. Berlin: J. H. Rüdigeri, 1734, pp. 143–152.
[3] Descartes, R. The Geometry of René Descartes. 1637. English translation by D. E. Smith and M. L. Latham. Republished by Dover, 2012.
[4] Dugas, R. Éloge de Clairaut. Journal des Sçavans, (April 1766), pp. 191–194.
[5] Eutocius of Ascalon. Commentary on Archimedes’ On The Sphere and the Cylinder. In Archimedis Opera omnia, cum commentariis Eutocii (Ed. J. L. Heiberg), vol. 1. E codice Florentino recensuit. Leipzig: B. G. Tuebneri, 1880.
[6] Eutocius of Ascalon. Commentary on Archimedes’ On The Sphere and the Cylinder. In The Works of Archimedes: The Two Books On the Sphere and the Cylinder (Ed. R. Netz), vol. 1. Cambridge University Press, 2004.
[7] Eutocius of Ascalon. Commentary on Archimedes’ On The Sphere and the Cylinder. In Archimedis Opera omnia, cum commentariis Eutocii (Ed. J. L. Heiberg), vol. 1. E codice Florentino recensuit. Republished by Cambridge University Press, 2013.
[8] Grandjean de Fouchy, J.-P. Éloge de Clairaut. Histoires et Mèmoires de I'academie royale des sciences, Année 1765. Paris: Baudouin, Imprimeur de l'Institut National, 1768, pp. 144–159.
[9] Guisnée, Nicolas. Application de l’algebre à la géométrie. Paris, 1705.
[10] Itard, J. Clairaut, Alexis-Claude. In Dictionary of Scientific Biography (Ed. C. C. Gillespie). New York: Charles Scribner's Sons, 1971, vol. 3, pp. 281–286.
[11] Lebesgue, H. Notice sur la Vie et les Travaux de Camille Jordan. In Œuvres de Camille Jordan (Eds. R. Garnier and J. Dieudonné), vol. 4. Paris: Gauthier-Villars et Compagnie, 1964.
[12] McKinney, C. B. P. The Duplicators, Part I: Eutocius’ Collection of Cube Duplications. Convergence, vol. 13 (2016).
[13] Rzepka, A., Sosnowski, R., and Tylus, P. The history of the collection of Romance manuscripts from the former Preussische Staatsbibliothek zu Berlin. Faculty of Philology, Jagiellonian University of Kraków, 2011.
The Four Curves of Alexis Clairaut: Acknowledgments and About the Authors
Acknowledgements
Our work would not have been possible with the generous support of a number of individuals and institutions. They are:
-
The University of Illinois Rare Book and Manuscript Library, especially Tony Hynes, Caroline Szylowicz, and their student employees. We are especially indebted to them for the wonderful reproductions of the plates from the original book.
-
The Wabash College Department of Mathematics and Computer Science, for providing funding to support Jonathan and Taner as part of the project.
-
The Wabash College Media Center, especially Benjamin Cramer and Tu Nguyen, for their assistance in editing the photographs used in this article.
-
Google Books and Gallica (the latter run by the Bibliothèque nationale de France) for their digitization efforts. Many of the works cited and consulted would have otherwise been inaccessible. Additionally, having digital versions allowed us to clip out diagrams.
-
The two anonymous reviewers, whose keen eyes and masterful command of French have greatly improved this work and saved us from many embarrassing errors.
-
The editorial staff of Convergence for their assistance with bringing this project to a (long overdue) conclusion. And of course for their patience with Colin for being so slow to finish revisions!
About the Authors


Figures 5 and 6. Taner Kiral and Colin McKinney researching Clairaut at the Rare Book & Manuscript Library,
University of Illinois at Urbana Champaign; Jonathan Murdock. Photos supplied by the authors.
Colin McKinney is an associate professor of mathematics and computer science at Wabash College, and holds the rank of Captain in the United Federation of Planets’ Starfleet. He appreciates good music, good food, good math, good Greek, and good whiskey . . . preferably all at the same time. He enjoys spending time cooking and hanging out with his lovable Cairn Terrier, Mia.
Taner Kiral graduated from Wabash College in 2017 with a Bachelor of Arts in Pure and Computational Mathematics and a minor in Physics. Taner presented his work on Clairaut to the 2016 Indiana Undergraduate Math Research Conference at IUPUI Department of Mathematical Sciences, the 2017 Joint Mathematics Meetings Undergraduate Presentation Sessions, and the 2017 Wabash College Undergraduate Research Student Celebration. This work won the 2017 Wedgeworth Prize as well as the 2017 Lilly Library Award, both awarded by Wabash College. He works as a Data Engineer for Amazon and enjoys playing the Kalimba, hanging out with his dog, Lilo, and spending time with his girlfriend.
Jonathan Murdock graduated from Wabash College in 2019 with a Bachelor of Arts in Financial Economics and a minor in French. Jonathan’s work on Clairaut has been featured at the 2016 Indiana Undergraduate Math Research Conference at the IUPUI Department of Mathematical Sciences, the 2017 Joint Mathematics Meetings Undergraduate Presentation Sessions, and the 2017 Wabash College Undergraduate Research Student Celebration. He now works as a Global HR Solutions Associate in the Advisory practice for PricewaterhouseCoopers. He lives in Philadelphia, PA, with his spouse-equivalent, Emma, and their two cats, Reece and Matilda, all of whom he loves very much.