Mathematical Mysteries of Rapa Nui with Classroom Activities
One of the most remote inhabited locations in the world, the island Rapa Nui, also known as Easter Island, is shrouded in mysteries. When was it inhabited, by whom, and how did they survive the journey? Why were the large moai statues carved and how were they transported from the Rano Raraku quarry to the ahu platforms erected throughout the island? In this paper, after a brief introduction to Rapa Nui, we take a look at three mysteries: the partially undeciphered script called Rongorongo, the geometrical shape of the stone foundations of ancient houses called hare paenga, and the question of whether mathematics could have been used in laying out the foundations of those houses. We also share four classroom-ready student activities based on the mysteries surrounding the hare paenga.

Figure 1. Archaeological remains of a hare paenga, July 2019.
Except as noted, all photos in the article were taken by the authors.
Nota de las editoras: Para acceder a una versión en español de este artículo, haga clic aquí.
Mathematical Mysteries of Rapa Nui with Classroom Activities: Introduction
E ono kope o ruŋa: e hā taŋata, e tahi vi’e, ‘e he poki e tahi.
There were six people on board: four men, one woman, and one child. [Pakomio Ika 1984]
Formed by now inactive volcanic activity, Rapa Nui, or Easter Island as it became known, lies more than 2,200 miles off the Chilean coast and 1,300 miles from the nearest inhabited land, Pitcairn Island. Rapa Nui also sits at the southeasternmost point of the Polynesian Triangle. The island entered written history on Easter Sunday, April 5, 1722, when it was sighted by a Dutch fleet commanded by Jacob Roggeveen. The island was again visited in 1770 by a Spanish expedition led by Don Felipe González, followed by James Cook in 1774 and Count La Pérouse in 1786.
The name Rapa Nui is used to name both the island and its people. The language of the Rapa Nui people is Rapanui, meaning “great Rapa.” The meaning of the word "Rapa" is unknown; however, Rapa is the name of the southernmost island in French Polynesia [Kieviet 2017, 1]. Sources do not agree about the actual number of speakers of Rapanui, with estimates varying between 1,000 and 2,500 speakers.

Figure 2. Ximena Catepillán and Cynthia Huffman on Rapa Nui in July 2019.
We visited the island in July 2019 with a group led by archaeologist Dr. Edwin Barnhart from Ancient Explorations. The group included three mapping experts from Tukuh Technologies, a tribally-owned business located in Kansas City, MO. The mapping was conducted with two fixed-wing unmanned aircraft systems (UAS), commonly known as drones. The drones captured high-resolution orthoimagery of the archaeological sites. The laser beams of LiDAR technology (Light Detection and Ranging) were used to provide 3-D point cloud data of some of the caves on the island.


Figure 3. (Left) Ximena Catepillán launching a fixed-wing drone for photogrammetry of an area of the island.
(Right) Cynthia Huffman wearing a 50-lb $250,000 backpack with LiDAR technology.
After the trip, participants (including Drs. Catepillán and Huffman) were allowed to assist the team from Tukuh Technologies in locating archaeological features from the drone images. Below is a screenshot of the identification work in progress.
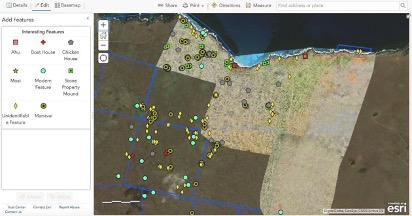
Figure 4. Example of identifying and mapping archaeological features. Courtesy of Tukuh Technologies, LLC.
Although Rapa Nui is famous for its monumental statues—or moai—it also has many lava tube caves with a great number of petroglyphs, and some pictographs, displaying a variety of motifs. In fact, Rapa Nui has one of the richest collections of such rock art in Polynesia. The cave Ana O Keke (Cave of the Virgins) was one of the sites visited by the surveyors and members of our group. This cave, whose small entrance borders a cliff, is seldom visited by tourists because of its difficult and dangerous access. It is located at the northeast end of the Poike volcano, on the east side of Rapa Nui, and it has a panel of petroglyphs on the right side of its entrance.

Figure 5. Entrance panel at Ana O Keke. Photo by Robert Tidwell.
The language of the Rapanui belongs to the family of Eastern Polynesian languages, a branch of the Austronesian languages. According to linguists, the first peoples arrived in approximately 400 CE. However, archaeologists date their arrival between 700 and 800 CE, although they agree the peoples quite possibly originated from East Polynesia. The Rapanui number system is decimal and almost identical to the Tahitian number system.
Mathematical Mysteries of Rapa Nui with Classroom Activities: Mathematical Mystery 1 – Rongorongo
The first mystery we will discuss is the unique form of writing, called Rongorongo, that was used by the sacred people in Rapa Nui. When slave traders from Peru abducted or killed nearly half the population of Rapa Nui in 1862, the ability to read Rongorongo was lost. It remains one of the partially undeciphered scripts in the world.
Fewer than 30 objects containing Rongorongo writing—mostly wooden tablets—have been discovered. The Rongorongo characters appear in lines, with alternating orientation. One theory is that two facing people read from the tablet; another is that the tablet could have been read by one person and turned when the end of the line was reached. The tablets are thought to have been used during special ceremonies by a few elite men, called rongorongo men or tangata rongorongo [Métraux 1971, 390–391; Routledge 1920, 245–246].
In 1958, Thomas Barthel published a book with lunar calendar information included on a Rongorongo tablet called the Mamari [Barthel 1958]. The figure below shows the lunar calendar glyphs found on the Mamari tablet. Combinations of these glyphs were used to compose the lunar month.

Figure 6. Drawings of Rongorongo lunar calendar glyphs, based on descriptions in Barthel 1958.
In 1990 Chile returned to democracy when Patricio Aylwin was democratically elected to the presidency after 17 years of dictatorship under Augusto Pinochet. President Aylwin began instituting various reforms in response to protests from indigenous groups, including the Rapanui. These included, among others, initiatives to grant the groups constitutional recognition and to increase local control over land and national resources [Baartmans 2012–2013, 12].
It was during those years that Ximena’s uncle, Jorge Catepillán, who was the Director of Business at Corporación de Fomento de la Producción (CORFO), a position given to him by President Aylwin, traveled with a governmental commission to Rapa Nui representing CORFO. CORFO is a national production development corporation; the Society of Agriculture & Services of Rapa Nui (SASIPA) is part of CORFO and owned 40% of the island until the early 2010s [Delsing 2015, 246].
A replica of a Rongorongo tablet was given to Jorge Catepillán as a present by an agricultural engineer and friend who had been living on Rapa Nui for many years. Both sides of the tablet can be seen below. Lunar calendar glyphs are highlighted on the bottom image.

Figure 7. Rongorongo tablet given to Jorge Catepillán.
Mathematical Mysteries of Rapa Nui with Classroom Activities: Background on the Hare Paenga (Boat Houses)
Before analyzing the next two mysteries, some background knowledge will be helpful. Archaeological objects called paenga can be found throughout Rapa Nui. These basalt curbstones once formed foundations of thatched houses called hare paenga or “boat houses”, which were so named since they looked like overturned boats. Holes in the paenga stones held poles that were tied together and then covered with thatch. A low door would be in the center of one of the longer sides of the boat house, which opened out to a stone patio. People slept “parallel to the long axis of the house, the head being towards the door; the old people were in the centre in couples, and the younger ones in the ends” [Routledge 1920, 200].



Figure 8. Three views of dressed paenga stones.


Figure 9. Exterior and interior of replica hare paenga; (Right) the inside shows the poles and thatching as well as Catepillán’s son, Sebastian.


Figure 10. (Left) Cutaway view of replica hare paenga revealing the foundation. (Right) Ximena Catepillán exiting a replica hare paenga.
The dressed paenga stones were reused throughout the years. Sometimes new holes were made and the stones were reused for another hare paenga. Others were reused in construction projects such as ahu platforms for moai, terraces, and well linings. Paenga were even “seized upon as booty in enemy raids” [Routledge 1920, 199]. More recently, during the first half of the 20th century, when most of the island was used for sheep farming, the stones were used in the stone walls that were constructed throughout the island.

Figure 11. Curbstones (paenga) reused to form an earth oven.
Mathematical Mysteries of Rapa Nui with Classroom Activities: Mathematical Mystery 2 – Geometry of Hare Paenga (Boat House) Foundations
Even with all the reuse of the paenga stones, surviving ruins of complete or near-complete hare paenga foundations still exist. Within the literature, the foundations of the Rapanui hare paenga are said to be elliptical. However, at first glance in person, the ruins of a hare paenga looked too pointed on the ends and too straight on the sides to be an ellipse.

Figure 12. Ximena Catepillán checking the orientation of the remains of a hare paenga.
Nevertheless, after investigating with GeoGebra and Desmos, we discovered that it is possible to fit an ellipse to the shape of a stone foundation with the foci of the ellipse close to the ends of the major axis.
The GeoGebra applet below demonstrates fitting an ellipse to the remains of a hare paenga stone foundation. By moving points on the ellipse in the bottom center of the applet, in particular the magenta point that controls the minor axis of the ellipse and the red point which is one of the foci, one can adjust to get the corresponding ellipse on the picture in the upper left to match up with the archaeological ruins. Moving the green point traces out the ellipse. Watching the sum above the “Reset” button, while moving the green point, dynamically demonstrates the definition of the ellipse; namely, that the sum of the distances from a point on the ellipse to each foci is a constant.
We were also allowed access to some images of hare paenga obtained by Tukuh Technologies during their mapping. We used GeoGebra to fit ellipses to the images. (See the student activity "Curve Fitting Applied to Rapa Nui Stone Foundations" for the step-by-step procedure used.)


Figure 13. Images of hare paenga foundations. Courtesy of Tukuh Technologies, LLC.

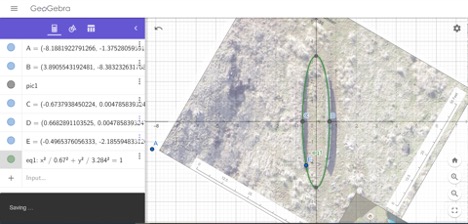
Figure 14. Screenshots of results from using GeoGebra to fit an ellipse to the ruins.
Mathematical Mysteries of Rapa Nui with Classroom Activities: Mathematical Mystery 3 – How Were the Hare Paenga Foundations Laid Out?
In addition to fitting ellipses over the hare paenga images with Desmos and GeoGebra, we analyzed twelve of the Tukuh Technologies drone images using rough measurements of the major and minor axes of these hare paenga remains.
| \(2a\) in feet | \(a\) in feet | \(b\) in feet | \(c\) in feet | \(a-c\) in feet | \(a-c\) in inches |
| 37.50 | 18.75 | 3.125 | 18.48775 | 0.262251 | 3.147008 |
| 37.50 | 18.75 | 3.125 | 18.48775 | 0.262251 | 3.147008 |
| 37.50 | 18.75 | 2.604167 | 18.56827 | 0.181726 | 2.180707 |
| 45.83 | 22.91667 | 3.125 | 22.7026 | 0.214068 | 2.568816 |
| 37.50 | 18.75 | 3.645833 | 18.39213 | 0.357871 | 4.294455 |
| 40.54 | 20.27027 | 3.716216 | 19.92671 | 0.343565 | 4.122777 |
| 33.33 | 16.66667 | 2.864583 | 16.41865 | 0.248021 | 2.976247 |
| 32.29 | 16.14583 | 2.864583 | 15.88969 | 0.256148 | 3.073777 |
| 30.21 | 15.10417 | 2.604167 | 14.87798 | 0.226191 | 2.714289 |
| 33.33 | 16.66667 | 2.604167 | 16.46196 | 0.204708 | 2.456492 |
| 35.94 | 17.96875 | 2.864583 | 17.73894 | 0.229806 | 2.75767 |
| 40.63 | 20.3125 | 3.645833 | 19.98263 | 0.329869 | 3.958424 |
Averages
| \(2a\) in feet | \(a\) in feet | \(b\) in feet | \(c\) in feet | \(a-c\) in feet | \(a-c\) in inches |
| 36.84 | 18.42 | 3.07 | 18.16 | 0.26 | 3.12 |
These measurements were similar to ones found from fieldwork on Rapa Nui in 1968–1969: “hare paenga in the survey area were of average size, corresponding to Métraux’s [1971, 200] observations of general house dimensions—10 to 15 meters long and 1.5 to 2 meters broad. The smallest was 4.8 x 1.3 meters and the largest more than 40 meters long as calculated from the length of the house pavement” [McCoy 1976, 50].
Notice the last column of the table above. The value \(a-c\) is the distance between a focus and the nearest end of the major axis. For the examples in the table, this value is roughly 3 to 4 inches, which could correspond to the width of a hand or 3–4 fingers. Although there is no known surviving evidence of how the hare paenga foundations were laid out, one method that would work would be based on the definition of an ellipse using rope (with length equal to the desired length of the boat house), 2 stakes or poles (set at the foci about a hands-width in from the ends of the major axes), and a stick for marking the ellipse in the dirt. (See the corresponding class activities.) The video below demonstrates how the foundations could have been laid out using the definition of an ellipse.
Even though we don’t know exactly how the Rapanui laid out the foundations, there is evidence that they used rope or string for measurements. The following quote is from an expedition to Easter Island in 1786: “The care they took to measure our vessel convinced me, that they had not contemplated on arts with stupidity. They examined our cables, our anchors, our compass, and our steering wheel; and in the evening they returned with a string to take their measure over again” [La Pérouse 1798, 328, emphasis added].
It is not known how soon after Rapa Nui was inhabited that the people started building hare paenga, but the use appears to have been discontinued by the mid-19th century [Métraux 1971, 196, 200]. In her expedition of 1910, Katherine Routledge met older people, many of whom “were born and brought up in these houses, which are known as ‘hare paenga’” [Routledge 1920, 200]. It should be mentioned that the hare paenga were not the only type of houses used in the past on Rapa Nui. In fact, it is thought that only a select few had a hare paenga in which to sleep or to get out of the rain. Others may have lived in thatched huts without foundations. Caves and rock shelters of various sizes were also used.


Figure 15. Subterranean dwelling and stone houses at Orongo, a ceremonial village at the southwestern tip of Rapa Nui.


Figure 16. Ana Te Pahu—once inhabited and the largest cavern complex on the island.
In some locations the wind is too strong to make a thatched dwelling practical. Stone elliptical houses were constructed, which Métraux [1971, 204] suggests were modeled after the hare paenga. The measurements of one such house [La Perouse 1798, 192] were 26 feet for the major axis and 6 feet for the minor axis, giving a distance of a little over 4 inches between an end of the major axis and a focus, similar to the hare paenga discussed above.
Mathematical Mysteries of Rapa Nui with Classroom Activities: The Activities
Four classroom-ready activities based on the explorations in this article are provided below, as links to PDF files.
This worksheet activity (pdf) is appropriate for secondary students in a class studying conic sections or students in a college algebra class. The first part of the activity gives an algebraic review of ellipses with exercises while the second part finds the equation of an ellipse corresponding to a Rapanui boat house foundation.
Activity 2: Outdoor Activity Modeling an Easter Island boat house foundation with an ellipse
This outdoor activity (pdf) would fit in with a secondary or college class studying ellipses and gives students a hands-on application of the definition of an ellipse.
Activity 3: Indoor Activity Constructing a Scale Model of an Easter Island boat house foundation with an ellipse
This indoor activity (pdf) is a modification of Activity 2 for use inside the classroom. Students are asked to find an appropriate scale and then construct a scale model of a Rapanui boat house based on the definition of an ellipse. Activities 3 and 2 could be combined by having students first construct a scale model (Activity 3) and then construct a full-scale model outside (Activity 2).
Activity 4: Curve Fitting Applied to Rapa Nui Stone Foundations
This curve fitting activity (pdf) can be used as a teacher demonstration or completed by students, either individually or in groups. GeoGebra is used to fit an ellipse to a drone image of a hare paenga foundation.
Mathematical Mysteries of Rapa Nui with Classroom Activities: Conclusion
The questions that motivated the study that we undertook in connection with our trip to Rapa Nui were: Are the stone bases of the hare paengas elliptical? Did the Rapanui use the two-foci technique to lay out the hare paengas? And, is there any mathematics embedded in the Rongorongo script? We have answered the first question in the paper, thanks in part to confirmation provided by studying the imagery collected via drones and LiDAR technology. However, the answer to the second remains a mathematical mystery. Finding a lunar calendar description on some of the Rongorongo tablets provides a first step toward answering the third question, but much study remains to completely decipher the tablets.
One of the difficulties in answering the second question is the limited information available, since today only a small number of hare paenga survive. Métraux [1971, 195] believed that while hare paengas were common, stone-based hare paengas were not as common and were a reflection of wealth and status. Sadly, many of the hare paenga stone bases were reused later in the construction of walls, stone houses, and other dwellings. In the picture below, depicting the interior of an underground shelter called ana kionga or hare kionga, the reader can see how hare paenga bases were used to build an interior wall [McCoy 1976, 38].

Figure 17. Structure made from reused paenga stones depicted in McCoy 1976.
In 1916, Edwin Ferdon brought attention to certain resemblances between the floor plan of the Orongo houses and the hare paenga. The Orongo houses—built in the ceremonial village of Orongo at the southwestern tip of Rapa Nui—were permanent structures to which the high-ranking participants in the ceremonies could return each year. It is believed that forest depletion was the cause of the appearance of this type of stone house construction [McCoy 1976, 151].
It is quite frustrating to read how little attention and funds have been dedicated to the restoration and preservation of the archaeological sites on the island. Moreover, some of the restoration work has not been done in a way that preserves its authenticity [Ramirez 2016, 138–141]. In the 1960s, the construction of the first airport on the island used bulldozers that removed thousands of tons of topsoil containing archaeological material including moai pieces, house foundations, and a stone figure believed to include astronomical elements [Ramirez 2004, 493]. We encourage readers to join us in identifying and supporting organizations working to protect Rapa Nui’s archaeological and ecological heritage. Furthermore, we hope that some readers of this article might become—or teach the students who become—the archaeologists, anthropologists, and mathematicians who solve the mathematical mysteries of this unique island!
Mathematical Mysteries of Rapa Nui with Classroom Activities: References
Baartmans, Chloe. 2012–2013. Rapa Nui: the struggle for indigenous land rights on Easter Island. MA Thesis, Tilburg Law School, The Netherlands.
Barthel, Thomas. 1958. Grundlagen zur Entzifferung der Osterinselschrift. Hamburg: Cram, de Gruyter.
Delsing, Riet. 2015. Articulating Rapa Nui: Polynesian Cultural Politics in a Latin American Nation-State. University of Hawai‘i Press.
Desmos Graphing Calculator. Accessed 14 December 2020. https://www.desmos.com/calculator.
Ferdon, Edwin N., Jr. 1961a. Easter Island house types. In Archaeology of Easter Island. Reports of the Norwegian Archaeological Expedition to Easter Island and the East Pacific, edited by T. Heyerdahl & E.N. Ferdon, vol. 1, 329–338. Santa Fe: Monographs of the School of American Research and the Museum of New Mexico.
——. 1961b. Stone houses in the terraces of site E-21. In Archaeology of Easter Island. Reports of the Norwegian Archaeological Expedition to Easter Island and the East Pacific, edited by T. Heyerdahl & E.N. Ferdon, vol. 1, 313–321. Santa Fe: Monographs of the School of American Research and the Museum of New Mexico.
GeoGebra. Accessed 14 December 2020. https://www.geogebra.org/.
Kieviet, Paulus. 2017. A Grammar of Rapa Nui. Vol. 12, Studies in Diversity Linguistics. Berlin: Language Science Press.
La Pérouse, Jean-François, comte de Galaup, L. A. Milét-Mureau, and L. Destouff. 1798. The voyage of La Pérouse round the world, in the years 1785, 1786, 1787, and 1788, with the nautical tables. 3 vol. London: Printed for John Stockdale.
McCoy, Patrick Carlton. 1976. Easter Island Settlement Patterns in the Late Prehistoric and Protohistoric Periods. Bulletin 5, Easter Island Committee. New York: International Fund for Monuments, Inc.
Métraux, Alfred. 1971. Ethnology of Easter Island. Bernice P. Bishop Museum Bulletin 160. Honolulu, Hawaii. (Orig. pub. 1940.)
Omniglot: the online encyclopedia of writing systems and languages. Accessed 14 December 2020. omniglot.com/writing/rongorongo.htm.
Pakomio Ika, Toribio. 1984. He via he aŋa o Eugenio Eyraud (Vida y trabajo de Eugenio Eyraud). Isla de Pascua: Taller de Escritores Rapa Nui. Universidad Católica de Valparaíso e Instituto Lingüístico de Verano.
Ramírez Aliaga, José Miguel. 2004. Manejo del Recurso Arqueológico en Rapa Nui: Teoría y Realidad. Chungará (Arica) 36, supp. 1: 189–197. https://dx.doi.org/10.4067/S0717-73562004000300049.
Ramirez Aliaga, Jose Miguel. 2016. Reconstruyendo la Aldea Ceremonial de Orongo: El Dilema de la Autenticidad. MP Thesis, Universidad de Valparaíso, Chile.
Routledge, Katherine. 1920. The mystery of easter island: The story of an expedition. London: Printed for the author by Hazell, Watson and Viney.
Tukuh Technologies. Accessed 14 December 2020. https://www.tukuh.com.
Mathematical Mysteries of Rapa Nui with Classroom Activities: Acknowledgements and About the Authors
Acknowledgements
We would like to express our special thanks to Robert Tidwell, an anthropologist who traveled with us to Rapa Nui and provided excellent sources and advice that facilitated the writing of this article.
We thank the referees and editors for the careful and insightful review of our article which led to significant improvements to our submission.
About the Authors
Ximena Catepillán recently retired from the Department of Mathematics at Millersville University of Pennsylvania. She chaired the MAA EPaDel Section between 2017 and 2019. Ximena has indigenous roots in South America and is passionate about the mathematics of the pre-Columbian Americas.
Cynthia J. Huffman is a University Professor in the Department of Mathematics at Pittsburg State University. She has always been interested in history of mathematics but her interest was especially sparked by participation in several of the MAA Study Tours. Her research areas include computational commutative algebra and history of mathematics. Dr. Huffman is a handbell soloist and has a black belt in Chinese Kenpo karate.
Scott Thuong is an Associate Professor in the Department of Mathematics at Pittsburg State University. His research areas include topology, geometry, and the history of mathematics. Dr. Thuong enjoys spending time with his two basset hounds and engaging in a good game of table tennis.