Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course

Figure 1. Ada Lovelace (1815–1852) in 1836, by Margaret Sarah Carpenter. Government Art Collection.
The name of Ada Lovelace has long been well known among mathematicians and computer scientists. Many will have seen her described as ‘the first computer programmer’—indeed, if you are old enough, you may have even encountered the programming language, Ada, that was named in her honor in 1979. Early computing pioneers acknowledged her work in the 1940s and 1950s, with Alan Turing commenting, for example, on her thoughts on artificial intelligence. Today, she is one of the few mathematical scientists who could be described as a ‘household name’ and is arguably more famous among the general public than any other female mathematician in history.
In her own lifetime she was also famous, but for a completely different reason. Augusta Ada King, Countess of Lovelace (1815–1852) was the only legitimate child of the poet Lord Byron, and, in common with the offspring of some dead celebrities today, she lived a privileged but somewhat isolated lifestyle with her every move watched and scrutinized by society. Her present-day fame stems from a 66-page paper she published in 1843, containing an account of a machine called the analytical engine [Lovelace 1843]. Designed by the famous Victorian mathematician, inventor, and polymath Charles Babbage in the 1830s, had it ever been built, this theoretical device would have been the world’s first general purpose computer—100 years before the dawn of the modern computer age.
Lovelace’s 1843 paper contained seven lengthy appendices, or ‘Notes’, with the last one, Note G, providing her chief claim to fame. In it, she outlined an iterative process by which Babbage’s machine, via a series of steps, could compute Bernoulli numbers, an irregular sequence of rational numbers, highly useful in number theory and analysis. Using the fact that these numbers are the coefficients of the \(\frac{x^n}{n!}\) terms in the infinite series expansion
\[\frac{x}{e^x-1}=\sum_{n=0}^{\infty} B_n \frac{x^n}{n!}\]
she devised an algorithm that could generate each Bernoulli number in turn. This is what has gone down in history as the world’s ‘first computer program’—although what she published was actually more akin to a modern-day execution trace than a program. (See Figure 2.)
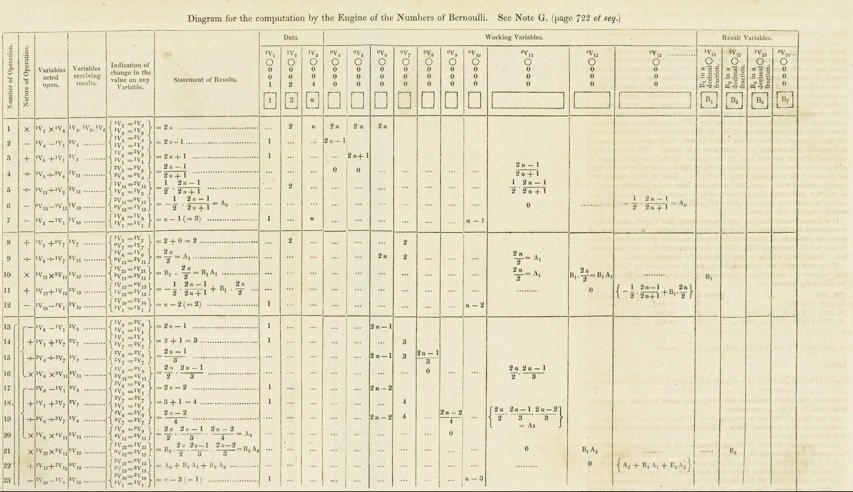
Figure 2. Diagram from Ada Lovelace’s 1843 paper showing the step-by-step procedure by which Bernoulli numbers could, in theory, be calculated by Babbage’s analytical engine [Lovelace 1843].
Over the years, the extent to which this algorithm was due to Lovelace has been hotly debated. For example, in his 1864 autobiography, Babbage noted that he had provided Lovelace with the underlying algebra for it. Nevertheless, he also recalled that she had ‘detected a grave mistake which I had made in the process’ [Babbage 1864, 136], which has led some to credit her not as the world’s first programmer, but rather as the ‘first debugger’! Originality aside, however, the fact remains that in order to explain the process of calculating Bernoulli numbers in her 1843 paper, Lovelace would have needed an understanding of the mathematics underlying the procedure. And this was by no means trivial, since the algebra involved would largely have been beyond the capability of anyone who had not had some kind of university-level tuition in mathematics. In the mid-19th century, no such education was formally available to women.
Yet it turns out that shortly before beginning work on her famous paper, Lovelace did manage to learn advanced mathematics from an unexpected source. For a period of approximately eighteen months, from the summer of 1840 to the winter of 1841/42, she took what would now be called a correspondence course with the British mathematician and logician, Augustus De Morgan (1806–1871). During this period, De Morgan introduced Lovelace to a substantial portion of what then comprised an undergraduate course in mathematics. From basic algebra and trigonometry, she progressed through logarithms and functions to the course’s principal component and the subject to which she devoted the most attention: calculus. The correspondence between Lovelace and De Morgan survives in the form of sixty-six letters from this period, now housed in the Bodleian Library in Oxford.
To shed more light on the mathematics Ada Lovelace actually studied in order to produce her famous paper of 1843, a recent research project, undertaken by Chris Hollings, Ursula Martin and myself, looked in detail at these surviving letters. Our research resulted in two papers, [Hollings et al. 2017a] and [Hollings et al. 2017b], and an expository book [Hollings, et al. 2018], differing from previous studies in concentrating specifically on the details of the actual mathematics that Lovelace studied with De Morgan. We found that she was an extremely keen and capable student, although certainly prone to the usual beginner’s mistakes and misapprehensions. Not surprisingly, these errors featured prominently in her letters to De Morgan, since she would not have wasted time (and paper) telling him what she already understood, but would naturally have written more to ask questions about material on which she needed further explanation and help.
It is these misunderstandings as highlighted by Lovelace in her correspondence with De Morgan that form the basis of this article. I have selected ten particular problems (homework exercises, if you like) on which Lovelace encountered difficulties at some point in her course of study; they mainly concern calculus, although some are more foundational, involving limits or basic algebra. As we will see, some of these problems appear almost trivial, while others are more sophisticated. But they all underscore common sources of confusion that still plague mathematics students and their teachers today. For this reason, they provide excellent templates for exercises that may be used in the classroom by students and teachers alike. Regardless of the level of the reader’s mathematical expertise, what emerges irrefutably from looking at all of these problems, together with Lovelace’s flawed attempts to solve them, is the comforting notion that even the most famous mathematicians make mistakes.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Lovelace’s Early Mathematical Education
Ada’s earliest introduction to mathematics instruction appears to have occurred around the age of five. A notebook kept by her governess, Miss Lamont, records that she ‘Commenced giving instructions to Miss Byron’ in May 1821. As Miss Lamont reported to Ada’s mother Lady Byron: ‘The first trial was in arithmetic. She adds up sums of five or six rows of figures, with accuracy; she is deliberate and correct in the process, and takes an interest in the performance’ [LB 118, item 5, 14 May 1821, f. 2r]. By the age of ten, Ada had been introduced to more advanced arithmetical techniques, such as the so-called Rule of Three, as illustrated in a letter to her mother, in which she wrote:
I have been puzzling hard at a sum in the rule of three which I could not do, the question is “If 750 men are allowed 22500 rations of bread per month, how many rations will a garrison of 1200 men require"?’ [LB 41, 1 June 1826, ff. 27r-27v].

Figure 3. Page from John Bonnycastle’s An Introduction to Arithmetic (1810) featuring Ada’s Rule of Three problem.
This type of problem, while relatively trivial today, was considered quite challenging at the time and was very common in 18th- and 19th-century mathematical textbooks. It was also considered to be a branch of arithmetic, whereas today it would be dealt with purely algebraically. Given three known numbers, \(a\), \(b\), and \(c\), the Rule of Three says that, if \[\frac{a}{b}=\frac{c}{x},\] then \[x=\frac{bc}{a} .\]
As can be seen from the extract from a contemporary 19th-century textbook above, the answer to Ada’s problem is 36,000 rations of bread. You will find a fuller explanation in the Solutions section of this article.
From this and other letters between mother and daughter, it would appear that Lady Byron was partly responsible for some of Ada’s initial education in mathematics, as she had herself received tuition in mathematics and science in her childhood, which was unusual for young ladies at the time. In particular, we see that she corrected her 13-year-old daughter’s misunderstandings concerning order of operations, from a passage in which Ada notes that (5×2)+(3×4)=22, and not 52 as she had previously believed:
I had not till Mama showed me, understood the sums where both multiplication and addition signs were used, in consequence of which the former examples must have been wrong, as I thought they were as follows: 5×2=10 to which add 3 = 13 which multiplied by 4 gives 52, instead of 5×2=10 to which add 3×4=12 [LB 175, 10 Feb. 1829, f. 176r].
By the age of 18, Ada was receiving informal guidance on her mathematical studies from an old family friend, Dr. William King, who had graduated from Cambridge a quarter of a century before. At his suggestion, she began working through Euclid’s Elements, writing to him that she was covering about ‘four new propositions a day, and go[ing] over some of the old ones. I expect now to finish the 1st book in less than a week’ [LB 172, 24 March 1834, f. 131r]. Before long, she was conjecturing her own variation of the Pythagorean theorem:
Can it be proved . . . that equilateral triangles being constructed on the sides of a right angled triangle, and also one on the hypotenuse, the sum of the triangles on the sides is equal to the triangle on the hypotenuse? . . . It strikes me that it ought to be as demonstrable as when the figures are four-sided & equilateral. [LB 172, Ada Byron to Dr King, 13 April 1834, f. 132r]
(You can see a sketch of roughly what she had in mind here.) But Dr. King was long out of practice with this sort of mathematics and unable to help her: ‘You will soon puzzle me in your studies,’ he replied [LB 172, 24 April 1834, f. 133r]. In just a few weeks, Ada had reached the bounds of her tutor’s expertise.
Around the time of her marriage to William, the 8th Lord King (who became the Earl of Lovelace in 1838), Ada turned for mathematical assistance to a new friend, Mary Somerville (1780–1872). In addition to being a respected and well-known scientific author, Somerville was acquainted with more up-to-date analytical methods, then comparatively new to British mathematics. By 1835, shortly after her marriage, Ada was reporting to Somerville that her mathematical reading had progressed to trigonometry and algebra: ‘I now read Mathematics every day & am occupied in Trigonometry & in preliminaries to Cubic & Biquadratic Equations. So you see that matrimony has by no means lessened my taste for those pursuits, nor my determination to carry them on...’ [Somerville Papers, Dep. c.367, Folder MSBY-3, 1 Nov. 1835, f. 55v].

Figure 4. Mary Somerville (1780–1872) in 1834, by Thomas Phillips. National Galleries Scotland.
But despite this apparent progress, her correspondence with Mary Somerville reveals significant gaps in the mathematical knowledge and abilities of the twenty-year-old Ada. In the same letter of 1835, she recounted a difficulty she was experiencing in trigonometry, namely to use the addition formulae
\[\sin(a+b)=\frac{\sin a \cos b+\sin b\cos a}{R}\]
\[\cos(a+b)=\frac{\cos a \cos b - \sin a\sin b}{R}\]
to derive expressions for \(\sin (a-b)\) and \(\cos (a-b)\). Of course, as Somerville was able to tell her, since \(\sin(-b) = - \sin \)b and \(\cos(-b)=\cos b\), the solution was simply a matter of substituting \(-b\) for \(b\) in the above formulae [LB 174, 8 Nov. 1835, ff. 29r-29v]. (Note that the use of a general radius of length R not necessarily equal to 1, such that \(sin^2 x+cos^2 x=R^2\), was not uncommon in trigonometry textbooks at this time.)
But the matter did not end there. Two weeks later, Ada was asking a similar, and only slightly harder Trigonometry Problem, namely, how to use
Once again, Somerville was able to resolve the difficulty in a few lines. If you wish to see how she solved the problem, click here.

Figure 5. Extract from the translation of Legendre’s Elements of Geometry and Trigonometry
published by David Brewster (1822), with which Ada Lovelace had difficulty.
Between 1836 and 1839, Ada gave birth to three children, which interrupted her mathematical studies somewhat, but in late 1839, after the birth of her third child, she began actively looking for a new tutor. By the summer of 1840, she could report to her mother that a suitable tutor had been found and her mathematical studies were once more underway. That tutor was Augustus De Morgan.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Augustus De Morgan and Mathematics at UCL
Augustus De Morgan was the founding professor of mathematics at University College London (UCL), where he had been appointed in 1828 at the age of only 21 [Rice 1997]. An intriguing character of high intellect, De Morgan was a prolific writer on all areas of mathematics, publishing numerous research papers, largely on algebra and logic, as well as on mathematical pedagogy [Rice 1999] and the history of mathematics [Rice 1996]. Unlike professorships at Oxford or Cambridge at this time, De Morgan’s post at UCL demanded a substantial amount of undergraduate teaching, but being deeply committed to education, he did not limit his teaching to the classroom. He also established a reputation as a clear and lucid mathematical expositor, authoring countless popular articles, book reviews, and textbooks, several published by the contemporaneous Society for the Diffusion of Useful Knowledge (S.D.U.K.) of which he was a prominent member. He wrote over 700 entries for the Society’s Penny Cyclopaedia (27 vols, 1833–1843), including one in which he introduced the term, although not the method, of ‘induction’ into mathematics [De Morgan 1838].

Figure 6. Augustus De Morgan, as sketched by his wife, around 1840.
At UCL, De Morgan’s mathematics course formed a core component of the undergraduate curriculum, which also included subjects such as Latin, Greek, and natural philosophy (i.e. physics). His students were divided into classes corresponding to the first and second years of undergraduate study, with each class being further divided into lower and higher divisions. For the lower junior class the mathematical requirements for entry were merely ‘that they shall be acquainted with Arithmetic to the extent of a knowledge of vulgar and decimal fractions’ [Anon 1827, 14]. From here, they would be introduced to further arithmetic, including the arithmetical theory of proportion, the first four books of Euclid, as well as some basic algebra up to linear equations. To provide extra material, examples and problems, De Morgan relied in part on his own textbooks, such as Elements of Arithmetic (1830) and his translation of the first three chapters of Louis Bourdon's Élémens d'Algèbre, which had been his first publication on joining UCL in 1828. Prior to the study of Euclid, De Morgan also employed material from his First Notions of Logic (1839), in keeping with his strongly held belief that, in order to foster the students' understanding of geometrical arguments, it was first necessary to introduce them to logical notions and processes.
De Morgan’s higher junior class began with Euclid Books V and VI, followed by an introduction to solid geometry, facilitated by the use of three-dimensional models. The complex theory of ratio and proportion, contained in Euclid Book V, was broached by means of the far more user-friendly approach contained in De Morgan's The Connexion of Number and Magnitude (1836), which also served as a basis for his initial treatment of trigonometry, subsequently developed more analytically in the Elements of Trigonometry and Trigonometrical Analysis (1837). After a quick review of the rules and procedures of arithmetic, students would then return to where they had left off in algebra in the lower junior course, progressing to higher order equations, logarithms and the binomial theorem. This led immediately to the study of series and the related notions of convergence and divergence, all centered on the recently formalized concept of the limit. Indeed De Morgan's Elements of Algebra (1835), used alongside this part of the course, was the first English work to contain a limit-based definition of continuity.
By the time they entered the lower division of his senior class, De Morgan’s students would have been poised to begin the study of calculus. But this was not the only topic featured. The lower senior class started with an introduction to spherical trigonometry, accompanied by a small textbook De Morgan had written for the S.D.U.K. in 1834. Projective geometry and conic sections then led into analytic geometry, which in turn motivated the study of higher algebra. According to the official college announcements, De Morgan’s senior classes were ‘confined principally to those parts of the subject which are necessary for the study of Natural Philosophy’ [Anon 1828, 42]—in other words, they were dominated by calculus-related topics. It was for this purpose that he wrote his treatise on The Differential and Integral Calculus, an 800-page compendium published in 25 installments by the S.D.U.K. between 1836 and 1842, and which De Morgan was still in the process of writing while tutoring Lovelace. Like the algebra textbook which preceded it, this book was entirely based on the concept of limits, and De Morgan used it to introduce his lower senior students to a host of differentiation and integration techniques, up to a preliminary survey of first-order linear differential equations. But the book went much further than this. In addition to its exhaustive coverage of pure calculus techniques, it also contained chapters concerning applications to algebra, geometry and mechanics; it would remain the most comprehensive English work on the subject for over a generation.
The vast majority of students at UCL proceeded no further than De Morgan's lower senior class, since that was all that was needed to pass the B.A. examination at the University of London, as well as to move on to the study of natural philosophy in the college. However, those wishing to take their studies further entered the higher senior class, in which they were exposed to ‘Subjects which all must learn who wish to become analysts, whether for Engineering or any other pursuit’ [Anon 1839, 6–7]. Here again, calculus dominated the material and De Morgan’s treatise was indispensable. Higher-order differential equations were studied at great length, particularly in relation to curves and surfaces, as well as the calculus of variations. Other subjects such as the theory of equations, three-dimensional geometry, probability theory and dynamics were also covered.
Having completed the higher senior class and been given a thorough grounding in most areas of contemporary mathematical science, De Morgan’s students would have had several options, including careers in the actuarial world, business, education and law. Although the concept of a graduate research student did not exist in Britain at this time, the higher senior class would almost certainly have served as a good starting point for those aspiring for an academic career in mathematics, since it provided guidance for those aiming for a University of London M.A. or preparing to embark on a course of higher study at Cambridge.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Lovelace's Correspondence Course with De Morgan
At this time, of course, there was no provision in Britain for the higher education of women,1 so there would never have been any question of Lovelace attending De Morgan’s lectures. But quite apart from her gender and high social status, she would have differed from De Morgan’s middle-class male students in several other respects. Since school education was not yet compulsory and the school leaving age was, on average, around fourteen, the students at UCL in De Morgan’s day were substantially younger than they are today, ranging from around 15 to 18 years of age. At 25, therefore, Lovelace would have been noticeably older than the usual college undergraduate. She would also have been far more motivated and mathematically literate than the typical UCL student at this time.
How then did the course of study undertaken by Lovelace in the early 1840s compare with the contemporaneous program offered by De Morgan at UCL? As we have seen, by the time Lovelace started studying with De Morgan, she was well acquainted with both arithmetic and elementary geometry, having essentially taught herself the early part of Euclid’s Elements, although probably no further than the end of the fourth book. She had also acquired some knowledge of algebra and trigonometry although, as seen above, her level of proficiency in these subjects is debatable. Thus, while certainly knowing more than was required for a student entering De Morgan’s lower junior class at UCL, her mathematical attainments in mid-1840 seem to place her roughly midway through the syllabus for his higher junior division. Despite this, however, her letters to De Morgan leave no doubt as to the subject in which she was most interested: calculus. And as we will see, material from this area dominates the correspondence.
The course of study that Lovelace began with De Morgan in July 1840 would nowadays be called a ‘correspondence course’. It consisted of guided independent reading along with a variety of relevant problem exercises. This material came largely from De Morgan’s own published textbooks and articles, supplemented on occasion by other relevant works, such as A Collection of Examples of the Application of the Differential and Integral Calculus (1820), written by Charles Babbage’s undergraduate contemporary and De Morgan’s erstwhile Cambridge tutor, George Peacock. The study methods fostered by De Morgan were very different to those of Lovelace’s former tutor, Dr. King, who had encouraged rote learning when reading Euclid’s Elements: ‘The words of each proposition . . . must be fixed in your mind, with their number, so that you could repeat the Book through’ [LB 172, 15 March 1834, f. 129r]. In contrast, De Morgan offered Lovelace a far more progressive and modern approach to her mathematical studies:
Festine lente,2 and above all never estimate progress by the number of pages. You can hardly be a judge of the progress you make, and I should say that it is more likely you progress rapidly upon a point that makes you think for an hour, than upon an hour’s quick reading, even when you feel satisfied [LB 170, 15 Sept. 1840, f. 14r].
As far as De Morgan was concerned, the key study skills required for success in mathematics were not speed or memorization, but thinking and understanding.
By the time the correspondence came to an end after about eighteen months, Lovelace had reached a level of familiarity, if not expertise, with much of the material covered in De Morgan’s higher junior and lower senior classes: algebra, trigonometry, complex numbers, functions, limits, infinite series, differentiation, integration, and differential equations.3 But it wasn’t all plain sailing. Let’s look now at ten sources of difficulty she encountered during her course of study with De Morgan.
Notes
1. The earliest women’s colleges in Britain were founded later in the 1840s, with De Morgan giving lessons in elementary mathematics at one of them, Bedford College, in 1849 during its first year of operation.
3. Perhaps inevitably given her concentration on calculus-related material, she could not be said to have completed a course of study entirely equivalent to those classes. Spherical trigonometry, projective geometry and conic sections are all absent from the correspondence, for example, and there is similarly no reference to subjects from the higher senior class, such as probability or the calculus of variations..
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Ten Problems Attempted by Lovelace
For the statement of each of Lovelace's ten homework exercises, click on the corresponding link in the following list. Links to the solution of each problem are included on the problem page, or can be accessed from the Solutions Page.
- Problem 1: a problem involving an algebraic manipulation that arose from a discussion of logarithmic expressions in De Morgan’s Elements of Algebra.
- Problem 2: a problem involving functional equations arising from Ada Lovelace's study of Chapter 10 of De Morgan’s Elements of Algebra.
- Problem 3: a question posed by Lovelace about imaginary numbers that was sparked by her reading of De Morgan’s article “Negative and Impossible Quantities” in the Penny Cyclopaedia.
- Problem 4: a problem involving logarithmic differentiation from Peacock’s Collection of Examples of the Application of the Differential and Integral Calculus.
- Problem 5: a problem involving the general power rule.
- Problem 6: a problem involving the Mean Value Theorem.
- Problem 7: a problem involving first-order differential equations.
- Problem 8: a problem involving integration from De Morgan’s Differential and Integral Calculus.
- Problem 9: a problem involving a complicated integral.
- Problem 10: a problem involving second-order differential equations.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 1
We begin with a very simple problem. For any student intending to study higher mathematics, the ability to manipulate and re-arrange algebraic expressions is essential. However, this is a skill that does not necessarily come easily to all students, and at first Ada Lovelace also found it difficult, as we saw in her questions to Mary Somerville. Her problems with symbolic manipulation are further evident in her correspondence with De Morgan, particularly early on in her studies. In one letter, from November 1840, she noted how difficult she found trying to verify a relatively simple point in algebra.

Figure 7. Extract from page 226 of De Morgan’s Elements of Algebra (2nd ed., 1837).
The problem arose from a discussion concerning logarithmic expressions in De Morgan’s Elements of Algebra. As can be seen from Figure 7, at the bottom of page 226 De Morgan made a simple substitution, letting
\[\frac{1+b}{1-b}=\frac{1+x}{x}\]
which he said resulted in
\[b=\frac{1}{2x+1}.\]
Lovelace had two problems with De Morgan’s claim [LB 170, 10 Nov. [1840], ff. 64r-64v]:
In the first place I do not feel satisfied that the form \(\frac{1+b}{1-b}\) is capable of being changed into the form \(\frac{1+x}{x}\). There are three suppositions we may make upon it, (supposing that it is capable of this second form). \(x\) may be less than \(b\), in which case the denominator must also be less than \(1-b\), and less in a certain given proportion, in order that the Fractional Expression may remain the same. \(x\) may \(=b\), in which case the second form can only be true on the supposition that \(1-b=x=b\), or \(b=\frac{1}{2}\). \(x\) may be greater than \(b\), in which case the denominator of the second form must also be greater than \(1-b\), in a certain given proportion, in order that the Fractional expression may remain the same.
I will leave it to the reader to determine whether her three suppositions are correct. However, it is Lovelace’s second issue that was of more concern [LB 170, 10 Nov. [1840], ff. 64v-65r]:
But secondly supposing \(\frac{1+b}{1-b}\) to be under all circumstances susceptible of the form \(\frac{1+x}{x}\), I cannot deduce from this equation \(b=\frac{1}{2x+1}\).
In other words, given the equation \[\frac{1+b}{1-b}=\frac{1+x}{x}\] Lovelace was unable to re-arrange it to solve for \(b\). This was clear evidence that there were significant gaps in her mathematical knowledge and De Morgan was quick to warn her of the periodic digressions into more elementary mathematics that would be required to fill them: ‘You understand of course that your Differential Calculus must be delayed from time to time while you make up those points of Algebra and Trigonometry which you have left behind’ [LB 170, 27 Sept. 1840, f. 16r]. And in a subsequent letter, he explained how to solve the problem. You can see his solution here.
Return to Main Problems Page.
Continue to Problem 2.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 2
Here is another algebraic problem with which Lovelace had trouble. At around the same time as the previous problem, she was struggling with the topic of functional equations, introduced in Chapter 10 of De Morgan’s Algebra. Given a particular general equation, the goal was to find the function or functions that satisfied it. On November 27, 1840, Lovelace wrote to De Morgan about the exercise in Figure 8. (Note that the functional expression \(\phi x\) means what we would write as \(\phi(x)\), or \(f(x)\), today.)
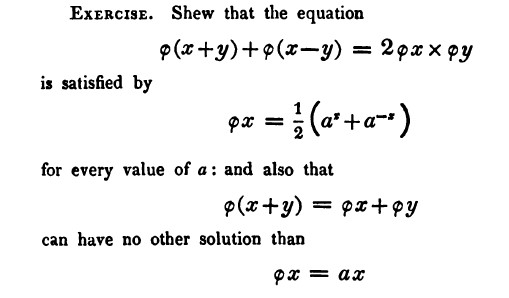
Figure 8. Exercise from p. 206 of De Morgan’s Elements of Algebra.
Lovelace was actually able to solve the second part of the problem relatively easily, since it is quite straightforward to use \(\phi(x+y)=\phi(x)+\phi(y)\) to prove that \(\phi(ax)=a\phi(x)\) and thus that \(\phi(x)\) is a linear function with \(\phi(0)=0\). But she described herself as being ‘completely baffled’ by the first part of the exercise. In a much quoted passage, she wrote:
I do not know when I have been so tantalized by anything, & should be ashamed to say how much time I have spent upon it, in vain. These Functional Equations are complete Will-o’-the-Wisps to me. The moment I fancy I have really at last got hold of something tangible & substantial, it all recedes further & further & vanishes again into thin air [LB 170, 27 Nov. [1840], ff. 149r-149v].
Starting with
\[\phi(x+y)+\phi(x-y)=2\phi(x)\phi(y)\]
she first obtained \[2\phi(x)=\frac{\phi(x+y)+\phi(x-y)}{\phi(y)}.\]
She then continued [LB 170, 27 Nov. [1840], f. 149v]:
Since \(x\) and \(y\) may have any values whatever, (at least such I conclude is of course intended), let \(y=0\). We have then
\[\begin{array}{c}2\phi(x)=\frac{\phi(x)+\phi(x)}{\phi(0)}\\
\therefore 2\phi(x)\times \phi(0)=\phi(x)+\phi(x)\\
\mbox{ or } 2\phi(x)\times \phi(0)=2\phi(x).\end{array}\]
She thus concluded (correctly) that \(\phi(0)=1\), but then claimed (incorrectly) that this was equal to \(a^0\), ‘since \(a^0\) is the only function of \(0\) which can \(= 1\)’. (The reader will of course be able to spot the flaw in her reasoning.) ‘I think so far is correct in itself,’ she wrote, ‘but whether it be the right road to the rest is another question’ [LB 170, 27 Nov. [1840], ff. 149v-150r].
Unfortunately, she did not turn out to be on the right track and after detailing a few other erroneous attempts, she gave up:
In short, many & various are the experiments I have made, but I will not detail any more. Indeed I think you may be possibly heartily sick of what I have detailed. But I wished to show you that I have not failed from want of trying, at least; & also to give you the chance of smiling at my expence [sic] [LB 170, 27 Nov. [1840], f. 151r].
Interestingly, the chief reason for Lovelace’s difficulty in this algebraic problem is completely different from that encountered in Problem 1. This time, it was not her ability to manipulate algebraic expressions that held her back, but rather a misunderstanding of what the question actually wanted her to do. Whereas the second part (which she answered correctly) wanted her to show that the functional equation led only to the result that \(\phi(x)=ax\), the first part merely required her to plug \(\phi(x)=\frac{1}{2 }(a^x+a^{-x})\) into the first equation to verify that it was satisfied.
Not long afterwards, De Morgan wrote to Lovelace to ‘put you out of your misery’ about this problem, and gave his solution in a few lines.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 3
Lovelace was no stranger to matters concerning complex and imaginary numbers. Nevertheless, the next problem showed that, despite her familiarity with them, her algebraic skills still needed improvement. While reading an article in the Penny Cyclopaedia by De Morgan on “Negative and Impossible Quantities”,4 she came across the following passage [De Morgan 1840, 134]:
It can be easily shown that any algebraical expression, however complicated, which is a function of \(\sqrt{(-1)}\) can be reduced to the form \(A+B\sqrt{(-1)}\), where \(A\) and \(B\) are possible quantities. For instance (\(k\) being \(\sqrt{(-1)}\) \[ (a+bk)^{m+nk}=e^A \cos B+k e^A \sin B \,\,\,\,\,\,\,\, [1] \]
where \(A\) and \(B\) are determined as follows. Let \[r=\sqrt{(a^2+b^2)}, \,\, \mbox{ [and] } \,\, \tan\theta=\frac{b}{a}, \,\, \mbox{[then]} \] \[A=m \log r-n\theta, B=n \log r +m\theta.\]
In a letter to De Morgan, Lovelace reported [LB 170, 9 Sept. [1841], f. 123r] that she had ‘tried a little to demonstrate this Formula’ (i.e. [1]), but was having trouble. Based on the assumption that \(\tan \theta=\frac{b}{a}\) gives \(\sin \theta=b\) and \(\cos\theta=a\), she obtained
\[\begin{array}{rcl}
(a+bk)^{m+nk}&=& (\cos \theta+k \sin\theta)^{m+nk}\\
&=&\left (e^{k\theta} \right)^{m+nk}\\
&=&e^{k(m\theta)}\times \{(e^{k(n\theta)} )\}^k \\
&=&(\cos m\theta+k \sin m\theta )\times (\cos n\theta+k \sin n\theta)^k.\end{array}\]
However, since she could get no further, she believed that the complete demonstration ‘must be a very complicated process’ [LB 170, 9 Sept. [1841], f. 123v]. In fact, she was closer than she realized but, despite a clear working knowledge of the algebra of exponents, and indeed Euler’s Formula, it was again her lack of algebraic and trigonometric experience (and consequent intuition) that ultimately prevented her from obtaining the desired result.
Can you spot Lovelace’s mistake and prove formula [1]? Click here to see the proof.
Return to Main Problems Page.
Continue to Problem 4.
Notes
4. The phrase ‘impossible quantity’ was commonly used at this time to mean an imaginary or complex number.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 4
Moving now to calculus, one of the first books De Morgan recommended that Lovelace should study was George Peacock’s Collection of Examples of the Application of the Differential and Integral Calculus, which contained a host of problems and their solutions for students to practice. One of the first problems in the book was to find the differential (not the derivative) of \(u=x^2(a+x)^3(b-x)^4\) [Peacock 1820, 2]. When attempting this question, Lovelace obtained
\[du=\{2ab-(6a-5b)x-x^2 \}x(a+x)^2(b-x)^3 dx\]
whereas the book gave
\[du=\{2ab-(6a-5b)x-9x^2 \}x(a+x)^2(b-x)^3 dx\]
`& I am inclined to think it is a misprint in the latter’ [LB 170, 10 Nov. [1840], f. 63r].

Figure 9. George Peacock (1791–1858), frontispiece of Alexander Macfarlane’s
1916 Lectures on Ten British Mathematicians of the Nineteenth Century.
So who was correct, Lovelace or Peacock?
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 5
Lovelace also tried her hand at proving standard results in calculus, such as the general power rule, namely that \[\frac{d}{dx} (x^n )=nx^{n-1}.\]
The method she used, which was correct, was to find the difference quotient \[\frac{(x+\theta)^n-x^n}{\theta},\] then use the binomial theorem to expand \((x+\theta)^n\), cancel the appropriate terms, and take the limit as \(\theta \rightarrow 0\). ‘It strikes me,’ she told De Morgan, ‘as having the advantage in simplicity, & in referring to fewer requisite previous Propositions’ [LB 170, 10 Jan. [1841], f. 82v].
Her proof was perfectly sound, but there was one small problem—its reliance on the binomial theorem. She had learnt that theorem from De Morgan’s Elements of Algebra, in which the generally accepted proof of the time was given. Unfortunately, that proof relied on a lemma which stated that: \[\lim_{w\rightarrow v}\frac{v^n-w^n}{v-w}= nv^{n-1}.\] As De Morgan was quick to point out, ‘if you take the common proof of the binomial theorem, you are reasoning in a circle, for that proof requires that it should be shown that \(\frac{v^n-w^n}{v-w}\) has the limit \(nv^{n-1}\) as \(w\) approaches \(v\). This is precisely the proposition which you have deduced from the binomial theorem’ [LB 170, [Jan. 1841], f. 34r]. A few days later, Lovelace acknowledged that ‘my proof of the limit for the function \(x^n\) is a piece of circular argument’ [LB 170, 17 Jan. [1841], f. 85v]. As she explained: ‘It had not struck me that, calling \((x+\theta)=v\), the form \(\frac{(x+\theta)^n-x^n}{\theta}\) becomes \(\frac{v^n-x^n}{v-x}\) ’ [LB 170, [Jan. 1841], f. 91r].
As an exercise, instead of using Lovelace’s method, try proving the general power rule the way De Morgan did it (for positive integer values of \(n\)). He used a result equivalent to Theorem 2 from Peacock’s Collection of Examples (see Figure 13) [De Morgan 1836-42, 51]:
If \(u\) be the product of n functions \(PQR\ldots \) then the product of all but \(P\) is \(u/P\), and so on; whence we have \[\frac{du}{dx}=\frac{u}{P}\frac{dP}{dx}+\frac{u}{Q} \frac{dQ}{dx}+\frac{u}{R} \frac{dR}{dx}+ \ldots \]
You can check your proof here.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 6
Another indispensable result in calculus is the Mean Value Theorem, which states that if a function \(f\) is continuous on a closed interval \([a,b]\) and differentiable on \((a,b)\), then there exists a value \(c\) in \((a,b)\) such that
\[\frac{f(b)-f(a)}{b-a}=f'(c).\] In his Differential and Integral Calculus, De Morgan stated it in the following form [De Morgan 1836–42, 67]:
\(\ldots\) between \(a\) and \(a+h\) \(\ldots\) it follows that \[\frac{\phi(a+h)-\phi(a)}{h}=\phi'(a+\theta h)\] is true for some positive value of \(\theta\) less than unity.
Recognizing that \(a+h=b\) and \(a+\theta h=c\in(a,b)\), since \(0<\theta<1\), it is clear that De Morgan’s statement is basically equivalent to the modern-day formulation. While Lovelace had no problem with his statement of the theorem itself, she was puzzled by his assumption that \(\theta\) was a function of \(a\) and \(h\), writing: ‘I see neither the truth of this assertion, nor do I perceive the importance of it (supposing it is true) to the rest of the argument’ [LB 170, 19 Feb. [1841], f. 100r].
De Morgan replied by asking her, rhetorically: ‘Why should \(\theta\) be independent of \(a\) and \(h\) [since] we have never proved it to be so’? [LB 170, [22 Feb. 1841], f. 42v] To demonstrate that \(\theta\) could be expressed as a function of the two values as he claimed, he let \(\psi\) be the inverse function of \(\phi'\) so that \(\psi(\phi'(x))=x\). Then, he wrote:
\[\begin{array}{l}
\frac{\phi(a+h)-\phi(a)}{h}=\phi'(a+\theta h)\\ \\
\psi \left (\frac{\phi(a+h)-\phi(a)}{h} \right )=\psi(\phi'(a+\theta h)))=a+\theta h\\ \\
\theta =\frac{ \psi \left (\frac{\phi(a+h)-\phi(a)}{h} \right ) - a}{h} \left \{\mbox{Say that this is not a function of \(a\) and \(h\), if you dare} \right .\end{array}\]
Convincing though this demonstration may seem, it turns out that Lovelace’s doubts about the validity of De Morgan’s assertion were well founded. In fact, the professor was actually incorrect: \(\theta\) is not necessarily a function of \(a\) and \(h\), and the above proof is wrong. The question is: why?
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 7
Let’s move on to questions involving integration, or at least, questions that should involve integration, such as the solution of first-order differential equations. In July 1841, De Morgan posed the following problem to Lovelace:
Try to prove the following. It is only when \(y=ax\) (\(a\) being constant) that \[\frac{dy}{dx}=\frac{y}{x}\] [LB 170, 11 July [1841], f. 112v].
In her answer, Lovelace employed a heuristic (and flawed) approach, relying on intuitive ideas about limits and derivatives (or as they were then known, ‘differential coefficients’), rather than the correct method, which required integration. But it is clear that her confidence in it was not strong: ‘I do not feel quite sure that my proof is a proof. But I think it is too’ [LB 170, 11 July [1841], f. 112v]. This was her argument:
Given as \(\frac{dy}{dx}=\frac{y}{x}\), what conditions must be fulfilled in order to make this equation possible? Firstly: I see that since \(\frac{dy}{dx}\) means a Differential Co-efficient, which from it's [sic] nature (being a Limit) is a constant & fixed thing, \(\frac{y}{x}\) must also be a constant & fixed quantity. That is \(y\) must have to \(x\) a constant Ratio which we may call \(a\). This seems to me perfectly valid. And surely a Differential Co-efficient is as fixed & invariable in it's [sic] nature as anything under the sun can be [LB 170, 15 Aug. [1841], ff. 116r-116v].
But it wasn’t long before she realized that this argument was flawed. What was the error in her reasoning? And how should this problem be solved?
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 8
Here’s another problem that involves an integral. First of all, prove for yourselves that \[\int \frac{dx}{x^2-c}=\frac{1}{2\sqrt{c}} \log\left (\frac{\sqrt{c}-x}{\sqrt{c}+x}\right )\] plus a constant, of course. De Morgan gave this result on pages 112–3 of his Differential and Integral Calculus, where he stated that it ‘becomes impossible when \(x\) is greater than \(\sqrt{c}\), for in that case the integral becomes the logarithm of a negative quantity’ [De Morgan, 1836-42, 113].
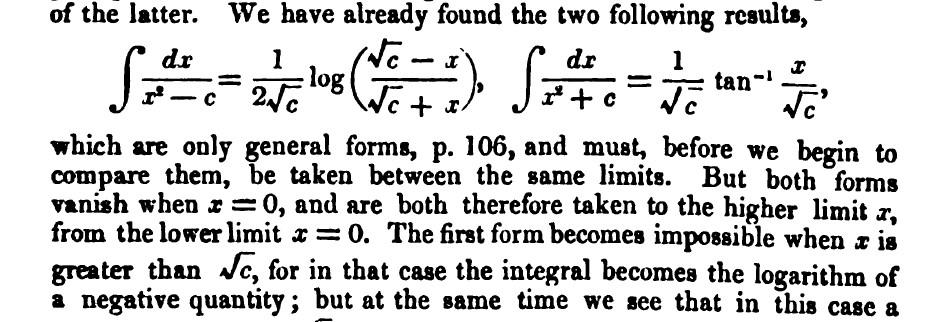
Figure 10. Part of page 113 from De Morgan’s Differential and Integral Calculus.
But Lovelace took issue with this claim. In a letter of August 1841, she observed that ‘there are surely certain cases in which negative quantities may be powers, & therefore may have Logarithms’. Thus, since, for example, \[-a^3=(-a)\times(-a)\times(-a),\] ‘\(3\) is here surely the Logarithm of a Negative Quantity. Similarly a negative quantity multiplied into itself any odd number of times will give a negative result’ [LB 170, 15 Aug. [1841], f. 116r].
Lovelace has made two mistakes here. What were they?
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 9
The integral \[\int \frac{dx}{\sqrt{A+Bx+Cx^2}}\] is more sophisticated still. Try to prove for yourself that, if \(C>0\), \[\int \frac{dx}{\sqrt{A+Bx+Cx^2}}= \frac{1}{\sqrt{C}} \log\left ( 2Cx+B+\sqrt{4C(A+Bx+Cx^2)} \right ).\] In his Calculus, letting \(A=0\), \(B=2a\), and \(C=1\), De Morgan deduced that, as he put it: \[\int \frac{dx}{\sqrt{2ax+x^2}}= \log \left( x + a + \sqrt{(2ax+x^2)} \right ) + \log 2. \mbox{ (Omit the constant.) } \]
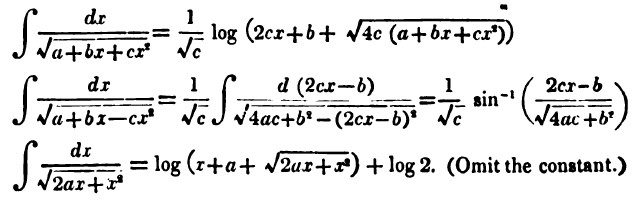
Figure 11. Part of page 116 from De Morgan’s Differential and Integral Calculus.
But when Lovelace tried to derive this result from first principles, she wrote [LB 170, 15 Aug. [1841], f. 115v]:
I cannot make it anything but \[\int \frac{dx}{\sqrt{2ax+x^2}} = \log \left ( x + 2a + \sqrt{(2ax+x^2)} \right )\] or else \[ = \log \left ( \frac{x}{2} + a + \frac{\sqrt{2ax+x^2}}{2} \right )+ \log 2 \] \(\ldots\) and I begin to suspect the book.
Her approach was straightforward. Setting \(2ax+x^2=(2a+x)x=y^2\), she derived the differential equation \((2a+x)dx=ydy\), from which she formed the integral \[\int \frac{dx}{y}=\int \frac{dy}{2a+x} .\]
Then, by analogy with the ‘fact’ that \(\frac{dx+dy}{x+y}=\frac{dx}{y}\), she obtained \[ \begin{array}{lcl} \int \frac{dx}{y} &=& \int \frac{d(2a+x)+dy}{(2a+x)+y}\\ &=&\int \frac{d(2a+x+y)}{2a+x+y}\\ &=&\log(2a+x+y)\\ &=&\log(2a+x+\sqrt{2ax+x^2})\\ &=& \log\left ( \frac{x}{2} + a + \frac{\sqrt{2ax+x^2}}{2}\right )+\log 2.\end{array}\]
In addition to her erroneous assumption that \[\frac{dx+dy}{x+y}=\frac{dx}{y}\]
De Morgan was able to spot that, given \(y^2=(2a+x)x\), she had forgotten to apply the product rule, so that her differential equation should have been \[ydy=\frac{1}{2} xdx + \frac{1}{2} (2a+x)dx \] or \[ydy=(x+a)dx.\,\,\,\,\, \mbox{[2]}\] After correcting these errors, Lovelace wrote in a subsequent letter [LB 170, 21 Aug. [1841], f. 121v], that
we arrive then in my corrected paper, at \[\begin{array}{rcl}\int \frac{dx}{\sqrt{2ax+x^2}} &=& \log \left( x + a + \sqrt{(2ax+x^2)} \right )\\ &=&\log\left( \frac{x}{2} + \frac{a}{2} + \frac{\sqrt{2ax+x^2}}{2} \right )+\log 2.\end{array}\]
Can you derive Lovelace’s final result from equation [2]?
In his acknowledgement, De Morgan observed that Lovelace’s answer agreed with his result in all respects ‘but the log 2, which being a Constant, matters nothing’ [LB 170, 21 Aug. [1841], f. 121v]. Explain why his and Lovelace’s results are equivalent.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 10
Our final problem comes close to the end of Lovelace’s correspondence course with De Morgan. By early November 1841, she had progressed to the subject of second-order differential equations. One of the examples with which she had trouble was on page 156 of De Morgan’s Calculus. Given the nonhomogeneous equation
\[\frac{d^2 u}{d\theta^2 }+u=\cos\theta\]
De Morgan gave its general solution as
\[u=C \sin \theta + C' \cos \theta + \sin\theta \int cos^2 \theta d \theta - \frac{1}{2} \cos \theta \int \sin 2\theta d\theta,\] which, since
\[ \int \cos^2 \theta d\theta = \frac{1}{2} \theta + \frac{1}{4} \sin 2 \theta \, \, \mbox{ and } \,\, \int \sin 2\theta d\theta = -\frac{1}{2} \cos 2\theta \] resulted in
\[u=C \sin\theta + C' \cos \theta +\frac{1}{2}\theta \sin \theta + \frac{1}{4} \sin 2 \theta \sin \theta+ \frac{1}{4} \cos\theta \cos 2\theta.\] Using double angle formulae, he converted this into
\[u=C \sin \theta + C' \cos \theta + \frac{1}{2}\theta \sin \theta+ \frac{1}{4} \cos \theta,\] which he then expressed in its final form as
\[u=C \sin \theta+C' \cos \theta + \frac{1}{2} \sin \theta,\] along with a challenge: ‘Explain this step?’ (See Figure 12).
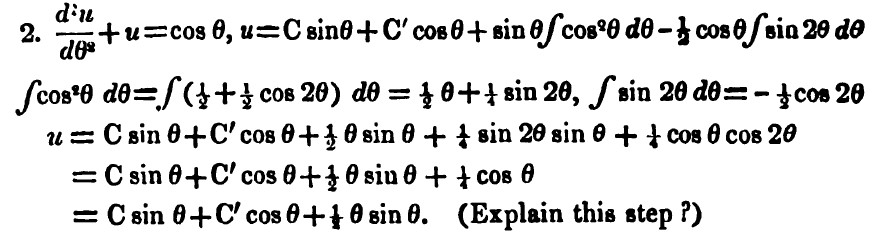
Figure 12. Problem from page 156 of De Morgan’s Differential and Integral Calculus.
The trouble was, as Lovelace remarked in a letter to De Morgan, ‘I cannot “explain this step”.’ She noted that ‘in the previous line, we have: \[\begin{array}{r} (1) \ldots u = C \sin \theta +C' \cos \theta + \frac{1}{2}\theta \sin \theta + \frac{1}{4} \cos \theta \mbox{ (quite clear)} \end{array}\] \[\begin{array}{rcl} (2) \ldots \mbox{ And } u &=&\cos \theta -\frac{d^2 u}{d \theta ^2 } \mbox{ (by hypothesis)} \\ &=& \frac{1}{4} \cos \theta+\left (\frac{3}{4} \cos \theta-\frac{d^2 u}{d\theta^2} \right ) \end{array}\]
whence one may conclude that \[C \sin\theta+C' \cos \theta + \frac{1}{2}\theta\sin \theta=\frac{3}{4}\cos \theta-\frac{d^2 u}{d\theta^2} \] But how \(u=C \sin \theta+C' \cos \theta+\sin\theta\cdot\frac{1}{2} \theta\) is to be deduced I do not discover.’ [LB 170, 4 Nov. [1841], ff. 132v-133r]
Not deterred, she tried again:
By subtracting \(\frac{1}{4}\cos \theta\) from both sides of (1), we get \[u-\frac{1}{4} \cos \theta= C \sin \theta+C' \cos \theta+ \frac{1}{2} \theta \sin \theta\] But unless \(\frac{1}{4} \cos \theta=0\), (which would only be the case I conceive if \(\theta=\pi/2\)), I do not see how to derive the equation \(\ldots\) [LB 170, 4 Nov. [1841], f. 133r].
De Morgan’s final solution is certainly correct. So can you explain why the \(\frac{1}{4} \cos \theta\) mysteriously disappears?
Return to Main Problems Page.
Continue to Main Solutions Page.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solutions
To see how to solve the problems described in this article, click on the "Solution" links in the following list. For a reminder of the problem statement, you can click on the corresponding "Problem" link.
- Solution to a Rule of Three Problem that puzzled 10-year old Lovelace.
- Solution given by Somerville to a Trigonometry Problem that perplexed a young Lovelace.
- Solution given by De Morgan to Problem 1, a problem involving algebraic manipulation that arose from a discussion of logarithmic expressions in De Morgan’s Elements of Algebra.
- Solution given by De Morgan to Problem 2, a problem involving functional equations arising from Ada Lovelace's study of Chapter 10 of De Morgan’s Elements of Algebra.
- Solution given by De Morgan to Problem 3, a question posed by Lovelace about imaginary numbers that was sparked by her reading of De Morgan’s article “Negative and Impossible Quantities” in the Penny Cyclopaedia.
- Solution to Problem 4, a problem involving logarithmic differentiation from Peacock’s Collection of Examples of the Application of the Differential and Integral Calculus, based on theorems given by Peacock.
- Solution based on De Morgan’s approach to Problem 5, a problem involving the general power rule.
- Why the Solution given by De Morgan to Problem 6, a problem involving the Mean Value Theorem, was problematic.
- Why the Solution given by Lovelace to Problem 7, a problem involving first-order differential equations, was flawed.
- Errors in the Solution given by Lovelace to Problem 8, a problem involving integration from De Morgan’s Differential and Integral Calculus.
- Why the Solution given by Lovelace to Problem 9, a problem involving a complicated integral, is equivalent to the solution given by De Morgan.
- Explanation of the Solution given by Lovelace to Problem 10, a problem involving second-order differential equations.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solution to Rule of Three Problem
In this Rule of Three problem, \(a=750\), \(b=22,500\), and \(c=1200\). Therefore,
\[x=\frac{22,500 \times 1200}{750}=36,000.\]
Return to Main Solutions Page.
Continue to Somerville's solution of the trigonometry problem.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Mary Somerville’s Solution to the Trigonometry Problem
Somerville’s solution to the slightly harder Trigonometry Problem posed by Lovelace is contained in a letter, written on November 28, 1835 [LB 174, 28 Nov. 1835, ff. 31v-32r]. In it, Somerville writes:
The formulae proposed are
\[\begin{array}{c}R \sin a=\sin(a-b) \cos b + \cos(a-b) \sin b\\
R \cos a=\cos(a-b) \cos b - \sin(a-b) \sin b\end{array}\]
If the first be multiplied by \(\cos b\), and the other by \(\sin b\), their difference is
\[R (\sin a \cos b - \cos a \sin b )= \sin(a-b) ( \cos^2 b + \sin^2 b)\]
but \(\cos^2 b+\sin^2 b=R^2\), hence after dividing by \(R\)
\[\sin a \cos b - \cos a \sin b = R \sin(a-b).\]
Again, if the first be multiplied by \(\sin b\) and the second by \(\cos b\), their sum is
\[R(\sin a \sin b +\cos a \cos b ) = \cos(a-b) ( \sin^2 b + \cos^2 b).\]
Substituting \(R^2\) for \(\sin^2 b+\cos^2 b\), and then dividing by \(R\) you will find
\[\sin a \sin b + \cos a \cos b = R \cos(a-b).\]
Return to Main Solutions Page.
Continue to Solution to Problem 1.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solution to Problem 1
De Morgan enclosed his solution to Problem 1 in a letter to Lovelace of November 14, 1840 [LB 170, 14 Nov. 1840, f. 20v]. Beginning with the initial equation
\[\frac{1+b}{1-b}=\frac{1+x}{x}\]
he multiplied both sides by \(1-b\) and \(x\):
\[(1+b)x=(1-b)(1+x).\]Then, distributing
\[x+bx=1+x-b-bx\]cancelling an \(x\) from both sides
\[bx=1-b-bx\]collecting like terms
\[2bx+b=1\]factoring out the \(b\)
\[(2x+1)b=1\]and finally dividing by \(2x+1\) gave
\[b=\frac{1}{2x+1}.\]
Return to Main Solutions Page.
Continue to Solution to Problem 2.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solution to Problem 2
Here is a transcription of the letter containing De Morgan’s solution to Problem 2, which he included in a letter [LB 170, [Nov. 1840], ff. 27r-27v]:
My dear Lady Lovelace,
I can soon put you out of your misery about p. 206. You have shown correctly that \(\phi(x+y)=\phi(x)+\phi(y)\) can have no other solution than \(\phi(x)=ax\), but the preceding question is not of the same kind; it is not show that there can be no other solution except \(\frac{1}{2} (a^x+a^{-x})\) but show that \(\frac{1}{2} (a^x+a^{-x})\) is a solution: that is, try this solution.
\[\begin{array}{rcl}\phi(x+y)&=&\frac{1}{2} (a^{x+y}+a^{-x-y} )\\
\phi(x-y)&=&\frac{1}{2} (a^{x-y}+a^{-x+y} )\\
\phi(x+y)+\phi(x-y)&=&\frac{1}{2} (a^{x+y}+a^{-x-y}+a^{x-y}+a^{-x+y} )\end{array}\]
\[\begin{array}{ll}\mbox{[On the other hand]}\hspace{20pt}& 2\phi(x)\cdot \phi(y)=2\cdot \frac{1}{2} (a^x+a^{-x} )\cdot \frac{1}{2} (a^y+a^{-y} )\\
& =\frac{1}{2} (a^x+a^{-x} )(a^y+a^{-y} )\\
& =\frac{1}{2} (a^{x+y}+a^{-x-y}+a^{x-y}+a^{-x+y} )\end{array}\]
the same as before.
To prove that this can be the only solution would be above you.
I think you have got all you were meant to get from the chapter on functions. The functional equations which can be fully solved are few in number.
Yours very truly
A De Morgan
Return to Main Solutions Page.
Continue to Solution to Problem 3.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solution to Problem 3
Since \(\tan \theta=b/a\), Lovelace assumed that \(\sin\theta=b\) and \(\cos\theta=a\) in her attempt to solve Problem 3. However, \(\sin\theta\) and \(\cos\theta\) are actually equal to \(b/r\) and \(a/r\), respectively; so the expression Lovelace derived should have been
\[\begin{array}{lcl} (a+bk)^{m+nk}&=& r^{m+nk} (\cos\theta+k \sin\theta)^{m+nk}\\
&=&r^{m+nk} (e^{k\theta})^{m+nk}\\
&=&r^{m+nk}\cdot e^{k(m\theta)} \cdot e^{-n\theta}\\
&=&r^m\cdot e^{-n\theta} \cdot r^{nk} \cdot e^{k(m\theta)}\\
&=&e^{m \log r-n\theta}\cdot e^{k(n \log r+m\theta)}\\
&=&e^A (\cos B + k \sin B ).\end{array}\]
Return to Main Solutions Page.
Continue to Solution to Problem 4.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solution to Problem 4
Unfortunately, Lovelace’s work for Problem 4 no longer exists, but she probably attempted to solve it by a repeated application of the product rule. While there is nothing inherently wrong with this approach, it is clear that Peacock intended the problem to be solved using one of three theorems he stated in a footnote on the same page (see Figure 13). These theorems are simply three cases of what we nowadays call logarithmic differentiation, which can indeed simplify the process of differentiating products of multiple functions. But Lovelace was none the wiser, being completely mystified by the content of Peacock’s note: ‘Not one of the three theorems it contains is intelligible to me,’ she wrote [LB 170, 10 Nov. [1840], f. 63v].

Figure 13. Footnote on page 2 of George Peacock’s Collection of Examples of the Application of the Differential and Integral Calculus (1820).
If she had understood the meaning of these theorems, she could have applied theorem (2) to \(u=x^2 (a+x)^3 (b-x)^4\), where \(v_1=x^2\), \(v_2= (a+x)^3\), and \(v_3= (b-x)^4\). This would have given her
\[\begin{array}{ccl}du&=&x^2 (a+x)^3 (b-x)^4 \left \{\frac{2x}{x^2} + 3\frac{(a+x)^2}{(a+x)^3} - \frac{4(b-x)^3}{ (b-x)^4} \right \}dx \\
&=&x^2 (a+x)^3 (b-x)^4 \left \{\frac{2}{x}+\frac{3}{a+x}-\frac{4}{b-x}\right \}dx\\
&=&x^2 (a+x)^3 (b-x)^4 \left \{\frac{(2(a+x)(b-x)+3x(b-x)-4x(a+x)}{ x(a+x)(b-x)}\right \}dx\\
&=&x^2 (a+x)^3 (b-x)^4 \left \{\frac{2ab-6ax+5bx- 9x^2}{x(a+x)(b-x)}\right \}dx\\
&=&x (a+x)^2 (b-x)^3 (2ab-(6a-5b)x-9x^2 )dx.\end{array}\]
Thus Peacock’s answer was in fact correct.
Lovelace’s mistake was that she did not apply the chain rule to \((b-x)^4\) correctly, and obtained \(4 (b-x)^3 \)instead of \(-4 (b-x)^3\). As De Morgan explained to her: ‘It is very common to suppose that if \(\phi(x)\) differentiated gives \(\psi(x)\), then \(\phi(-x)\) gives \(\psi(-x)\), but this should be \(\psi(-x)\times \mbox{diff. co.}(-x)\) or \(\psi(-x)\times -1\)’ [LB 170, 14 Nov. 1840, f. 20r]. Sure enough, once Lovelace rectified her mistake she obtained the correct answer.
Return to Main Solutions Page.
Continue to Solution to Problem 5.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solution to Problem 5
To set up De Morgan's approach to solving Problem 5, let \(u\) be the product of \(n\) functions, \(f_1(x),f_2(x), \ldots ,f_n(x)\), where \(f_1(x)=f_2(x)=\ldots = f_n(x)=x\). In other words, let \(u=x^n\). Then using De Morgan’s version of Peacock’s Theorem 2:
\[\Large{ \begin{array}{lcl} \frac{du}{dx} &=& \frac{u}{f_1(x)}\cdot \frac{df_1}{dx} + \frac{u}{f_2(x)}\cdot\frac{df_2}{dx} + \frac{u}{f_3(x)}\cdot\frac{df_3}{dx} + \ldots + \frac{u}{f_n(x)}\cdot\frac{df_n}{dx} \\ \\ &=& \frac{x^n}{x }\cdot \frac{dx}{dx} + \frac{x^n}{x} \cdot \frac{dx}{dx} + \frac{x^n}{x} \cdot \frac{dx}{dx} + \ldots + \frac{x^n}{x} \cdot \frac{dx}{dx}\\ \\ &=& x^{n-1}+x^{n-1}+x^{n-1}+\ldots+x^{n-1} \,\,\,\, (n \mbox{ times}) \\ \\ &=&nx^{n-1}. \end{array} }\]
Return to Main Solutions Page.
Continue to Solution to Problem 6.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solution to Problem 6
In attempting to prove in Problem 6 that
\[\Large{\theta=\frac{\psi\left(\frac{\phi(a+h)-\phi(a)}{h}\right)-a}{h}}\]
De Morgan made the assumption that the function \(\phi'\) is always invertible in the domain under consideration. And as any good calculus student will know, this is by no means necessarily true.
Return to Main Solutions Page.
Continue to Solution to Problem 7.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solution to Problem 7
In trying to solve the differential equation in Problem 7, \[\frac{dy}{dx}=\frac{y}{x},\] Lovelace’s reasoning was that, since the derivative \(dy/dx\) is a limit, and since a limit is a ‘constant \& fixed thing’, this must imply that the ratio \(y/x\) is also a constant. Calling this constant \(a\) would mean that \[\frac{y}{x}=a\] or \[y=ax.\]
But of course the flaw in this argument is that limits of functions are not in general equal to constants. Indeed, taking the standard definition of the derivative as \[f'(x) = \lim_{h \rightarrow 0}\frac{f(x+h)-f(x)}{h}\] we can see that, while the quantity \(h\) approaches zero, the variable \(x\) is free to assume any value whatsoever—quite the opposite of a constant.
The simplest method for solving the equation correctly would be to separate the variables and integrate, giving \[\int \frac{dy}{y} =\int \frac {dx}{x}\] or \[ \log y = \log x+c,\] which, letting \(a=e^c\), is \[y=ax.\]
Return to Main Solutions Page.
Continue to Solution to Problem 8.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solution to Problem 8
In the 19th century, the word ‘impossible’ was widely used in the way that ‘imaginary’ is employed by mathematicians today, with real numbers often referred to as ‘possible’. Thus, in claiming in connection to Problem 8 that the expression
\[\int \frac{dx}{x^2-c} = \frac{1}{2\sqrt{c}} \log\left(\frac{\sqrt{c}-x}{\sqrt{c}+x}\right )\] ‘becomes impossible when \(x\) is greater than \(\sqrt{c}\),’ De Morgan merely meant that when the integrand is positive, the logarithm on the right will become a logarithm of a negative number, and hence imaginary, or more accurately, complex. Lovelace’s first mistake was therefore to have misinterpreted the term ‘impossible quantity’ to mean something meaningless or illogical. As she said:
I fancy I had a little misunderstood the mathematical meaning of the words impossible quantity. I have loosely interpreted it as being equivalent to ‘an absurdity’ [LB 170, 21 Aug. [1841], f. 122r].
Her second mistake was to have assumed in the standard definition of a logarithm with base \(a\), that \(a\) could be positive or negative. Thus, if a logarithm happened to be odd, she inferred that its base could be negative, a circumstance which, she speculated, ‘would I think be admitted theoretically (tho' inconvenient practically) on the common beginner's introduction on the Theory of Logarithms. Am I right?’ [LB 170, 21 Aug. [1841], f. 122r]. A cursory glance at page 224 of De Morgan’s Elements of Algebra—which, as the letters attest, she had certainly read—reveals that the answer to this question is no!
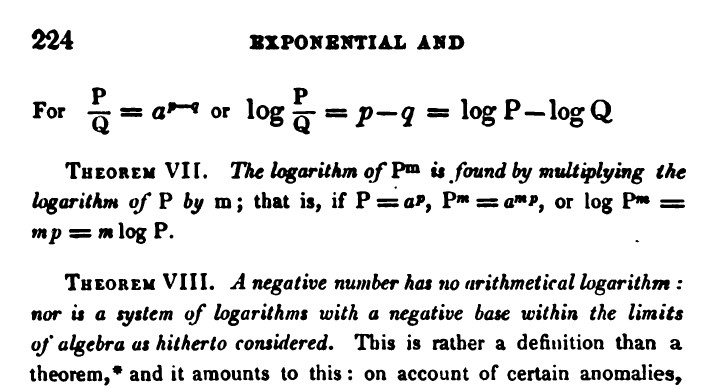
Figure 14. Theorem VIII on page 224 of De Morgan’s Elements of Algebra
states that logarithms cannot have a negative base.
Return to Main Solutions Page.
Continue to Solution to Problem 9.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solution to Problem 9
Since \(y^2=2ax+x^2=(2a+x)x\) in Lovelace's approach to Problem 9, using the product rule we have \[ydy=(x+a)dx \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, [2]\] so that \[(x+a)dy+ydy=(x+a)(dx+dy)\] or \[(x+a+y)dy=(x+a)(dx+da+dy)\] and thus \[\frac{dy}{x+a} = \frac{d(x+a+y)}{x+a+y}.\] Now since, by [2], \[\frac{dy}{x+a}=\frac{dx}{y}\] this means that \[\frac{dx}{y}=\frac{d(x+a+y)}{x+a+y}.\] So, recalling that \(y^2=2ax+x^2\), we have \[\int \frac{dx}{\sqrt{2ax+x^2}} = \log(x+a+\sqrt{2ax+x^2}) = \log\left (\frac {x}{2} +\frac{a}{2} + \frac{\sqrt{2ax+x^2}}{2} \right )+ \log 2\] which is Lovelace’s result.
Now recall that De Morgan had obtained \[\int \frac{dx}{\sqrt{2ax+x^2}} = \log(x+a+\sqrt{2ax+x^2}) + \log 2.\] Strictly speaking, his result should read \[\int \frac{dx}{\sqrt{2ax+x^2}} = \log(2x+2a+2\sqrt{2ax+x^2}) +C\] and Lovelace’s result should be \[\int \frac{dx}{\sqrt{2ax+x^2}} = \log(x + a +\sqrt{2ax+x^2}) +C'.\] Thus, letting Lovelace’s constant of integration \(C'=C+\log 2\) reveals that the two results are equivalent and also explains De Morgan’s remark that the \(\log 2\), ‘being a Constant, matters nothing.’
Return to Main Solutions Page.
Continue to Solution to Problem 10.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Solution to Problem 10
To reconcile the solutions to Problem 10 given by Lovelace and De Morgan, how can the solution \[u=C \sin\theta+C' \cos\theta+\frac{1}{2} \theta \sin \theta+ \frac{1}{4} \cos\theta\] be converted into its final form \[u=C \sin\theta+C' \cos\theta+\frac{1}{2} \theta \sin\theta ?\] As Lovelace suggested, substituting \(\theta=\frac{\pi}{2}\) would obviously eliminate the \(\frac{1}{4} \cos\theta\) term, but that clearly would not be correct as the other terms would also be changed. Why then does the \(\frac{1}{4} \cos\theta\) disappear?
The answer lies in the fact that the two \(\cos\theta\) terms both have constant coefficients, namely, \(C'\) and \(\frac{1}{4}\). They can thus be combined into a single term \[\left(C'+\frac{1}{4}\right) \cos\theta\] or \[C'' \cos\theta\] where \(C''=C'+\frac{1}{4}\). Thus De Morgan’s final answer, while not wrong, is slightly misleading, since in light of the above discussion it would be better expressed as \[u=C \sin\theta+C'' \cos\theta+ \frac{1}{2} \theta \sin\theta.\]
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Conclusion and References
Conclusion
The mathematical content of Ada Lovelace’s correspondence with Augustus De Morgan reveals a great deal to the modern reader. It shows that in a period of just eighteen months, her mathematical proficiency grew dramatically, as evidenced by the noticeable increase in the sophistication of her questions: from re-arranging simple algebraic expressions to the solution of second-order differential equations. But from a modern-day perspective, perhaps the most striking feature is the similarity between the deficiencies Lovelace displayed in her studies with De Morgan and the shortcomings exhibited by present-day students of mathematics. These include a lack of fluency in algebra, the misunderstanding of terminology and concepts, circular reasoning, and errors in applying rules or interpreting questions. The ten problems we have highlighted could all be given to today’s calculus students, not just as valuable exercises in mathematics, but as examples of pitfalls to avoid. Indeed, for both student and teacher, spotting Lovelace’s errors is arguably as instructive as solving the problems themselves. Fundamentally, they all illustrate the value of practice, the necessity of asking questions, and the essential role of a good teacher. In this respect, the difficulties faced by Ada Lovelace when learning calculus 180 years ago—and the remedies for them—differ very little from those facing our students today.
References
Archival Sources
Lovelace Byron Papers (Bodleian Library, Oxford), Boxes 41, 118, 170, 172, 174, 175. Reproductions and transcripts of Box 170 (the correspondence with De Morgan) may be viewed on the website of the Clay Mathematics Institute. In the citations, ‘Lovelace Byron Papers, Box n’ is abbreviated as ‘LB n’.
Somerville Papers, (Bodleian Library, Oxford), Dep. c.367.
Published Sources
Anon. 1827. Statement by the Council of the University of London, Explanatory of the Nature and Objects of the Institution. London: Richard Taylor.
Anon. 1828. Second Statement by the Council of the University of London, Explanatory of the Plan of the Institution. London: Richard Taylor.
Anon. 1839. University College, London. Session 1839–40. Faculty of Arts and Laws. London: Richard & John E. Taylor.
Babbage, C. 1864. Passages from the Life of a Philosopher. London: Longman, Green, Longman, Roberts, & Green.
De Morgan, A. 1836–42. The Differential and Integral Calculus. London: Baldwin and Cradock.
De Morgan, A. 1837. Elements of Algebra, Preliminary to the Differential Calculus. 2nd edition. London: Taylor and Walton.
De Morgan, A. 1838. Induction (Mathematics). In The Penny Cyclopædia of the Society for the Diffusion of Useful Knowledge, vol. 12, 465–466. London: Charles Knight and Co.
De Morgan, A. 1840. Negative and Impossible Quantities. In The Penny Cyclopædia of the Society for the Diffusion of Useful Knowledge, vol. 16, 130–138. London: Charles Knight and Co.
Hollings, C., Martin, U., and Rice, A. 2017a. The early mathematical education of Ada Lovelace, BSHM Bulletin: Journal of the British Society for the History of Mathematics 32, 221–234.
Hollings, C., Martin, U., and Rice, A. 2017b. The Lovelace–De Morgan mathematical correspondence: A critical re-appraisal, Historia Mathematica 44, 202–231.
Hollings, C., Martin, U., and Rice, A. 2018. Ada Lovelace: The Making of a Computer Scientist. Oxford: Bodleian Library.
Lovelace, A. A. 1843. Sketch of the Analytical Engine invented by Charles Babbage Esq. By L. F. Menabrea, of Turin, officer of the Military Engineers, with notes upon the memoir by the translator. Taylor’s Scientific Memoirs 3, 666–731.
Peacock, G. 1820. A Collection of Examples of the Applications of the Differential and Integral Calculus. Cambridge: J. Deighton and Sons.
Rice, A. 1996. Augustus De Morgan: Historian of Science. History of Science 34, 201–240.
Rice, A. 1997. Inspiration or desperation? Augustus De Morgan’s appointment to the Chair of Mathematics at London University in 1828. British Journal for the History of Science 30, 257–274.
Rice, A. 1999. What Makes a Great Mathematics Teacher? The Case of Augustus De Morgan. The American Mathematical Monthly 106 (6), 534–552.
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Acknowledgements, Image Credits and About the Author
Acknowledgements
My thanks are due to Christopher Hollings and Ursula Martin, without whom my knowledge of Ada Lovelace’s mathematics would be very small. Transcriptions of Lovelace’s correspondence with De Morgan were made by Christopher Hollings in 2015 and may be viewed online (along with high-quality images of the original letters) at: https://www.claymath.org/content/correspondence-de-morgan-0.
Image Credits
All images used in this paper are in the public domain.
About the Author
Adrian Rice is the Dorothy and Muscoe Garnett Professor of Mathematics at Randolph-Macon College in Ashland, Virginia, USA. His research focuses on the history of mathematics, specifically the development of algebra, analysis and logic in 19th- and early 20th-century Britain. He has received several awards for outstanding expository writing, most recently in 2021, when he was awarded the Catherine Richards Prize by the Institute of Mathematics and its Applications for his 2020 article "Srinivasa Ramanujan (1887–1920): The Centenary of a Remarkable Mathematician."