Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 2
Here is another algebraic problem with which Lovelace had trouble. At around the same time as the previous problem, she was struggling with the topic of functional equations, introduced in Chapter 10 of De Morgan’s Algebra. Given a particular general equation, the goal was to find the function or functions that satisfied it. On November 27, 1840, Lovelace wrote to De Morgan about the exercise in Figure 8. (Note that the functional expression \(\phi x\) means what we would write as \(\phi(x)\), or \(f(x)\), today.)
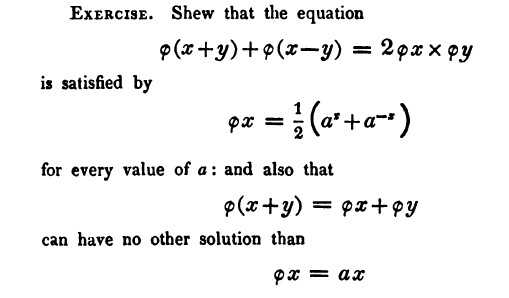
Figure 8. Exercise from p. 206 of De Morgan’s Elements of Algebra.
Lovelace was actually able to solve the second part of the problem relatively easily, since it is quite straightforward to use \(\phi(x+y)=\phi(x)+\phi(y)\) to prove that \(\phi(ax)=a\phi(x)\) and thus that \(\phi(x)\) is a linear function with \(\phi(0)=0\). But she described herself as being ‘completely baffled’ by the first part of the exercise. In a much quoted passage, she wrote:
I do not know when I have been so tantalized by anything, & should be ashamed to say how much time I have spent upon it, in vain. These Functional Equations are complete Will-o’-the-Wisps to me. The moment I fancy I have really at last got hold of something tangible & substantial, it all recedes further & further & vanishes again into thin air [LB 170, 27 Nov. [1840], ff. 149r-149v].
Starting with
\[\phi(x+y)+\phi(x-y)=2\phi(x)\phi(y)\]
she first obtained \[2\phi(x)=\frac{\phi(x+y)+\phi(x-y)}{\phi(y)}.\]
She then continued [LB 170, 27 Nov. [1840], f. 149v]:
Since \(x\) and \(y\) may have any values whatever, (at least such I conclude is of course intended), let \(y=0\). We have then
\[\begin{array}{c}2\phi(x)=\frac{\phi(x)+\phi(x)}{\phi(0)}\\
\therefore 2\phi(x)\times \phi(0)=\phi(x)+\phi(x)\\
\mbox{ or } 2\phi(x)\times \phi(0)=2\phi(x).\end{array}\]
She thus concluded (correctly) that \(\phi(0)=1\), but then claimed (incorrectly) that this was equal to \(a^0\), ‘since \(a^0\) is the only function of \(0\) which can \(= 1\)’. (The reader will of course be able to spot the flaw in her reasoning.) ‘I think so far is correct in itself,’ she wrote, ‘but whether it be the right road to the rest is another question’ [LB 170, 27 Nov. [1840], ff. 149v-150r].
Unfortunately, she did not turn out to be on the right track and after detailing a few other erroneous attempts, she gave up:
In short, many & various are the experiments I have made, but I will not detail any more. Indeed I think you may be possibly heartily sick of what I have detailed. But I wished to show you that I have not failed from want of trying, at least; & also to give you the chance of smiling at my expence [sic] [LB 170, 27 Nov. [1840], f. 151r].
Interestingly, the chief reason for Lovelace’s difficulty in this algebraic problem is completely different from that encountered in Problem 1. This time, it was not her ability to manipulate algebraic expressions that held her back, but rather a misunderstanding of what the question actually wanted her to do. Whereas the second part (which she answered correctly) wanted her to show that the functional equation led only to the result that \(\phi(x)=ax\), the first part merely required her to plug \(\phi(x)=\frac{1}{2 }(a^x+a^{-x})\) into the first equation to verify that it was satisfied.
Not long afterwards, De Morgan wrote to Lovelace to ‘put you out of your misery’ about this problem, and gave his solution in a few lines.