Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 8
Here’s another problem that involves an integral. First of all, prove for yourselves that \[\int \frac{dx}{x^2-c}=\frac{1}{2\sqrt{c}} \log\left (\frac{\sqrt{c}-x}{\sqrt{c}+x}\right )\] plus a constant, of course. De Morgan gave this result on pages 112–3 of his Differential and Integral Calculus, where he stated that it ‘becomes impossible when \(x\) is greater than \(\sqrt{c}\), for in that case the integral becomes the logarithm of a negative quantity’ [De Morgan, 1836-42, 113].
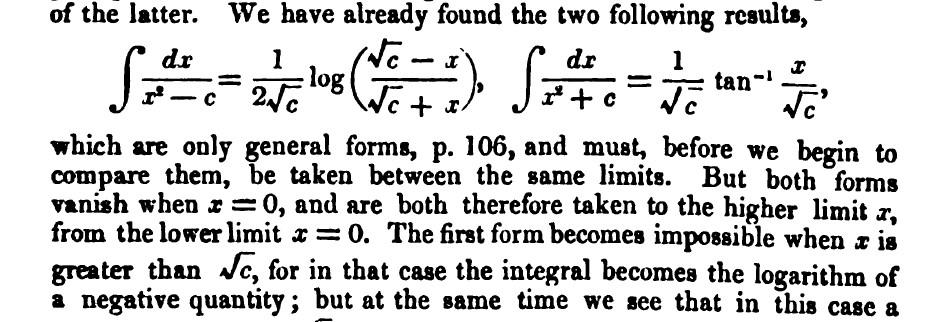
Figure 10. Part of page 113 from De Morgan’s Differential and Integral Calculus.
But Lovelace took issue with this claim. In a letter of August 1841, she observed that ‘there are surely certain cases in which negative quantities may be powers, & therefore may have Logarithms’. Thus, since, for example, \[-a^3=(-a)\times(-a)\times(-a),\] ‘\(3\) is here surely the Logarithm of a Negative Quantity. Similarly a negative quantity multiplied into itself any odd number of times will give a negative result’ [LB 170, 15 Aug. [1841], f. 116r].
Lovelace has made two mistakes here. What were they?