In this Rule of Three problem, \(a=750\), \(b=22,500\), and \(c=1200\). Therefore,
\[x=\frac{22,500 \times 1200}{750}=36,000.\]

Return to Main Solutions Page.
Continue to Somerville's solution of the trigonometry problem.

Somerville’s solution to the slightly harder Trigonometry Problem posed by Lovelace is contained in a letter, written on November 28, 1835 [LB 174, 28 Nov. 1835, ff. 31v-32r]. In it, Somerville writes:

The formulae proposed are
\[\begin{array}{c}R \sin a=\sin⁡(a-b)  \cos ⁡b +  \cos⁡(a-b)  \sin b\\
R \cos a=\cos⁡(a-b)  \cos ⁡b -  \sin⁡(a-b)  \sin b\end{array}\]

If the first be multiplied by \(\cos ⁡b\), and the other by \(\sin ⁡b\), their difference is

\[R (\sin a \cos b - \cos a \sin b )= \sin⁡(a-b) ( \cos^2 ⁡b +  \sin^2 b)\]

but \(\cos^2 b+\sin^2 b=R^2\), hence after dividing by \(R\)
\[\sin ⁡a  \cos ⁡ b - \cos ⁡a \sin ⁡b = R \sin⁡(a-b).\]

Again, if the first be multiplied by \(\sin ⁡b\) and the second by \(\cos ⁡b\), their sum is

\[R(\sin ⁡a  \sin ⁡ b +\cos ⁡a \cos ⁡b ) = \cos⁡(a-b)  ( \sin^2 ⁡b +  \cos^2 b).\]

Substituting \(R^2\) for \(\sin^2 b+\cos^2 b\), and then dividing by \(R\) you will find
\[\sin ⁡a  \sin ⁡ b + \cos ⁡a \cos b = R \cos⁡(a-b).\]

Return to Main Solutions Page.
Continue to Solution to Problem 1.

De Morgan enclosed his solution to Problem 1 in a letter to Lovelace of November 14, 1840 [LB 170, 14 Nov. 1840, f. 20v]. Beginning with the initial equation
\[\frac{1+b}{1-b}=\frac{1+x}{x}\]
he multiplied both sides by \(1-b\) and \(x\):
\[(1+b)x=(1-b)(1+x).\]Then, distributing
\[x+bx=1+x-b-bx\]cancelling an \(x\) from both sides
\[bx=1-b-bx\]collecting like terms
\[2bx+b=1\]factoring out the \(b\)
\[(2x+1)b=1\]and finally dividing by \(2x+1\) gave
\[b=\frac{1}{2x+1}.\]

Return to Main Solutions Page.
Continue to Solution to Problem 2.

Here is a transcription of the letter containing De Morgan’s solution to Problem 2, which he included in a letter [LB 170, [Nov. 1840], ff. 27r-27v]:

My dear Lady Lovelace,

I can soon put you out of your misery about p. 206. You have shown correctly that \(\phi(x+y)=\phi(x)+\phi(y)\) can have no other solution than \(\phi(x)=ax\), but the preceding question is not of the same kind; it is not show that there can be no other solution except \(\frac{1}{2} (a^x+a^{-x})\) but show that \(\frac{1}{2} (a^x+a^{-x})\) is a solution: that is, try this solution.

\[\begin{array}{rcl}\phi(x+y)&=&\frac{1}{2} (a^{x+y}+a^{-x-y} )\\
\phi(x-y)&=&\frac{1}{2} (a^{x-y}+a^{-x+y} )\\
          \phi(x+y)+\phi(x-y)&=&\frac{1}{2} (a^{x+y}+a^{-x-y}+a^{x-y}+a^{-x+y} )\end{array}\]

\[\begin{array}{ll}\mbox{[On the other hand]}\hspace{20pt}&    2\phi(x)\cdot \phi(y)=2\cdot \frac{1}{2} (a^x+a^{-x} )\cdot \frac{1}{2} (a^y+a^{-y} )\\
                                                            &     =\frac{1}{2} (a^x+a^{-x} )(a^y+a^{-y} )\\
                                                             & =\frac{1}{2} (a^{x+y}+a^{-x-y}+a^{x-y}+a^{-x+y} )\end{array}\]
the same as before.

To prove that this can be the only solution would be above you.

I think you have got all you were meant to get from the chapter on functions. The functional equations which can be fully solved are few in number.

Yours very truly
A De Morgan

Return to Main Solutions Page.
Continue to Solution to Problem 3.

Since \(\tan \theta=b/a\), Lovelace assumed that \(\sin⁡\theta=b\) and \(\cos⁡\theta=a\) in her attempt to solve Problem 3. However, \(\sin⁡\theta\) and \(\cos⁡\theta\) are actually equal to \(b/r\) and \(a/r\), respectively; so the expression Lovelace derived should have been
\[\begin{array}{lcl} (a+bk)^{m+nk}&=& r^{m+nk} (\cos⁡\theta+k \sin⁡\theta)^{m+nk}\\
&=&r^{m+nk}  (e^{k\theta})^{m+nk}\\
&=&r^{m+nk}\cdot e^{k(m\theta)} \cdot e^{-n\theta}\\
&=&r^m\cdot e^{-n\theta} \cdot r^{nk} \cdot e^{k(m\theta)}\\
&=&e^{m \log ⁡r-n\theta}\cdot e^{k(n \log ⁡r+m\theta)}\\
&=&e^A (\cos ⁡B + k \sin ⁡B ).\end{array}\]

Return to Main Solutions Page.
Continue to Solution to Problem 4.

Unfortunately, Lovelace’s work for Problem 4 no longer exists, but she probably attempted to solve it by a repeated application of the product rule. While there is nothing inherently wrong with this approach, it is clear that Peacock intended the problem to be solved using one of three theorems he stated in a footnote on the same page (see Figure 13). These theorems are simply three cases of what we nowadays call logarithmic differentiation, which can indeed simplify the process of differentiating products of multiple functions. But Lovelace was none the wiser, being completely mystified by the content of Peacock’s note: ‘Not one of the three theorems it contains is intelligible to me,’ she wrote [LB 170, 10 Nov. [1840], f. 63v].

Figure 13. Footnote on page 2 of George Peacock’s Collection of Examples of the Application of the Differential and Integral Calculus (1820).

If she had understood the meaning of these theorems, she could have applied theorem (2) to \(u=x^2  (a+x)^3  (b-x)^4\), where \(v_1=x^2\), \(v_2= (a+x)^3\), and \(v_3= (b-x)^4\). This would have given her
\[\begin{array}{ccl}du&=&x^2  (a+x)^3  (b-x)^4 \left \{\frac{2x}{x^2} + 3\frac{(a+x)^2}{(a+x)^3} - \frac{4(b-x)^3}{ (b-x)^4} \right \}dx \\
&=&x^2  (a+x)^3  (b-x)^4 \left \{\frac{2}{x}+\frac{3}{a+x}-\frac{4}{b-x}\right \}dx\\
&=&x^2  (a+x)^3  (b-x)^4 \left \{\frac{(2(a+x)(b-x)+3x(b-x)-4x(a+x)}{ x(a+x)(b-x)}\right \}dx\\
&=&x^2  (a+x)^3  (b-x)^4 \left \{\frac{2ab-6ax+5bx- 9x^2}{x(a+x)(b-x)}\right \}dx\\
&=&x (a+x)^2  (b-x)^3 (2ab-(6a-5b)x-9x^2 )dx.\end{array}\]
Thus Peacock’s answer was in fact correct.

Lovelace’s mistake was that she did not apply the chain rule to  \((b-x)^4\) correctly, and obtained \(4 (b-x)^3 \)instead of \(-4 (b-x)^3\). As De Morgan explained to her: ‘It is very common to suppose that if \(\phi(x)\) differentiated gives \(\psi(x)\), then \(\phi(-x)\) gives \(\psi(-x)\), but this should be \(\psi(-x)\times \mbox{diff. co.}(-x)\) or \(\psi(-x)\times -1\)’ [LB 170, 14 Nov. 1840, f. 20r]. Sure enough, once Lovelace rectified her mistake she obtained the correct answer.

Return to Main Solutions Page.
Continue to Solution to Problem 5.

To set up De Morgan's approach to solving Problem 5, let \(u\) be the product of \(n\) functions, \(f_1(x),f_2(x), \ldots ,f_n(x)\), where \(f_1(x)=f_2(x)=\ldots = f_n(x)=x\).  In other words, let \(u=x^n\).  Then using De Morgan’s version of Peacock’s Theorem 2:

\[\Large{ \begin{array}{lcl} \frac{du}{dx} &=& \frac{u}{f_1(x)}\cdot \frac{df_1}{dx} + \frac{u}{f_2(x)}\cdot\frac{df_2}{dx} + \frac{u}{f_3(x)}\cdot\frac{df_3}{dx} + \ldots + \frac{u}{f_n(x)}\cdot\frac{df_n}{dx} \\ \\  &=& \frac{x^n}{x }\cdot \frac{dx}{dx} + \frac{x^n}{x} \cdot \frac{dx}{dx} + \frac{x^n}{x} \cdot \frac{dx}{dx} + \ldots + \frac{x^n}{x} \cdot \frac{dx}{dx}\\ \\ &=& x^{n-1}+x^{n-1}+x^{n-1}+\ldots+x^{n-1}  \,\,\,\, (n \mbox{ times}) \\ \\ &=&nx^{n-1}. \end{array} }\]

Return to Main Solutions Page.
Continue to Solution to Problem 6.

In attempting to prove in Problem 6 that
\[\Large{\theta=\frac{\psi\left(\frac{\phi(a+h)-\phi(a)}{h}\right)-a}{h}}\]
De Morgan made the assumption that the function \(\phi'\) is always invertible in the domain under consideration. And as any good calculus student will know, this is by no means necessarily true.

Return to Main Solutions Page.
Continue to Solution to Problem 7.

In trying to solve the differential equation in Problem 7, \[\frac{dy}{dx}=\frac{y}{x},\] Lovelace’s reasoning was that, since the derivative \(dy/dx\) is a limit, and since a limit is a ‘constant \& fixed thing’, this must imply that the ratio \(y/x\) is also a constant. Calling this constant \(a\) would mean that \[\frac{y}{x}=a\] or \[y=ax.\]

But of course the flaw in this argument is that limits of functions are not in general equal to constants. Indeed, taking the standard definition of the derivative as \[f'(x) = \lim_{h \rightarrow 0}\frac{f(x+h)-f(x)}{h}\] we can see that, while the quantity \(h\) approaches zero, the variable \(x\) is free to assume any value whatsoever—quite the opposite of a constant.

The simplest method for solving the equation correctly would be to separate the variables and integrate, giving \[\int \frac{dy}{y} =\int \frac {dx}{x}\] or \[ \log ⁡ y = \log ⁡x+c,\] which, letting \(a=e^c\), is \[y=ax.\]

Return to Main Solutions Page.
Continue to Solution to Problem 8.

In the 19th century, the word ‘impossible’ was widely used in the way that ‘imaginary’ is employed by mathematicians today, with real numbers often referred to as ‘possible’. Thus, in claiming in connection to Problem 8 that the expression
\[\int \frac{dx}{x^2-c} = \frac{1}{2\sqrt{c}} \log⁡\left(\frac{\sqrt{c}-x}{\sqrt{c}+x}\right )\] ‘becomes impossible when \(x\) is greater than \(\sqrt{c}\),’ De Morgan merely meant that when the integrand is positive, the logarithm on the right will become a logarithm of a negative number, and hence imaginary, or more accurately, complex. Lovelace’s first mistake was therefore to have misinterpreted the term ‘impossible quantity’ to mean something meaningless or illogical. As she said:

I fancy I had a little misunderstood the mathematical meaning of the words impossible quantity. I have loosely interpreted it as being equivalent to ‘an absurdity’ [LB 170, 21 Aug. [1841], f. 122r].

Her second mistake was to have assumed in the standard definition of a logarithm with base \(a\), that \(a\) could be positive or negative. Thus, if a logarithm happened to be odd, she inferred that its base could be negative, a circumstance which, she speculated, ‘would I think be admitted theoretically (tho' inconvenient practically) on the common beginner's introduction on the Theory of Logarithms. Am I right?’ [LB 170, 21 Aug. [1841], f. 122r]. A cursory glance at page 224 of De Morgan’s Elements of Algebra—which, as the letters attest, she had certainly read—reveals that the answer to this question is no!

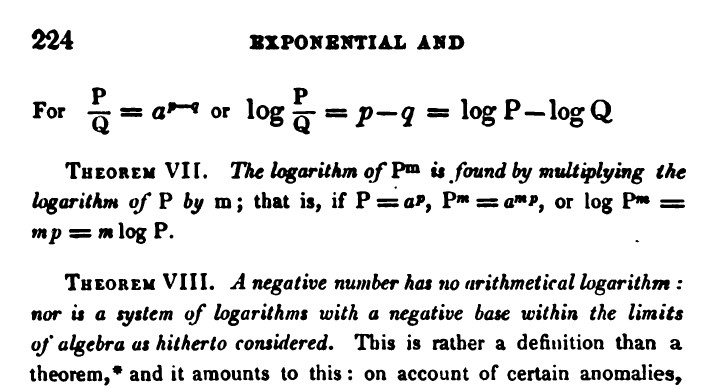
Figure 14. Theorem VIII on page 224 of De Morgan’s Elements of Algebra
states that logarithms cannot have a negative base.

Return to Main Solutions Page.
Continue to Solution to Problem 9.

Since  \(y^2=2ax+x^2=(2a+x)x\) in Lovelace's approach to Problem 9,  using the product rule we have   \[ydy=(x+a)dx    \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,            [2]\] so that \[(x+a)dy+ydy=(x+a)(dx+dy)\] or \[(x+a+y)dy=(x+a)(dx+da+dy)\] and thus \[\frac{dy}{x+a} = \frac{d(x+a+y)}{x+a+y}.\] Now since, by [2], \[\frac{dy}{x+a}=\frac{dx}{y}\] this means that \[\frac{dx}{y}=\frac{d(x+a+y)}{x+a+y}.\] So, recalling that \(y^2=2ax+x^2\), we have \[\int \frac{dx}{\sqrt{2ax+x^2}} = \log⁡(x+a+\sqrt{2ax+x^2}) = \log\left (\frac {x}{2} +\frac{a}{2} + \frac{\sqrt{2ax+x^2}}{2} \right )+ \log ⁡2\] which is Lovelace’s result.

Now recall that De Morgan had obtained \[\int \frac{dx}{\sqrt{2ax+x^2}} = \log⁡(x+a+\sqrt{2ax+x^2}) + \log ⁡2.\] Strictly speaking, his result should read \[\int \frac{dx}{\sqrt{2ax+x^2}} = \log⁡(2x+2a+2\sqrt{2ax+x^2}) +C\] and Lovelace’s result should be \[\int \frac{dx}{\sqrt{2ax+x^2}} = \log⁡(x + a +\sqrt{2ax+x^2}) +C'.\] Thus, letting Lovelace’s constant of integration \(C'=C+\log ⁡2\) reveals that the two results are equivalent and also explains De Morgan’s remark that the \(\log 2\), ‘being a Constant, matters nothing.’

Return to Main Solutions Page.
Continue to Solution to Problem 10.

To reconcile the solutions to Problem 10 given by Lovelace and De Morgan, how can the solution \[u=C \sin⁡\theta+C'  \cos⁡\theta+\frac{1}{2} \theta \sin ⁡\theta+ \frac{1}{4} \cos⁡\theta\] be converted into its final form \[u=C \sin⁡\theta+C'  \cos⁡\theta+\frac{1}{2} \theta \sin⁡\theta ?\] As Lovelace suggested, substituting \(\theta=\frac{\pi}{2}\) would obviously eliminate the \(\frac{1}{4} \cos⁡\theta\) term, but that clearly would not be correct as the other terms would also be changed. Why then does the \(\frac{1}{4} \cos⁡\theta\) disappear?

The answer lies in the fact that the two \(\cos⁡\theta\) terms both have constant coefficients, namely, \(C'\)  and  \(\frac{1}{4}\). They can thus be combined into a single term \[\left(C'+\frac{1}{4}\right)  \cos⁡\theta\] or \[C'' \cos⁡\theta\] where \(C''=C'+\frac{1}{4}\). Thus De Morgan’s final answer, while not wrong, is slightly misleading, since in light of the above discussion it would be better expressed as \[u=C \sin⁡\theta+C'' \cos⁡\theta+ \frac{1}{2} \theta \sin⁡\theta.\]

Return to Main Solutions Page.