We begin with a very simple problem. For any student intending to study higher mathematics, the ability to manipulate and re-arrange algebraic expressions is essential. However, this is a skill that does not necessarily come easily to all students, and at first Ada Lovelace also found it difficult, as we saw in her questions to Mary Somerville. Her problems with symbolic manipulation are further evident in her correspondence with De Morgan, particularly early on in her studies. In one letter, from November 1840, she noted how difficult she found trying to verify a relatively simple point in algebra.

Figure 7. Extract from page 226 of De Morgan’s Elements of Algebra (2nd ed., 1837).

The problem arose from a discussion concerning logarithmic expressions in De Morgan’s Elements of Algebra. As can be seen from Figure 7, at the bottom of page 226 De Morgan made a simple substitution, letting

\[\frac{1+b}{1-b}=\frac{1+x}{x}\]

which he said resulted in

\[b=\frac{1}{2x+1}.\]

Lovelace had two problems with De Morgan’s claim [LB 170, 10 Nov. [1840], ff. 64r-64v]:

In the first place I do not feel satisfied that the form \(\frac{1+b}{1-b}\) is capable of being changed into the form \(\frac{1+x}{x}\). There are three suppositions we may make upon it, (supposing that it is capable of this second form).  \(x\) may be less than \(b\), in which case the denominator must also be less than \(1-b\), and less in a certain given proportion, in order that the Fractional Expression may remain the same.  \(x\) may \(=b\), in which case the second form can only be true on the supposition that \(1-b=x=b\), or \(b=\frac{1}{2}\).  \(x\) may be greater than \(b\), in which case the denominator of the second form must also be greater than \(1-b\), in a certain given proportion, in order that the Fractional expression may remain the same.

I will leave it to the reader to determine whether her three suppositions are correct. However, it is Lovelace’s second issue that was of more concern [LB 170, 10 Nov. [1840], ff. 64v-65r]:

But secondly supposing \(\frac{1+b}{1-b}\) to be under all circumstances susceptible of the form \(\frac{1+x}{x}\), I cannot deduce from this equation \(b=\frac{1}{2x+1}\).

In other words, given the equation \[\frac{1+b}{1-b}=\frac{1+x}{x}\] Lovelace was unable to re-arrange it to solve for \(b\). This was clear evidence that there were significant gaps in her mathematical knowledge and De Morgan was quick to warn her of the periodic digressions into more elementary mathematics that would be required to fill them: ‘You understand of course that your Differential Calculus must be delayed from time to time while you make up those points of Algebra and Trigonometry which you have left behind’ [LB 170, 27 Sept. 1840, f. 16r]. And in a subsequent letter, he explained how to solve the problem. You can see his solution here.

Return to Main Problems Page.
Continue to Problem 2.

Here is another algebraic problem with which Lovelace had trouble. At around the same time as the previous problem, she was struggling with the topic of functional equations, introduced in Chapter 10 of De Morgan’s Algebra. Given a particular general equation, the goal was to find the function or functions that satisfied it. On November 27, 1840, Lovelace wrote to De Morgan about the exercise in Figure 8. (Note that the functional expression \(\phi x\) means what we would write as \(\phi(x)\), or \(f(x)\), today.)

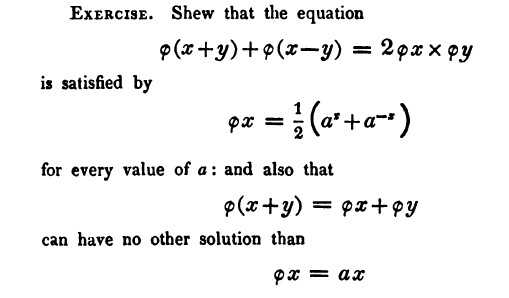
Figure 8. Exercise from p. 206 of De Morgan’s Elements of Algebra.

Lovelace was actually able to solve the second part of the problem relatively easily, since it is quite straightforward to use \(\phi(x+y)=\phi(x)+\phi(y)\) to prove that \(\phi(ax)=a\phi(x)\) and thus that \(\phi(x)\) is a linear function with \(\phi(0)=0\). But she described herself as being ‘completely baffled’ by the first part of the exercise. In a much quoted passage, she wrote:

I do not know when I have been so tantalized by anything, & should be ashamed to say how much time I have spent upon it, in vain. These Functional Equations are complete Will-o’-the-Wisps to me. The moment I fancy I have really at last got hold of something tangible & substantial, it all recedes further & further & vanishes again into thin air [LB 170, 27 Nov. [1840], ff. 149r-149v].

Starting with
\[\phi(x+y)+\phi(x-y)=2\phi(x)\phi(y)\]
she first obtained \[2\phi(x)=\frac{\phi(x+y)+\phi(x-y)}{\phi(y)}.\]
She then continued [LB 170, 27 Nov. [1840], f. 149v]:

Since \(x\) and \(y\) may have any values whatever, (at least such I conclude is of course intended), let \(y=0\). We have then
\[\begin{array}{c}2\phi(x)=\frac{\phi(x)+\phi(x)}{\phi(0)}\\
\therefore 2\phi(x)\times \phi(0)=\phi(x)+\phi(x)\\
\mbox{ or } 2\phi(x)\times \phi(0)=2\phi(x).\end{array}\]

She thus concluded (correctly) that \(\phi(0)=1\), but then claimed (incorrectly) that this was equal to \(a^0\), ‘since \(a^0\) is the only function of \(0\) which can \(= 1\)’. (The reader will of course be able to spot the flaw in her reasoning.) ‘I think so far is correct in itself,’ she wrote, ‘but whether it be the right road to the rest is another question’ [LB 170, 27 Nov. [1840], ff. 149v-150r].

Unfortunately, she did not turn out to be on the right track and after detailing a few other erroneous attempts, she gave up:

In short, many & various are the experiments I have made, but I will not detail any more. Indeed I think you may be possibly heartily sick of what I have detailed. But I wished to show you that I have not failed from want of trying, at least; & also to give you the chance of smiling at my expence [sic] [LB 170, 27 Nov. [1840], f. 151r].

Interestingly, the chief reason for Lovelace’s difficulty in this algebraic problem is completely different from that encountered in Problem 1. This time, it was not her ability to manipulate algebraic expressions that held her back, but rather a misunderstanding of what the question actually wanted her to do. Whereas the second part (which she answered correctly) wanted her to show that the functional equation led only to the result that \(\phi(x)=ax\), the first part merely required her to plug \(\phi(x)=\frac{1}{2 }(a^x+a^{-x})\) into the first equation to verify that it was satisfied.

Not long afterwards, De Morgan wrote to Lovelace to ‘put you out of your misery’ about this problem, and gave his solution in a few lines.

Return to Main Problems Page.
Continue to Problem 3.

Lovelace was no stranger to matters concerning complex and imaginary numbers. Nevertheless, the next problem showed that, despite her familiarity with them, her algebraic skills still needed improvement. While reading an article in the Penny Cyclopaedia by De Morgan on “Negative and Impossible Quantities”,⁴ she came across the following passage [De Morgan 1840, 134]:

It can be easily shown that any algebraical expression, however complicated, which is a function of \(\sqrt{(-1)}\) can be reduced to the form \(A+B\sqrt{(-1)}\), where \(A\) and \(B\) are possible quantities. For instance (\(k\) being \(\sqrt{(-1)}\) \[ (a+bk)^{m+nk}=e^A  \cos⁡ B+k e^A  \sin⁡ B \,\,\,\,\,\,\,\,   [1]  \]
where \(A\) and \(B\) are determined as follows. Let \[r=\sqrt{(a^2+b^2)},  \,\, \mbox{ [and] } \,\,  \tan\theta=\frac{b}{a}, \,\, \mbox{[then]} \] \[A=m \log ⁡r-n\theta, B=n \log r⁡   +m\theta.\]

In a letter to De Morgan, Lovelace reported [LB 170, 9 Sept. [1841], f. 123r] that she had ‘tried a little to demonstrate this Formula’ (i.e. [1]), but was having trouble. Based on the assumption that \(\tan⁡ \theta=\frac{b}{a}\)  gives \(\sin⁡ \theta=b\) and \(\cos⁡\theta=a\), she obtained

\[\begin{array}{rcl}
(a+bk)^{m+nk}&=& (\cos⁡ \theta+k \sin⁡\theta)^{m+nk}\\
&=&\left (e^{k\theta} \right)^{m+nk}\\
&=&e^{k(m\theta)}\times \{(e^{k(n\theta)} )\}^k \\
&=&(\cos ⁡m\theta+k \sin ⁡m\theta )\times (\cos ⁡n\theta+k \sin ⁡n\theta)^k.\end{array}\]

However, since she could get no further, she believed that the complete demonstration ‘must be a very complicated process’ [LB 170, 9 Sept. [1841], f. 123v]. In fact, she was closer than she realized but, despite a clear working knowledge of the algebra of exponents, and indeed Euler’s Formula, it was again her lack of algebraic and trigonometric experience (and consequent intuition) that ultimately prevented her from obtaining the desired result.

Can you spot Lovelace’s mistake and prove formula [1]? Click here to see the proof.

Return to Main Problems Page.
Continue to Problem 4.

Notes

4. The phrase ‘impossible quantity’ was commonly used at this time to mean an imaginary or complex number.

Moving now to calculus, one of the first books De Morgan recommended that Lovelace should study was George Peacock’s Collection of Examples of the Application of the Differential and Integral Calculus, which contained a host of problems and their solutions for students to practice. One of the first problems in the book was to find the differential (not the derivative) of \(u=x^2(a+x)^3(b-x)^4\) [Peacock 1820, 2]. When attempting this question, Lovelace obtained
\[du=\{2ab-(6a-5b)x-x^2 \}x(a+x)^2(b-x)^3 dx\]
whereas the book gave
\[du=\{2ab-(6a-5b)x-9x^2 \}x(a+x)^2(b-x)^3 dx\]
`& I am inclined to think it is a misprint in the latter’ [LB 170, 10 Nov. [1840], f. 63r].

Figure 9. George Peacock (1791–1858), frontispiece of Alexander Macfarlane’s
1916 Lectures on Ten British Mathematicians of the Nineteenth Century.

So who was correct, Lovelace or Peacock?

Return to Main Problems Page.
Continue to Problem 5.

Lovelace also tried her hand at proving standard results in calculus, such as the general power rule, namely that \[\frac{d}{dx} (x^n )=nx^{n-1}.\]

The method she used, which was correct, was to find the difference quotient \[\frac{(x+\theta)^n-x^n}{\theta},\] then use the binomial theorem to expand \((x+\theta)^n\), cancel the appropriate terms, and take the limit as \(\theta \rightarrow 0\). ‘It strikes me,’ she told De Morgan, ‘as having the advantage in simplicity, & in referring to fewer requisite previous Propositions’ [LB 170, 10 Jan. [1841], f. 82v].

Her proof was perfectly sound, but there was one small problem—its reliance on the binomial theorem. She had learnt that theorem from De Morgan’s Elements of Algebra, in which the generally accepted proof of the time was given. Unfortunately, that proof relied on a lemma which stated that: \[\lim_{w\rightarrow v}⁡\frac{v^n-w^n}{v-w}= nv^{n-1}.\] As De Morgan was quick to point out, ‘if you take the common proof of the binomial theorem, you are reasoning in a circle, for that proof requires that it should be shown that \(⁡\frac{v^n-w^n}{v-w}\) has the limit \(nv^{n-1}\) as \(w\) approaches \(v\). This is precisely the proposition which you have deduced from the binomial theorem’ [LB 170, [Jan. 1841], f. 34r]. A few days later, Lovelace acknowledged that ‘my proof of the limit for the function \(x^n\) is a piece of circular argument’ [LB 170, 17 Jan. [1841], f. 85v]. As she explained: ‘It had not struck me that, calling \((x+\theta)=v\), the form \(\frac{(x+\theta)^n-x^n}{\theta}\) becomes \(\frac{v^n-x^n}{v-x}\) ’ [LB 170, [Jan. 1841], f. 91r].

As an exercise, instead of using Lovelace’s method, try proving the general power rule the way De Morgan did it (for positive integer values of \(n\)). He used a result equivalent to Theorem 2 from Peacock’s Collection of Examples (see Figure 13) [De Morgan 1836-42, 51]:

If \(u\) be the product of n functions \(PQR\ldots \) then the product of all but \(P\) is \(u/P\), and so on; whence we have \[\frac{du}{dx}=\frac{u}{P}\frac{dP}{dx}+\frac{u}{Q} \frac{dQ}{dx}+\frac{u}{R} \frac{dR}{dx}+ \ldots \]

You can check your proof here.

Return to Main Problems Page.
Continue to Problem 6.

Another indispensable result in calculus is the Mean Value Theorem, which states that if a function \(f\) is continuous on a closed interval \([a,b]\) and differentiable on \((a,b)\), then there exists a value \(c\) in \((a,b)\) such that

\[\frac{f(b)-f(a)}{b-a}=f'(c).\] In his Differential and Integral Calculus, De Morgan stated it in the following form [De Morgan 1836–42, 67]:

\(\ldots\) between \(a\) and \(a+h\) \(\ldots\) it follows that \[\frac{\phi(a+h)-\phi(a)}{h}=\phi'(a+\theta h)\] is true for some positive value of \(\theta\) less than unity.

Recognizing that \(a+h=b\) and \(a+\theta h=c\in(a,b)\), since \(0<\theta<1\), it is clear that De Morgan’s statement is basically equivalent to the modern-day formulation. While Lovelace had no problem with his statement of the theorem itself, she was puzzled by his assumption that \(\theta\) was a function of \(a\) and \(h\), writing: ‘I see neither the truth of this assertion, nor do I perceive the importance of it (supposing it is true) to the rest of the argument’ [LB 170, 19 Feb. [1841], f. 100r].

De Morgan replied by asking her, rhetorically: ‘Why should \(\theta\) be independent of \(a\) and \(h\) [since] we have never proved it to be so’? [LB 170, [22 Feb. 1841], f. 42v] To demonstrate that \(\theta\) could be expressed as a function of the two values as he claimed, he let \(\psi\) be the inverse function of \(\phi'\) so that \(\psi(\phi'(x))=x\). Then, he wrote:

\[\begin{array}{l}
\frac{\phi(a+h)-\phi(a)}{h}=\phi'(a+\theta h)\\ \\
\psi \left (\frac{\phi(a+h)-\phi(a)}{h} \right )=\psi(\phi'(a+\theta h)))=a+\theta h\\ \\
\theta =\frac{ \psi \left (\frac{\phi(a+h)-\phi(a)}{h} \right ) - a}{h} \left \{\mbox{Say that this is not a function of \(a\) and \(h\), if you dare} \right .\end{array}\]

Convincing though this demonstration may seem, it turns out that Lovelace’s doubts about the validity of De Morgan’s assertion were well founded. In fact, the professor was actually incorrect: \(\theta\) is not necessarily a function of \(a\) and \(h\), and the above proof is wrong. The question is: why?

Return to Main Problems Page.
Continue to Problem 7.

Let’s move on to questions involving integration, or at least, questions that should involve integration, such as the solution of first-order differential equations. In July 1841, De Morgan posed the following problem to Lovelace:

Try to prove the following. It is only when \(y=ax\) (\(a\) being constant) that \[\frac{dy}{dx}=\frac{y}{x}\]  [LB 170, 11 July [1841], f. 112v].

In her answer, Lovelace employed a heuristic (and flawed) approach, relying on intuitive ideas about limits and derivatives (or as they were then known, ‘differential coefficients’), rather than the correct method, which required integration. But it is clear that her confidence in it was not strong: ‘I do not feel quite sure that my proof is a proof. But I think it is too’ [LB 170, 11 July [1841], f. 112v]. This was her argument:

Given as \(\frac{dy}{dx}=\frac{y}{x}\), what conditions must be fulfilled in order to make this equation possible? Firstly: I see that since \(\frac{dy}{dx}\) means a Differential Co-efficient, which from it's [sic] nature (being a Limit) is a constant & fixed thing, \(\frac{y}{x}\) must also be a constant & fixed quantity. That is \(y\) must have to \(x\) a constant Ratio which we may call \(a\). This seems to me perfectly valid. And surely a Differential Co-efficient is as fixed & invariable in it's [sic] nature as anything under the sun can be [LB 170, 15 Aug. [1841], ff. 116r-116v].

But it wasn’t long before she realized that this argument was flawed. What was the error in her reasoning? And how should this problem be solved?

Return to Main Problems Page.
Continue to Problem 8.

Here’s another problem that involves an integral. First of all, prove for yourselves that \[\int \frac{dx}{x^2-c}=\frac{1}{2\sqrt{c}} \log⁡\left (\frac{\sqrt{c}-x}{\sqrt{c}+x}\right )\] plus a constant, of course. De Morgan gave this result on pages 112–3 of his Differential and Integral Calculus, where he stated that it ‘becomes impossible when \(x\) is greater than \(\sqrt{c}\), for in that case the integral becomes the logarithm of a negative quantity’ [De Morgan, 1836-42, 113].

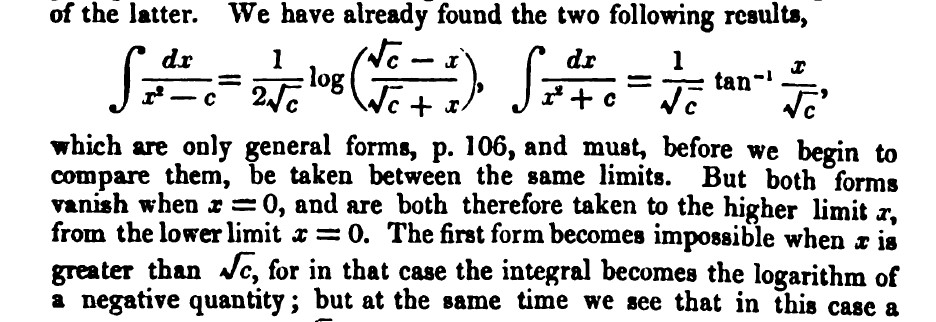
Figure 10. Part of page 113 from De Morgan’s Differential and Integral Calculus.

But Lovelace took issue with this claim. In a letter of August 1841, she observed that ‘there are surely certain cases in which negative quantities may be powers, & therefore may have Logarithms’. Thus, since, for example,  \[-a^3=(-a)\times(-a)\times(-a),\] ‘\(3\) is here surely the Logarithm of a Negative Quantity. Similarly a negative quantity multiplied into itself any odd number of times will give a negative result’ [LB 170, 15 Aug. [1841], f. 116r].

Lovelace has made two mistakes here. What were they?

Return to Main Problems Page.
Continue to Problem 9.

The integral \[\int \frac{dx}{\sqrt{A+Bx+Cx^2}}\] is more sophisticated still. Try to prove for yourself that, if \(C>0\), \[\int \frac{dx}{\sqrt{A+Bx+Cx^2}}= \frac{1}{\sqrt{C}} \log\left ( 2Cx+B+\sqrt{4C(A+Bx+Cx^2)} \right ).\] In his Calculus, letting \(A=0\), \(B=2a\), and \(C=1\), De Morgan deduced that, as he put it: \[\int \frac{dx}{\sqrt{2ax+x^2}}= \log \left( x + a + \sqrt{(2ax+x^2)} \right ) + \log ⁡2. \mbox{ (Omit the constant.) } \]

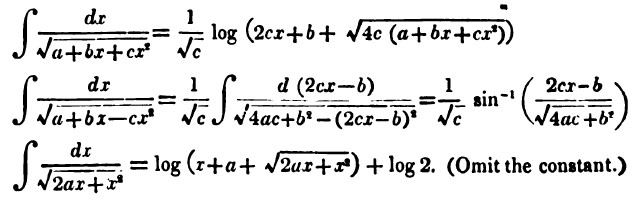
Figure 11. Part of page 116 from De Morgan’s Differential and Integral Calculus.

But when Lovelace tried to derive this result from first principles, she wrote [LB 170, 15 Aug. [1841], f. 115v]:

I cannot make it anything but \[\int \frac{dx}{\sqrt{2ax+x^2}} = \log \left ( x + 2a + \sqrt{(2ax+x^2)} \right )\] or else \[ = \log \left ( \frac{x}{2} + a + \frac{\sqrt{2ax+x^2}}{2} \right )+ \log 2⁡  \] \(\ldots\)  and I begin to suspect the book.

Her approach was straightforward. Setting \(2ax+x^2=(2a+x)x=y^2\), she derived the differential equation \((2a+x)dx=ydy\), from which she formed the integral \[\int  \frac{dx}{y}=\int \frac{dy}{2a+x}  .\]

Then, by analogy with the ‘fact’ that \(\frac{dx+dy}{x+y}=\frac{dx}{y}\), she obtained \[ \begin{array}{lcl} \int \frac{dx}{y} &=&  \int \frac{d(2a+x)+dy}{(2a+x)+y}\\ &=&\int \frac{d(2a+x+y)}{2a+x+y}\\ &=&\log⁡(2a+x+y)\\ &=&\log⁡(2a+x+\sqrt{2ax+x^2})\\ &=& \log⁡\left ( \frac{x}{2} + a + \frac{\sqrt{2ax+x^2}}{2}\right )+\log ⁡2.\end{array}\]

In addition to her erroneous assumption that \[\frac{dx+dy}{x+y}=\frac{dx}{y}\]

De Morgan was able to spot that, given \(y^2=(2a+x)x\), she had forgotten to apply the product rule, so that her differential equation should have been \[ydy=\frac{1}{2} xdx + \frac{1}{2} (2a+x)dx \] or   \[ydy=(x+a)dx.\,\,\,\,\,               \mbox{[2]}\] After correcting these errors, Lovelace wrote in a subsequent letter [LB 170, 21 Aug. [1841], f. 121v], that

we arrive then in my corrected paper, at \[\begin{array}{rcl}\int \frac{dx}{\sqrt{2ax+x^2}} &=& \log \left( x + a + \sqrt{(2ax+x^2)} \right )\\ &=&\log⁡\left( \frac{x}{2} + \frac{a}{2} + \frac{\sqrt{2ax+x^2}}{2} \right )+\log ⁡2.\end{array}\]

Can you derive Lovelace’s final result from equation [2]?

In his acknowledgement, De Morgan observed that Lovelace’s answer agreed with his result in all respects ‘but the log 2, which being a Constant, matters nothing’ [LB 170, 21 Aug. [1841], f. 121v]. Explain why his and Lovelace’s results are equivalent.

Return to Main Problems Page.
Continue to Problem 10.

Our final problem comes close to the end of Lovelace’s correspondence course with De Morgan. By early November 1841, she had progressed to the subject of second-order differential equations. One of the examples with which she had trouble was on page 156 of De Morgan’s Calculus. Given the nonhomogeneous equation

\[\frac{d^2 u}{d\theta^2 }+u=\cos⁡\theta\]

De Morgan gave its general solution as

\[u=C \sin ⁡\theta + C' \cos⁡ \theta + \sin⁡\theta \int cos^2 \theta d \theta - \frac{1}{2}  \cos⁡ \theta \int \sin ⁡2\theta  d\theta,\] which, since

\[ \int \cos^2 \theta d\theta = \frac{1}{2} \theta + \frac{1}{4} \sin 2 ⁡  \theta \, \,   \mbox{ and  } \,\, \int \sin ⁡2\theta  d\theta = -\frac{1}{2} \cos ⁡2\theta \] resulted in

\[u=C \sin\theta  + C' \cos⁡ \theta +\frac{1}{2}\theta \sin⁡ \theta + \frac{1}{4}  \sin ⁡2 \theta  \sin⁡ \theta+  \frac{1}{4} \cos⁡\theta  \cos ⁡2\theta.\] Using double angle formulae, he converted this into

\[u=C \sin⁡ \theta + C'  \cos⁡ \theta + \frac{1}{2}\theta \sin \theta+ \frac{1}{4}  \cos⁡ \theta,\] which he then expressed in its final form as

\[u=C \sin⁡ \theta+C'  \cos⁡ \theta + \frac{1}{2} \sin⁡ \theta,\] along with a challenge: ‘Explain this step?’ (See Figure 12).

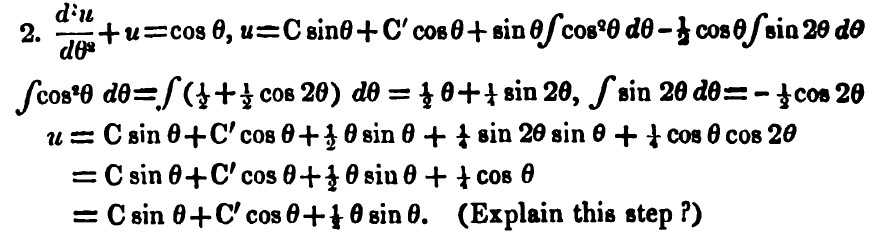
Figure 12. Problem from page 156 of De Morgan’s Differential and Integral Calculus.

The trouble was, as Lovelace remarked in a letter to De Morgan, ‘I cannot “explain this step”.’ She noted that ‘in the previous line, we have:   \[\begin{array}{r}  (1) \ldots u = C \sin⁡  \theta +C'  \cos⁡ \theta + \frac{1}{2}\theta  \sin⁡ \theta + \frac{1}{4} \cos \theta ⁡\mbox{ (quite clear)} \end{array}\]   \[\begin{array}{rcl}  (2) \ldots  \mbox{ And }  u &=&\cos⁡ \theta -\frac{d^2 u}{d \theta ^2 } \mbox{ (by hypothesis)} \\                                                             &=& \frac{1}{4}  \cos⁡ \theta+\left (\frac{3}{4} \cos⁡ \theta-\frac{d^2 u}{d\theta^2} \right ) \end{array}\]

whence one may conclude that \[C \sin⁡\theta+C'  \cos⁡ \theta + \frac{1}{2}\theta\sin⁡ \theta=\frac{3}{4}\cos⁡ \theta-\frac{d^2 u}{d\theta^2} \] But how \(u=C \sin⁡  \theta+C'  \cos⁡  \theta+\sin⁡\theta\cdot\frac{1}{2} \theta\) is to be deduced I do not discover.’ [LB 170, 4 Nov. [1841], ff. 132v-133r]

Not deterred, she tried again:

By subtracting \(\frac{1}{4}\cos⁡ \theta\)  from both sides of (1), we get \[u-\frac{1}{4} \cos⁡ \theta= C \sin⁡ \theta+C' \cos⁡ \theta+ \frac{1}{2} \theta \sin⁡ \theta\] But unless \(\frac{1}{4} \cos⁡ \theta=0\), (which would only be the case I conceive if \(\theta=\pi/2\)), I do not see how to derive the equation \(\ldots\) [LB 170, 4 Nov. [1841], f. 133r].

De Morgan’s final solution is certainly correct. So can you explain why the \(\frac{1}{4} \cos⁡ \theta\) mysteriously disappears?

Return to Main Problems Page.
Continue to Main Solutions Page.