Algebra Tiles Explorations of al-Khwārizmī's Equation Types: Modeling the Compound Equations and the Moiety Principle
This section focuses on modeling the three compound species in al-Khwārizmī’s algebra text using a step-by-step problem-solving approach, with each case treated in a separate subsection:
- Type 4: roots and squares = numbers
- Type 5: squares and numbers = roots
- Type 6: squares = roots and numbers
As al-Khwārizmī noted, the three basic equations (Types 1-2-3) discussed in the previous section “do not require that the roots be halved” [Rosen 1831, 13]. In the latter three (Types 4-5-6), on the other hand, he asserted that “halving the roots is necessary” [Rosen 1831, 13]. The utilization of moities is thus also a key feature in modeling the solutions of equations of Types 4-5-6 using algebra tiles representations. He also provided geometric constructions (based on specific equation examples) for each of these three equation types “to point out the reasons for halving” [Rosen 1831, 13]. For equations of Types 5 and 6, the diagrams that accompany these synthetic constructions are not transferrable to an algebra tile representation. As indicated by Figure 2, however, the second diagram that al-Khwārizmī gave in his demonstration for Type 4 equations (based on the example \(x^2+10x = 39\)) is reminiscent of the algebra tile models we provide in this section. Notice in particular the small square of area 25 in the lower left-hand corner, which represents the final step in the "Completing the Square" technique for solving this equation. In fact, similar diagrams are widely used with an equation of Type 4 to illustrate that solution technique.
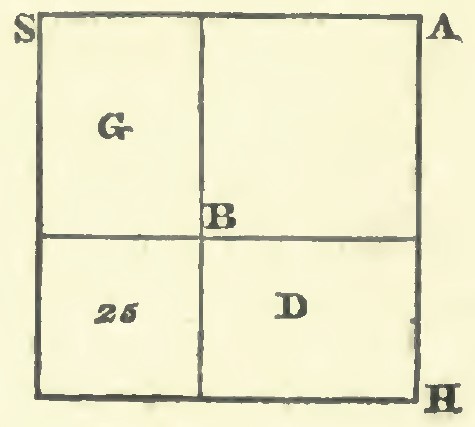
Figure 2. Second diagram in al-Khwarizmi's geometric demonstration of Type 4
using the equation “a Square and twenty-one Dirhems are equal to ten Roots” [Rosen 1831, 16].
Algebra Tiles Explorations of al-Khwārizmī ’s Equation Types: Roots and Squares are Equal to Numbers
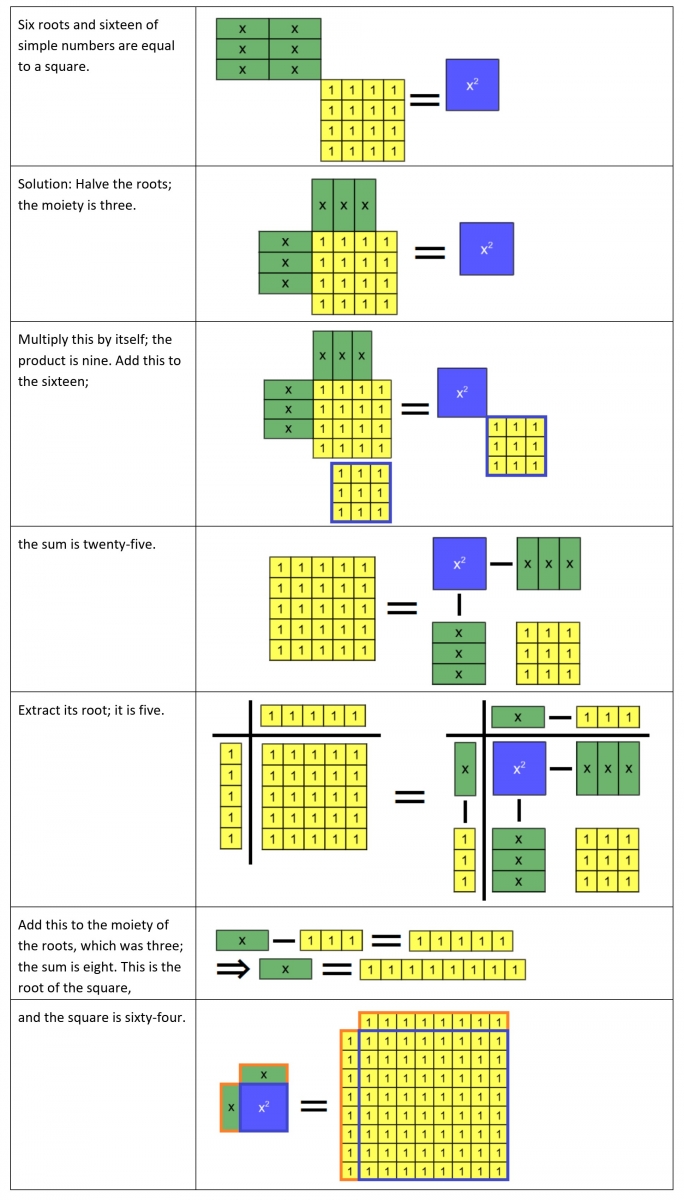
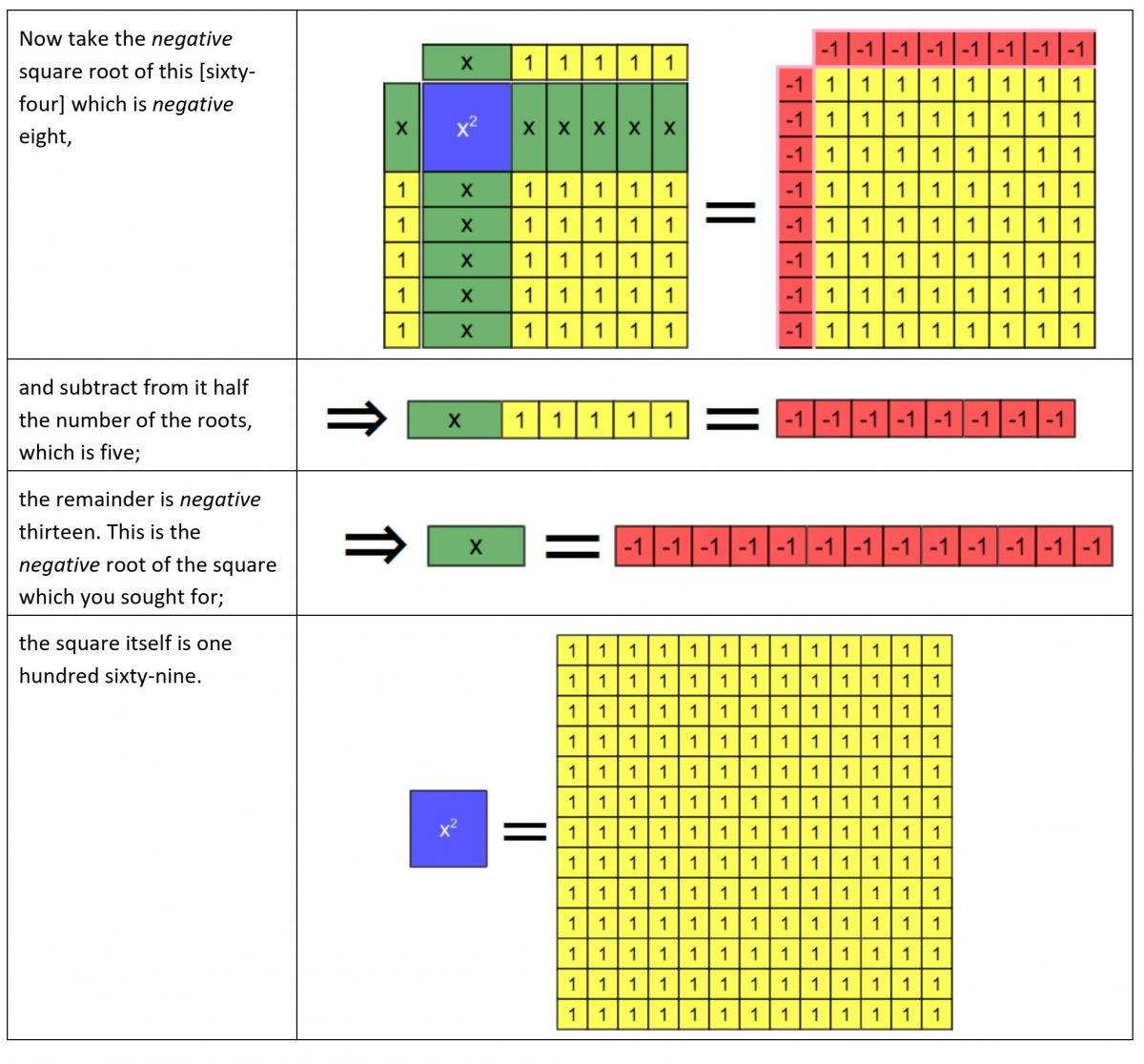
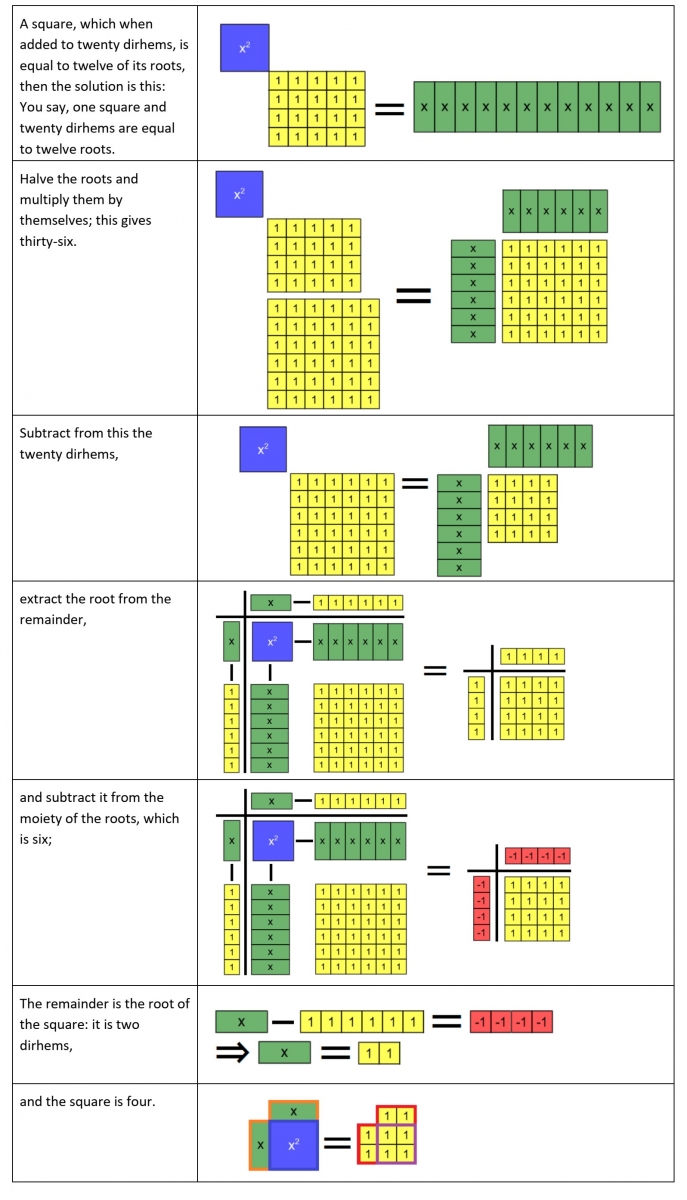
In our example for this case (taken from [Rosen 1831, 8]), we first model al-Khwārizmī’s procedure for producing the positive root of the given quadratic. We then illustrate how the use of algebra tiles suggests a modification of that procedure that produces the negative root. Here and in our other examples of compound species, it is important for students to be aware that whenever al-Khwārizmī added a quantity associated with one side of an equation (e.g., the second step of Example 7a), it is implied by the algebra tile representation that the same quantity is added to the other side as well. A classroom discussion of why this is necessary in the algebra tile representation, and also why it is not needed in al-Khwārizmī’s verbal description of his procedure, could be fruitful with prospective teachers.
Example 7a: Roots and Squares are Equal to Numbers (Type 4), positive solution

The procedure for obtaining the negative solution was not discussed in al-Khwārizmī’s solution, due to the restrictions in his number system that were mentioned in the last section. Below, we show a procedure for obtaining the negative solution by involving negative tiles to represent the extraction of a negative square root.
Example 7b: Roots and Squares are Equal to Numbers (Type 4), negative solution
Algebra Tiles Explorations of al-Khwārizmī ’s Equation Types: Squares and Numbers are Equal to Roots
Equations of Type 5 (squares + numbers = roots) have presented the most challenging task in terms of accurate representation of al-Khwārizmī’s verbal descriptions with algebra tiles.3 We thus offer two alternatives for modeling al-Khwārizmī’s first example of this case (taken from [Rosen 1831, 11–12]). Unlike equations of Type 4, it is unlikely that all students will come up with either alternative on their own. After allowing for a period of open exploration (either individually or in small groups), the instructor could illustrate one or both of these modeling alternatives (or offer hints as to how students can get started on each). A classroom discussion of the pros and cons of these different approaches could also be of interest.
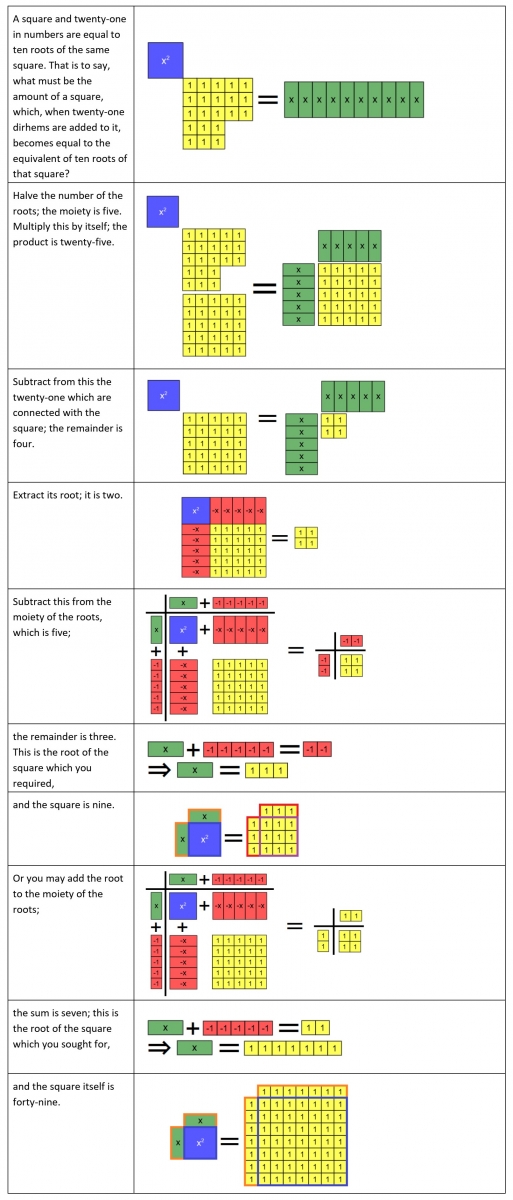
Example 8a shows the first approach to modeling of al-Khwārizmī’s instructions for this case, where we have enumerated the solution steps for the purpose of discussing the case’s complexities. In this approach, there are two steps where the algebra tile representation includes operations or objects that are not part of al-Khwārizmī’s verbal instructions. First, in Step 3, I simultaneously felt the need to subtract "\(10-x\)" from both sides while extracting the root of \(4\). This transforms the left-hand side (LHS) into a binomial rectangle with \(x-5\) and \(x-5\) as dimension tiles. Then, in Step 4, I made the adjustment of considering the number 4 of the right-hand side (RHS) to be the square of \(-2\), in accordance with the phrase “Subtract this [root of four] from the moiety of the roots, which is five; the remainder is three” [emphasis added]. Otherwise (that is, if the number \(4\) of the RHS was considered to be the square of \(+2\) at Step 4), I would have first gotten the equation’s other solution (which is \(7\)). al-Khwārizmī did give this other solution as well, at Step 6, but no adjustment involving negative quantities is needed in the algebra tile representation at that step.
Example 8a: Squares and Numbers are Equal to Roots (Type 5), modeling via subtraction

In the second modeling alternative for this same equation (shown below as Example 8b), the transfer of the 10 roots that takes place at Step 3 is modeled using negative algebra tiles (“\(-x\)”), rather than the subtraction symbol. Examples 8a and 8b could be taught via a comparative approach to students, in particular those who are prospective teachers, so that they are led to reflect on the advantages and disadvantages of the two approaches. For instance, whereas Example 8a emphasizes the use of the subtraction operation applied to positive quantities, Example 8b seems to emphasize the use of the addition operation applied to negative quantities. This in turn could lead to the discussion of other topics, such as the concept of an additive inverse and its relevance to subtraction.
Example 8b: Squares and Numbers are Equal to Roots (Type 5), modeling via “-x” tiles
Given the complicated nature of the modeling procedure for equation type 5, it could be helpful to offer students a second example to work out. Example 9 thus shows al-Khwārizmī’s second example for this case [Rosen 1831, 56], following the subtraction approach used in Example 8a. This particular example suggests yet another interesting question for class discussion: why did al-Khwarizmi only give one solution (\(x=2\)) to this equation, and not even mention the second solution (\(x= 10\))?
Example 9: Squares and Numbers are Equal to Roots (Type 5)
Notes
3. Type 5 was also the most complicated case for al-Khwarizmi, as suggested by the comments about the special nature of this case in the following excerpt from his treatise [Rosen 1831, 11–12]:
When you meet with an instance which refers you to this case [squares + numbers = roots], try its solution by addition, and if that do not serve, then subtraction certainly will.
For in this case both addition and subtraction may be employed, which will not answer in any other of the three cases in which the number of the roots must be halved.
And know, that, when in a question belonging to this case you have halved the number of the roots and multiplied the moiety by itself, if the product be less than the number of dirhems connected with the square, then the instance is impossible; but if the product be equal to the dirhems by themselves, then the root of the square is equal to the moiety of the roots alone, without either addition or subtraction.
Instructors who wish to extend this exploration could have their students explore what exactly al-Khwarizmi meant here. However, since deciphering his meaning seems like it would be best carried out symbolically rather than with algebra tiles, such an exploration would be tangential to the main thrust of the activity presented in this article.
Algebra Tiles Explorations of al-Khwārizmī ’s Equation Types: Roots and Numbers are Equal to Squares
al-Khwārizmī’s sixth and final type of equation can again be modeled using either subtraction or "\(-x\)" tiles; we show only the former alternative. Because the Type 6 equation that was worked out by al-Khwārizmī (“three roots and four of simple numbers are equal to a square”) involves fractions and mixed numbers—which cannot be modeled using algebra tiles—we present a slightly-modified example in its place, following the procedure given in [Rosen 1831, 12]. We also show only the procedure for producing the positive root, as the modification for producing the negative root is analogous to how we proceeded in Example 7.
Example 10: Roots and Numbers are Equal to Squares (Type 6)