Kepler and the Rhombic Dodecahedron: Building a Rhombic Dodecahedron

To enjoy this polyhedron, to learn more about it, and to convince ourselves of its beautiful properties, it is highly recommended that readers make an actual rhombic dodecahedron themselves.

Figure 12 provides a template (or net) that can used to build a small paperboard box in the beautiful shape of a rhombic dodecahedron. This template—and a variant of it which produces a box with the shape of a bee cell (Figure 13)—were designed by John Jeremiah Edminster.

Figure 10. Two completed paperboard models: a bee cell and a rhombic dodecahedron.
Design by John Jeremiah Edminster.

Figure 11. View of the two models as small boxes with open tops.
Design by John Jeremiah Edminster.

To build a model of a rhombic dodecahedron, simply download, print, cut out, and glue together the net shown in Figure 12. (Be sure to cut out all of the triangles, since only the rhombi become faces of the polyhedron.) Looking at this template, we see a horizontal row of six rhombi, the two ends of which should be glued together to make a belt with three rhombi above it and three rhombi below it. To close the polyhedron, bring each set of three rhombi (top and bottom) together with the rounded “tabs” tucked inside.

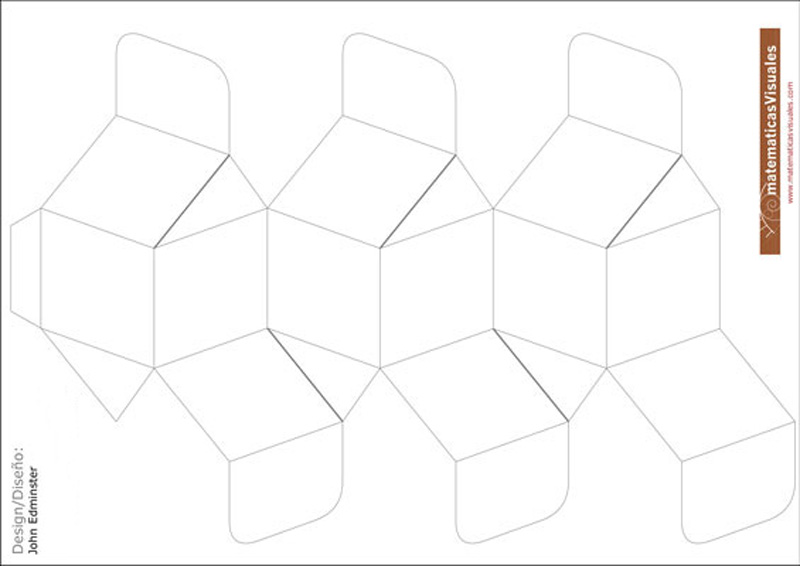
Figure 12. Net of a rhombic dodecahedron. Used by permission
of the designer, John Jeremiah Edminster.

Figure 13 gives a template for the net of a box that is a model of a bee cell. Again, be sure to cut out all the triangles; the polygons in the bottom row of the template (which become the flat top of the box) also need to be cut along their shared edges so that they can be folded separately.

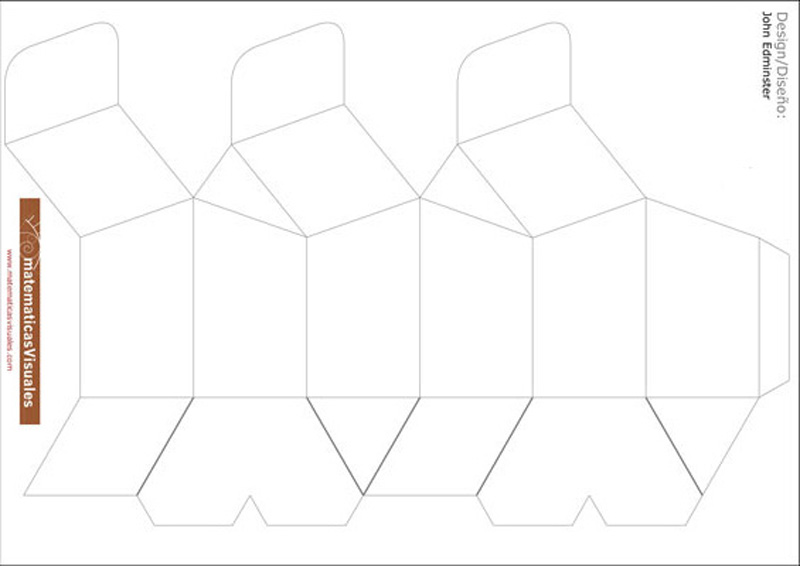
Figure 13. Net of a bee cell. Used by permission of the designer, John Jeremiah Edminster.

If we build several of these polyhedra, we can explore how bees make their honeycombs, as well as investigate the space-tessellation property of the rhombic dodecahedron described in the previous section of this article.

Years after I started building these models with students, it was a pleasure to come across an old article, written in 1936 by W. Hope-Jones in the best tradition in teaching. The title of this inspirational article is “The Rhombic Dodecahedron for the Young”; it is full of good ideas and written with enthusiasm:

This interesting solid has tended too much in the past to be classified as “for adults only” (and for not too many of them); but because it supplies the answer to a question which every intelligent youngster asks himself, I think it is worthwhile to try and smooth the path of any teacher who wants to let children of (say) 13 share in some of its treasures.

The bee's cell is very well worth doing for its own sake, in addition to its value as leading up to the rhombic dodecahedron. Designing it on the flat is our job; but cutting out a given design and gumming it up into its three-dimensional shape is excellent fun for children [Hope-Jones 1936, 254].