An Ancient Egyptian Mathematical Photo Album – Hieroglyph Numerals and More
The Egyptian hieroglyph numeration system is studied in many mathematics courses for pre-service elementary education students as well as in history of mathematics courses. Starting with the 2009 MAA Study Tour to Egypt, the author began collecting photographs of authentic hieroglyphs to show students during presentations on numeration systems and ancient Egyptian mathematics. Students are fascinated to see the actual hieroglyphs, rather than just drawings or typeset characters. The purpose of this article is to share some of these images, so that others may also use them in their classrooms. The article contains a sampling of photographs (taken by the author unless otherwise noted) that can be used (with attribution, CC BY 4.0) in classrooms to illustrate the genuine use of hieroglyphic numerals in ancient Egypt. After a brief overview of Egyptian hieroglyphic numerals and their uses, the sections of this article are organized by location of the hieroglyphs. (Note: For more details on Egyptian mathematics and recent scholarly theories in Egyptology, see [Imhausen 2016].)
Hieroglyphs were used on temple walls, stelae, and early papyri in ancient Egypt. The term “hieroglyph” comes from Greek for “sacred carvings.” “Hieroglyph” is a noun and “hieroglyphic” is the corresponding adjective. As time passed, a cursive style of writing, called hieratic, was developed for writing on papyrus. In this article, we will focus on hieroglyphs. So, we will not be including images from the two classic sources on Egyptian mathematics, the Rhind Mathematical Papyrus or the Moscow Mathematical Papyrus, since both of these papyri are in hieratic script.
In classrooms, the Egyptian hieroglyph numeration system is often presented, possibly with other numeration systems, as a comparison to the base ten, place-value, Hindu-Arabic numeration system that we use today. The hieroglyphic system is also base ten, with special hieroglyphs for the powers of ten from 0 to 6 (ones to millions). However, it is not a place-value system. Instead, it is additive, like early Roman numerals, in which a specific numeric hieroglyph can be repeated from one to nine times. To write counting numbers, the symbols are written in decreasing order, with like symbols grouped together and sometimes stacked. Egyptian hieroglyphs may be written to be read from right to left, left to right, or top to bottom. To determine whether one reads from right to left or left to right, the rule is to read toward any faces in the hieroglyphs. Whenever the hieroglyphs are in columns, they are always read from top to bottom. In Figure 1, which is from the Edfu Temple, we can see six of the seven hieroglyphs that are used in creating natural numbers.

Figure 1. 1,333,330 in Egyptian hieroglyphs from the Edfu Temple (237–57 BCE) in Egypt.
All photos in this article—except for Figures 2–4, 15, and 40—were taken by the author
and can be used with attribution under a CC BY 4.0 license.
The hieroglyph on the left is the Egyptian god Heh (chaos or infinity), representing one million. Next, a tadpole hieroglyph represents 100,000. The bent finger hieroglyph is 10,000; the lotus flower is 1000; the coil of rope is 100; and the hobble (used for cattle and missing the crossbar) is 10. Reading from left to right, the hieroglyph number is 1,333,330. The one missing numeric hieroglyph symbol in the photo is the stroke or tally mark for 1.
An Ancient Egyptian Mathematical Photo Album: Early Hieroglyphs
The beginnings of mathematics and of writing are closely intertwined. It may even be that counting and keeping records of amounts led to the invention of writing. One place to view rare examples of early hieroglyphs is in the Egyptian Museum of Antiquities in Cairo. (The Grand Egyptian Museum, located in Giza, Egypt, is slated to open in 2022.) When the author visited Egypt on an MAA Study Tour in 2009, photographs were not allowed inside museums and certain other places, such as tombs in the Valley of the Kings. So, the images of early hieroglyphs below are from the internet.
The centralized government of Egypt, with the pharaoh at its head, had a need for counting numbers. Among other things, the bureaucracy kept track of supplies, soldiers, taxes owed, and taxes collected. Pictured in Figure 2 are inventory tags—claimed by some to contain the earliest hieroglyphs [Mattessich 2002, p. 196]. Notice the tally marks.

Figure 2. Very early hieroglyphs (ca 3700–3050 BCE) on inventory tags found in a tomb in Abydos. Retrieved from https://web.archive.org/web/20120415143131/http://www.dainst.org/en/project/abydos?ft=all.
Figure 3 displays another of the earliest examples of Egyptian hieroglyphs, the Narmer Palette, located in the Egyptian Museum of Antiquities in Cairo, Egypt. The palette tells the story of Narmer unifying Lower and Upper Egypt and dates to about 3100 BCE.

Figure 3. The Narmer Palette (ca 3200–3000 BCE) which contains early hieroglyphs. Egyptian Museum of Antiquities.
If we zoom in on the upper right corner of the side of the palette pictured on the right in Figure 3, we see a falcon, representing the pharaoh, above six papyrus plants, holding a person by a nose ring. The papyrus plant may be an early hieroglyph for 1000, which then evolved into the lotus plant hieroglyph. So this portion of the palette may be stating that Narmer took 6000 captives [Brier 2016].

Figure 4. 6000 in early hieroglyphs on the Narmer Palette. Detail from Figure 3.
An Ancient Egyptian Mathematical Photo Album: Counting Numbers
Counting numbers were a crucial part of the centralized government of ancient Egypt, since the bureaucracy needed to keep records of many things, including inventories, workers, time, and taxes. As mentioned above, the Egyptians used an additive decimal system with symbols for the powers of ten from 0 to 6, in which like symbols were grouped together in descending order, and often stacked for aesthetics. If the writing was in columns, the hieroglyphs were to be read from top to bottom. If written horizontally, the hieroglyphs were meant to be read toward faces. So, they might be read left to right or right to left. Typically, the number followed the noun (usually singular) it was counting.

Figure 5: Numeric hieroglyphs in the Louvre (Annals of Thutmose III, 1479–1425 BCE, Karnak Temple).
The example in Figure 5 is from the Louvre and has the writing in columns. Notice the calf at the top of the picture is facing to the right. Thus, the hieroglyphs are read from top to bottom and, within each line, from right to left. The number pictured is composed of four lotus flowers (4000), six stacked coils of rope (600), two hobbles (20), and two tally marks (2), namely 4622. Since the number follows “calf,” it translates as 4622 calves.
The next example is from a papyrus in the Egyptian museum in Turin, Italy, and it also has the writing in columns. From the picture on the left, we see that the person and bird figures face right. So, although the direction does not actually matter in this particular example, the hieroglyphs on each line are read right to left. With four coils of rope (400), five hobbles (50), and three tally marks (3), the number is 453.


Figure 6. Hieroglyphs, read top to bottom and right to left on each line, on a papyrus (1076–722 BCE) in Turin, Italy.
The image on the right shows a close-up of the number 453.
The final examples of counting numbers in this section are from the Karnak Temple (begun around 2000 BCE with expansions through about 30 BCE) in Luxor, Egypt. These hieroglyphs appear on the same wall, one not far above the other. They are read top to bottom and right to left within each row. The number pictured on the left in Figure 7 is 4820, written with four lotus flowers (4000), eight coils of rope (800), and two hobbles (20). The image on the right displays 6823.


Figure 7. Counting numbers on a wall in the Karnak Temple (ca 2000–30 BCE) of Luxor, Egypt.
The image on the left shows 4820 while the image on the right shows 6823.
An Ancient Egyptian Mathematical Photo Album: Fractions
Fractions in ancient Egypt were almost exclusively unit fractions. According to Annette Imhausen [2016, p. 52], “The Egyptian concept of fractions, that is, parts of a whole, was fundamentally different from our modern understanding.” The notation that was used to signify a fraction—a mouth hieroglyph representing “part”—corresponds with this viewpoint and the use of unit fractions. The rare exceptions to unit fractions include special symbols for \(\frac{1}{2}\), \(\frac{2}{3}\), \(\frac{1}{4}\), and \(\frac{3}{4}\).
The pictures below demonstrate the unit fractions \(\frac{1}{6}\), \(\frac{1}{16}\), and \(\frac{1}{120}\), respectively.



Figure 8. Fractions on temple walls: \(\frac{1}{6}\) (Edfu, 237–57 BCE), \(\frac{1}{16}\) (Kom Ombu, 180–47 BCE),
\(\frac{1}{120}\) (Kom Ombu, 180–47 BCE).
Figure 9. Fractions on a cubit rod (1327–1295 BCE) in the Louvre.
Notice the special hieroglyph for \(\frac{1}{2}\) on the far right.
A fraction such as \(\frac{13}{16}\), which is not a unit fraction, would be written as a sequence of unit fractions written in decreasing order of denominators, which, when added together, would sum to \(\frac{13}{16}\), such as \(\frac{1}{2}\) \(\frac{1}{4}\) \(\frac{1}{16}\). Figure 10 gives an example to show that expressing non-unit fractions in this way is not unique. The special symbol for \(\frac{1}{2}\) is in the image on the left in Figure 10, followed by \(\frac{1}{3}\) to represent the summed fraction \(\frac{5}{6}\). In the image on the right in Figure 10, the special symbol for \(\frac{2}{3}\) (Ptolemaic version) is followed by \(\frac{1}{6}\) to form another representation of \(\frac{5}{6}\).


Figure 10. Non-unit fractions on a wall in the Edfu Temple (237–57 BCE).
Notice the special hieroglyph for \(\frac{1}{2}\) in the left image and \(\frac{2}{3}\) in the right image.
Thus, the image on the left represents \(\frac{1}{2} + \frac{1}{3} = \frac{5}{6}\), while the image on the right also represents \(\frac{5}{6}\), but as \(\frac{2}{3} + \frac{1}{6}\).
An Ancient Egyptian Mathematical Photo Album: Calendars
Egyptian hieroglyph numerals were also used in recording time. The Egyptian annual calendar consisted of five extra days and twelve months (with each month having three weeks and each week containing ten days) for a total of 365 days. The year was also broken down into three seasons of four months each: inundation called Akhet (when the Nile annually flooded depositing fertile top soil, June to September); emergence or growing season called Peret (October to February); and harvest season called Shemu (March to May) [Brier 2016].
Figure 11 is from a calendar at the Kom Ombo Temple. The circle on the right of each panel is the sun disk determinative to indicate that the writing presents a date. From the top, we see 27, 28, 29 (the circle with the line across represents 9), the 30th day of the last month of the harvest season, the first day of the first month of inundation, 2, 3, and so on.
The Egyptians did not keep a running count of the years. As each new pharaoh began his or her reign, the year count would reset. So, a particular date would be given as the year of the reign of the current pharaoh, the month of the season, and the day.

Figure 11. Portion of a calendar showing hieroglyph numerals from the Kom Ombo Temple (180–47 BCE).
An Ancient Egyptian Mathematical Photo Album: Caveats
The Egyptian hieroglyphic script consists of over 1000 characters representing either a phonetic sound, an ideogram for a specific concept, or a determinative at the end of a word to clarify its meaning. Not surprisingly, there are some challenges to reading hieroglyphs. For example, there is no punctuation to separate sentences or clauses, although comprehension is aided by knowing that verbs occur at the beginnings of sentences. Although determinatives follow some words, there are nonetheless cases where it is difficult to tell when one word ends and the next begins. Variations can occur among the symbols, since they were created by various scribes or carvers over four millennia. Also, there are places where the hieroglyphs have been damaged. In addition, there are symbols which have different meanings depending on the context. We will discuss several such hieroglyphs related to mathematical notation.
First, the mouth symbol that is used to denote a unit fraction has several other meanings. It is part of the hieroglyphic alphabet representing the letter “R”, and it is also used as a stand-alone word meaning “to” a place (there is another word for “to” a person) or “by”. Later, in Figure 14, the mouth symbol is used both to denote a unit fraction and as “by”.
Also in Figure 14, we see a hieroglyph that looks like the side of a statue base used to mean “at” or “from” or “side”, while a smaller version represents \(\frac{1}{2}\). (Compare with Figure 38.)
The coiled rope symbol representing 100 is also used as a replacement for the quail chick hieroglyph representing the letter “W” or the sound “oo”.
While the stroke can represent the number one, it appears much more often as a determinative following a hieroglyph to indicate it is being used as an ideogram, i.e., a face hieroglyph followed by a stroke means either “face” or something related to a face. The determinative stroke is typically shorter than the stroke for the number 1, as can be seen in Figure 12.

Figure 12. Example of a stroke used as a determinative (twice on the left)
and as a numeral (7 on the right) on a wall in the Edfu Temple (237–57 BCE).
The number in Figure 13 could easily be mistakenly read as 1,333,331, instead of correctly as 1,333,330. Upon closer examination, one sees the stroke is not part of the numeral but is actually an ideogram determinative following the heart hieroglyph.

Figure 13. Example of a stroke used as a determinative and not a numeral on a wall in the Edfu Temple (237–57 BCE).
Three strokes also commonly occur in hieroglyphic text to denote that the preceding word is a plural. Figure 18 shows an example of three strokes indicating a word is plural. Two slanted strokes are also used to denote a noun is plural, specifically in the case of two objects.
An Ancient Egyptian Mathematical Photo Album: Samples of Numeral Hieroglyphs by Location
Most people would expect to find Egyptian hieroglyphs in ancient temple ruins in Egypt. However, Egyptian hieroglyphs can also be found in museums around the world. Many world history and art museums have Egyptian collections, in which hieroglyphs can be found on pieces of walls, sarcophagi, stelae, vessels, papyri, statues, jewelry, and other objects. In fact, one way to apply this article with students is to explore those collections during in-person or virtual field trips.
The following pages highlight artifacts marked with hieroglyphic numerals that are held in five locations visited by the author:


- British Museum
- Rosetta Stone
- Rhind Mathematical Papyrus
- Stela of Merymose’s Campaign Against the Nubians
- Louvre
- Annals of Thutmose III
- Cubit Rod
- Sculptures of Scribes and Examples of Scribal Tools
- Museo Egizio in Turin, Italy
- Cubit Rods
- Amduat Papyrus

Images of each location retrieved from Wikimedia Commons.
An Ancient Egyptian Mathematical Photo Album: Samples of Numeral Hieroglyphs by Location – Edfu Temple
The Edfu Temple (237–57 BCE), a Ptolemaic temple dedicated to Horus and made of sandstone, is considered one of the best preserved ancient Egyptian temples [Wilkinson 2017]. French Egyptologist Émile Chassinet spent 40 years copying the hieroglyphs from the reliefs and walls, in order to preserve the eroding markings. More recently, the Edfu Project was begun by Dieter Kurth in 1986 and sponsored by the Göttingen Academy of Sciences from 2002 to 2017, with the goal of translating the Edfu texts. Eight large volumes of German translations along with transliterations of the hieroglyphs were published. The Edfu Database contains German translations, photographs, and clips from Chassinet’s work for portions of the Edfu Temple. An area known as the Cadastral text has a plethora of fractions, but the photographs are not available online at this time.
According to François Gaudard [2010, p. 173], Ptolemaic hieroglyphs, like those in the Edfu Temple, can be challenging to translate, even for Egyptologists. The number of hieroglyphic symbols in the Middle Kingdom (sources vary on its dating but converge around roughly 2040 to 1782 BCE) was about 760 while the number grew to several thousand signs during the Ptolemaic period (after Alexander the Great until roughly 200 CE). Gaudard mentions that a head hieroglyph represented the number seven “simply because the head has seven openings, namely, two eyes, two ears, two nostrils, and a mouth.” We conjecture that the 5-pointed star hieroglyph in Figure 14 is used for five. So, the middle portion of text could be read (left to right) as “at 37 \(\frac{1}{2}\) \(\frac{1}{3}\) by 25 \(\frac{2}{3}\) \(\frac{1}{6}\).” The hieroglyph in the bottom right corner is a determinative for "building” or “house.”

Figure 14. Fractions on a wall of the Edfu Temple (237–57 BCE).
The 5-pointed star symbol as a representation for five seems to be confirmed by translations found in the Edfu Database. One example is a portion of text translated as “A large decorated gate is between them, at 26 \(\frac{2}{3}\) by 10 (cubits). Its perfect height of 40 cubits extends from its head to the soles of its feet.” The hieroglyphs corresponding to “at 26 \(\frac{2}{3}\) by 10 (cubits). Its perfect height of 40” can be seen in the two images (read right to left) in Figure 15.


Figure 15. Reading from right to left “at 26 \(\frac{2}{3}\) by 10 (cubits). Its perfect height of 40.”
Images 3922 and 3921 retrieved from the Edfu Database (Edfu Temple, 237–57 BCE).
Images have been cropped to show the relevant hieroglyphs.
Below are a few more photographs from the Edfu Temple. The first one, which is read from top to bottom and from right to left within each row, contains a four and a seven. It demonstrates how the Egyptians were concerned with aesthetics. Notice how the four strokes fit well in a single line while the seven is stacked in rows of four and three, respectively, and shares a row with another hieroglyph and a determinative stroke.

Figure 16. The numerals 4 and 7 on a wall in the Edfu Temple (237–57 BCE).

Figure 17. Close-up of 1,000,000 and 100,000 and 10,000 in the Edfu Temple (237–57 BCE).

Figure 18. Two hundred on a wall in the Edfu Temple (237–57 BCE).
The three strokes indicate a plural noun since they appear underneath another hieroglyph.
Continue to Kom Ombo Temple page.
Return to list of Locations.
An Ancient Egyptian Mathematical Photo Album: Samples of Numeral Hieroglyphs by Location – Kom Ombo Temple
The Kom Ombo Temple (180–47 BCE), located north of Aswan along the Nile River, is known for a scene depicting what may be medical instruments. However, of interest to mathematicians is another part of the scene that contains a list of city names and fractions.

Figure 19. Scene from a wall of the Kom Ombu Temple (180–47 BCE).
The middle section contains what appears to be medical instruments,
while the right side shows a list of city names and fractions.

Figure 20. A closer view of the scene in Figure 19 containing what are believed to be
medical instruments on the left and a list of city names and fractions in the middle of the photo.
This middle section is read from right to left, with each line containing a fraction followed by a city name.
The hieroglyph of a circle with an x in the middle, at the end of each line, is the determinative for town.
Zooming in on the list of fractions, one sees the special hieroglyph used for \(\frac{1}{2}\) in the first row of the photo. According to Coppens & Vymazalová [2010, p. 129], this list of fractions and cities has been placed in a vase above a basin and signifies a recipe for bringing restoration to Egypt.

Figure 21. Close-up of a scene from a wall of the Kom Ombu Temple (180–47 BCE) showing a list of city names and fractions.
Many of the temples in Egypt had nilometers, which the priests used to measure the height of the Nile inundation each year. Taxes were then determined based on the water level. If the floodwaters were high, taxes were higher, since it was expected that fields would receive a good amount of new topsoil, resulting in a plentiful harvest. If the floodwaters were low, then taxes would be correspondingly lower, since the harvest yields were expected to be lower. The photo below shows the nilometer at the Kom Ombo Temple.

Figure 22. Nilometer at the Kom Ombo Temple (180–47 BCE) in Egypt.
In the section on the Egyptian Calendar earlier in this article, Figure 11 was a photo from the Kom Ombo Temple. Figure 23, the last image in the Kom Ombo section of our photo album, is a wider view of the portion of the wall with the calendar, which shows dates (using hieroglyphic numerals) and the corresponding events at the temple for each date.

Figure 23. Calendar at the Kom Ombo Temple (180–47 BCE) in Egypt.
Continue to British Museum page.
Return to list of Locations.
An Ancient Egyptian Mathematical Photo Album: Samples of Numeral Hieroglyphs by Location – British Museum
The British Museum is home to two very important objects dealing with ancient Egypt—the Rosetta Stone and the Rhind Mathematical Papyrus. We will discuss each of these briefly, before showing photos of other hieroglyph numerals in the museum from the stela of Merymose.
Rosetta Stone
The Rosetta Stone was an important key to unlocking the decipherment of ancient Egyptian hieroglyphs. It was discovered during Napoleon’s 1798–1801 expedition to Egypt. The stela had an inscription given in three scripts: hieroglyphic, demotic, and Greek. With the defeat of the French by the British in the military campaign in Egypt, the Rosetta Stone became a spoil of war and was placed in the British Museum. The text is a royal decree and contains a few dates, however much of the hieroglyphic script of the royal decree is missing. The British Museum also has a replica which can be touched and is easier to search for numerals.
Figure 24. The Rosetta Stone (196 BCE) on display in the British Museum in London.

Figure 25. (Top) A close-up of the hieroglyphic script on the Rosetta Stone (196 BCE).
(Bottom) The touchable replica in the British Museum.
Rhind Mathematical Papyrus
There are many papyri at the British Museum which were acquired from the collection of the Scotsman Alexander Henry Rhind (1833–1863). The one labeled as the Rhind Mathematical Papyrus (1650 BCE) is one of the major sources of knowledge of Egyptian mathematics. Although the writing is hieratic and not hieroglyphic, we would be remiss not to mention this important artifact. The Rhind Mathematical Papyrus is not currently on display at the British Museum, but one can request permission in advance to view it. (The British Museum study rooms were closed during the COVID-19 pandemic.) More information can be found on the website of the British Museum. One can also view several images of each side of the Rhind Mathematical Papyrus (Objects EA10057 and EA10058) in the British Museum Collections. The author was not allowed to take her camera into the locked storage room when she viewed the Rhind Mathematical Papyrus in 2018.
The Stela of Merymose’s Campaign Against the Nubians
The British Museum has an extensive Egyptian collection, and one can hunt for hieroglyph numerals on the various sarcophagi, stelae, and statues. A stela that is abounding in hieroglyph numerals is the one that outlines the campaign of Merymose against the Nubians during the reign of Amenhotep III in the 18th Dynasty . Figure 26 shows the entire stela. The photos in Figure 27 display a sample of the numerals which appear.

Figure 26. The Merymose stela (ca 1380 BCE) in the British Museum.



Figure 27. Close-ups of the Merymose stela (ca 1380 BCE, British Museum) showing hieroglyph numerals.
An Ancient Egyptian Mathematical Photo Album: Samples of Numeral Hieroglyphs by Location – The Louvre
The Louvre, the most well-known art museum in the world, houses one of the largest collections of ancient Egyptian artifacts and art. Hieroglyphs appear on several of the objects, and by looking carefully one can find Egyptian numerals. In this section we present a photo album of hieroglyphic numerals from the Annals of Thutmose III, a cubit rod showing fractions, and art and instruments of Egyptian scribes, who would have been transcribing and working with the numbers.
Annals of Thutmose III
The first group of photos from the Louvre show the Annals of Thutmose III on a sandstone wall that was originally in Karnak in Egypt. The first four pictures show larger sections of the wall. These are followed by a selection of photos of specific numerals found on the wall to demonstrate various ways the digits of the numerals are aligned. More numerals can be found by zooming in on the first four photos.
Figure 28. Part of the left side of the Annals of Thutmose III (1479–1425 BCE, Karnak Temple) in the Louvre.

Figure 29. More of the left side of the Annals of Thutmose III (1479–1425 BCE, Karnak Temple) in the Louvre.
Figure 30. The middle portion of the Annals of Thutmose III (1479–1425 BCE, Karnak Temple) in the Louvre.
Figure 31. The right side of the Annals of Thutmose III (1479–1425 BCE, Karnak Temple) in the Louvre.


Figure 32. 4,622 and possibly 5,428 (damaged) in Egyptian hieroglyphs
from Annals of Thutmose III (1479–1425 BCE, Karnak Temple) in the Louvre.


Figure 33. Possibly 329 (damaged) and 470 in Egyptian hieroglyphs
from Annals of Thutmose III (1479–1425 BCE, Karnak Temple) in the Louvre.


Figure 34. 276 and 618 in Egyptian hieroglyphs
from Annals of Thutmose III (1479–1425 BCE, Karnak Temple) in the Louvre.

Figure 35. 1200 in Egyptian hieroglyphs
from Annals of Thutmose III (1479–1425 BCE, Karnak Temple) in the Louvre.
Cubit Rod
A fascinating mathematical object in the Egyptian collection in the Louvre is a cubit rod that was found in the tomb of Maya in Saqqara. Maya was an important official who held several positions, including the Minister of Finance, for the pharaoh Tutankhamun.

Figure 36. The cubit rod (1327–1295 BCE) of Maya in the Louvre.
A cubit, the length from the elbow to the tip of the middle finger, was the basic unit of measure in ancient Egypt. A cubit was divided into seven palms and each palm was divided into four fingers. The finger hieroglyph (which is also used to represent 10,000) is used to represent the length, 1 finger. If we look at the far left of the above cubit (see Figure 37), in the middle row, we see 1 finger, 2 fingers, and 3 fingers marked off. Continuing on in the middle row, we have a palm, 1 palm and 1 finger, 1 palm and 2 fingers, etc. The middle row (and the top row with other hieroglyphs) is partitioned into a total of 28 fingers.

Figure 37. The left end of the cubit rod (1327–1295 BCE) of Maya in the Louvre.
The right end of the cubit has fingers marked into parts from one-half up to sixteenths. Above the markings are the labels in Egyptian fractions, starting with the special hieroglyph for \(\frac{1}{2}\) and then using the mouth symbol to denote fraction for \(\frac{1}{3}\) to \(\frac{1}{16}\). Figure 38 shows a close-up of the right end with the markings from \(\frac{1}{2}\) to \(\frac{1}{14}\).

Figure 38. The right end of the cubit rod (1327–1295 BCE) of Maya in the Louvre.
Scribes and Scribal Tools
Egyptian scribes, some of the few literate people in ancient Egypt, were responsible for keeping records and accounts, writing letters, and recording events. According to The Teaching of Khety, an ancient Egyptian text of a father’s advice to his son, the vocation of scribe was a desirable one and “there is no job without a boss except for the scribe” [Wilkinson 2017, pp. 289–299]. Khety explained that being a scribe had advantages over other professions, such as not smelling like the smith (“who stinks more than fish roe”) and the stoker (“his fingers are putrid and smell of corpses”); not having to watch out for crocodiles like the fisherman and washerman (who also “handles the clothes of menstruating women”); not having to be out in the weather like the reed cutter, arrow maker, and messenger; and not having to do back-breaking work like the gardener, mason, and farmer. Photos of several examples of scribes at work and scribal tools are given below.


Figure 39. Representations of various scribes and their tools in the Louvre collections.
Continue to Turin’s Museo Egizio page.
Return to list of Locations.
An Ancient Egyptian Mathematical Photo Album: Samples of Numeral Hieroglyphs by Location – Turin’s Museo Egizio
Turin, Italy may not seem like an obvious place to search for Egyptian numeric hieroglyphs, but it is home to the Museo Egizio, billed as the “world’s oldest museum devoted entirely to ancient Egyptian culture.” The author visited this museum during the 2012 MAA study tour to Italy. Below are pictures from that trip which feature Egyptian numerals. Additionally, a database, including photographs, of over 250 papyri (most in hieratic script) housed at the museum is available (requires registration).
The museum has four cubit rods, two of which were found in the tomb of Kha, a royal architect. One of these folds in half, making it more portable for practical use. The other is covered in gold-leaf and was given to Kha in appreciation by the pharaoh Amenhotep II. The two images in Figure 40 show this commemorative cubit; first, one side covered by hieroglyphs and second, a portion of a side with the finger measurement broken into parts from \(\frac{1}{2}\) to \(\frac{1}{16}\), similar to the cubit from the Louvre, pictured in Figures 36–38.


Figure 40. An 18th Dynasty gold-leaf cubit from the tomb of Kha, now in the Museo Egizio in Turin.
Second image has been cropped to focus on the fractions. Retrieved from Museo Egizio Online Collection
(Inv. No. S_8647) and used under the Creative Commons 2.0 Italy license.
Figure 41 shows 453 in hieroglyphs in an Amduat papyrus (1076–722 BCE). Originally the Book of the Amduat was carved on royal tomb walls in the Valley of the Kings, but later it was written on papyri so that less-wealthy people could include it in their burial. The Amduat explains what happens to the sun during each of the 12 hours it passes through the underworld daily before being reborn at dawn.

Figure 41. The number 453 in hieroglyphs from the Amduat papyrus (1076–722 BCE) in the Museo Egizio in Turin, Italy.
Continue to the next section, JSesh Hieroglyph Program.
Return to list of Locations.
An Ancient Egyptian Mathematical Photo Album: JSesh Hieroglyph Program
Instructors may want to create assignments that involve hieroglyph numerals not available in photographs. Of course, one can draw hieroglyphs by hand as the Egyptian scribes did. However, there is an Egyptian hieroglyph word processor available, called JSesh (Sesh is the Egyptian word for scribe). JSesh can be freely downloaded. The hieroglyphs are organized using a system widely employed by Egyptologists and created by Sir Alan H. Gardiner (1879–1963), who wrote the classic middle Egyptian hieroglyph text Egyptian Grammar. The hieroglyphs are classified into 25 categories, such as: man and his occupations, mammals, birds, temple furniture and sacred emblems, and strokes, along with an unclassified section and three other sections—tall narrow signs, low narrow signs, and broad narrow signs. Unfortunately, there is not a section on numerals. The JSesh hieroglyphs can be copied into other programs such as Word or saved as image files. The table below contains a selection of mathematical hieroglyphs as jpg files that can be copied or saved as images on a hard drive to make it easier for readers to access them for classroom use.
|
Hieroglyph |
Meaning |
Gardiner Classification |
|
|
one |
Z1 |
|
|
ten |
V20 |
|
|
hundred |
V1 |
|
|
thousand |
M12 |
|
|
ten thousand |
D50 |
|
|
hundred thousand |
I8 |
|
|
million |
C11 |
|
|
fraction/part |
D21 |
|
|
\(\frac{2}{3}\) |
D22 |
|
|
\(\frac{3}{4}\) |
D23 |
|
|
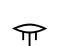
\(\frac{1}{2}\) |
Aa16 |
|
|
\(\frac{1}{4}\) |
Z9 |
|
|
cubit |
D42 |
|
|
palm |
D48 or D48a |
|
|
finger (measure) |
D50 |
An Ancient Egyptian Mathematical Photo Album: Using the Photos
As mentioned in the introduction, most of the photographs, except for those noted otherwise (specifically Figures 2–4, 15, and 40), were taken by the author. The author’s photographs can be freely downloaded for classroom use under a Creative Common Attribution 4.0 International license.
Instructors may wish to use the photographs in presentations to illustrate authentic Egyptian hieroglyphs. Seeing actual images of hieroglyphs can have a powerful impact on student learning. The author has observed how these photographs grab the interest of the students, bringing the mathematics to life and motivating students to learn more. The photos can also be used in assessments in which students are asked to determine the number being represented.
In addition to History of Mathematics courses, use of the photos would be appropriate in any class that includes the study of numeration systems, such as number theory or mathematics courses for pre-service teachers. Comparing and contrasting the Egyptian hieroglyph numerals with Hindu-Arabic numerals affords students the opportunity to think about place value and what it means to utilize a decimal (base ten) system. Since students have used the Hindu-Arabic numeration system for many years, it may be challenging for them to notice its properties. Seeing a decimal system that does not use place value may lead students to reflect on what it means to have a place-value system and on how using one affects arithmetical algorithms. The Egyptian numeration system could also be compared and contrasted with the Roman numeration system, which is still used today in some analog clocks, the release dates of movies, and the number of Super Bowl games.
The photographs can also be used to supplement activities involving Egyptian mathematics. David Reimer’s book, Count Like an Egyptian: A Hands-On Introduction to Ancient Mathematics [2014], is a good source for interesting problems for students. The author of this article has shown pictures of Egyptian fractions before students complete a group activity based on the “Fractions” chapter of Reimer’s book, especially pages 16–17. Students are divided into groups of two or three and given a paper plate, a plastic knife, and three slices of bread (each slice representing a loaf of bread). The students, assuming the role of work supervisors, are challenged to divide the three slices of bread among five workers in such a way that the workers receive obviously equal portions with at least some pieces of bread large enough to enjoy with honey. The latter condition is not met if a group wants to divide each slice of bread into five equal pieces, with each worker receiving three, as in the top row in Figure 42. This manner of thinking corresponds to a modern view of the fraction \(\frac{3}{5}\) as “three divided by five.” A solution which relates to how Egyptians may have viewed fractions as a sum of unit fractions is shown on the bottom row of Figure 42, where each worker would receive \(\frac{1}{2}\) and \(\frac{1}{5}\) of a \(\frac{1}{2}\), or \(\frac{1}{10}\).

Figure 42. A demonstration of two ways to “equally” divide three slices of bread among five people.
With the method in the top row, each person would receive three strips of bread.
With the method in the bottom row, each person would receive one half and one-tenth of a slice.
The author has also used some of the photographs, including those of scribes and scribal tools, in an “Egyptian Scribal School” activity with students at the secondary and undergraduate levels. The setting is a scribal school, with each student provided with a clipboard, paper, and fine point black marker to simulate a board, papyrus, and brush with ink. In addition to the photos of scribes and scribal tools, the students are shown some photos of hieroglyphs, including Figure 1, which shows six of the Egyptian numeric hieroglyphs, and Figure 6, a papyrus with hieroglyphs. (The author has a framed poster-size print of Figure 1, which she prominently displays in the classroom during the activity.) The students then practice writing each of the numeric hieroglyphs several times before solving arithmetic problems using Egyptian hieroglyphs and methods similar to those in Chapter 1 of Count Like an Egyptian [Reimer 2014].
An Ancient Egyptian Mathematical Photo Album: Conclusion
An introduction to ancient Egyptian mathematics, including the numeration system, benefits students. For example, by contrasting the Egyptian numeration system with the Hindu-Arabic system, pre-service teachers can gain a deeper understanding and appreciation of our decimal place-value system. Unit fractions are a great example of the importance of notation. The purpose of this article was to provide photographs of genuine Egyptian hieroglyphic numerals to motivate students and to make the historical use of numerals more real for them. Images were found in Egyptian temples and museums around the world. We hope that readers will be inspired to be on the hunt for Egyptian numerals themselves as they travel and visit museums with ancient Egyptian collections.
An Ancient Egyptian Mathematical Photo Album: References
Akademie der Wissenschaften zu Göttingen. 2022. Edfu Database. Accessed 1 August 2021. https://adw-goe.de/en/forschung/abgeschlossene-forschungsprojekte/akademienprogramm/edfu-projekt/die-datenbanken-des-edfu-projekts/edfu-datenbank/.
Brier, Bob. 2016. Decoding the Secrets of Egyptian Hieroglyphs. The Teaching Company.
Budge, E.A. Wallis. 1905. Translation of the Rosetta Stone. In The Nile, Notes for Travellers in Egypt, 199–211. 9th ed. London: Thos. Cook and Son.
Childers, Christopher, and Cynthia Huffman. 2015. Napoleon and Mathematics: A Case Study of the Interplay Between Mathematics and History. The Midwest Quarterly 56(3): 209–216.
Coppens, Filip, and Hana Vymazalová. 2010. Medicine, Mathematics and Magic Unite in a Scene from the Temple of Kom Ombo (KO 950). Anthropologie 48(2): 127–132.
Deutsches Archäologisches Institut. 2011. Abydos – Umm el-Qaab. Accessed 1 August 2021. https://web.archive.org/web/20120415143131/http://www.dainst.org/en/project/abydos?ft=all.
Gardiner, Alan H. 1973. Egyptian Grammar: Being an Introduction to the Study of Hieroglyphs. 7th ed. Oxford: Griffith Institute.
Gaudard, François. 2010. Ptolemaic Hieroglyphs. In Visible Language: Inventions of Writing in the Ancient Middle East and Beyond, edited by Christopher Woods, with Emily Teeter and Geoff Emberling, 173–175. Oriental Institute Museum Publications No. 32. Chicago: The Oriental Institute.
Imhausen, Annette. 2016. Mathematics in Ancient Egypt: A Contextual History. Princeton: Princeton University Press.
Louvre. n.d. Accessed 1 August 2021. https://www.louvre.fr/en.
Mattessich, Richard. 2002. The Oldest Writings, and Inventory Tags of Egypt. The Accounting Historians Journal. 29(1): 195–208.
Ministry of Tourism and Antiquities. 2019. The Egyptian Museum. Accessed 1 August 2021. https://egymonuments.gov.eg/en/museums/egyptian-museum.
Museo Egizio, Torino. 2018. Accessed 1 Aug. 2021. https://www.museoegizio.it/en/.
Reimer, David. 2014. Count Like an Egyptian. Princeton: Princeton University Press.
Rosmorduc, Serge. 2014. JSesh Documentation. Last modified 13 January 2022. Accessed 26 July 2021. http://jseshdoc.qenherkhopeshef.org.
Trustees of the British Museum. 2022. The British Museum. Accessed 1 August 2021. https://www.britishmuseum.org/.
Wilkinson, Richard H. 2000. The Complete Temples of Ancient Egypt. London: Thames & Hudson.
Wilkinson, Toby, trans. and intro. 2017. Writings from Ancient Egypt. London: Penguin Group USA.
An Ancient Egyptian Mathematical Photo Album: Acknowledgements and About the Author
Acknowledgements
The author is indebted to the editors and anonymous referees for help in improving the article. Many of the author’s photos in this article were taken on MAA study tours. Special thanks to Lisa Kolbe for initiating the MAA Study Tour program, along with Victor Katz and the planning committee. Additional thanks to mathematics professor and Egyptologist Jim Ritter for sharing his knowledge and expertise during the MAA tour to Egypt, and to all those who participated in the wonderful educational study trip experiences from 2003 to 2013. The author cherishes the special friendships formed while sharing the thrill of viewing objects and sites of mathematical importance in person.
About the Author
 |
Cynthia J. Huffman is a University Professor in the Department of Mathematics at Pittsburg State University. She has always been interested in history of mathematics but her interest was especially sparked by participation in several of the MAA Study Tours, beginning with one to Egypt in 2009. Her research areas include computational commutative algebra and history of mathematics. Dr. Huffman is a handbell soloist and has a black belt in Chinese Kenpo karate. |










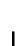
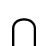
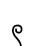






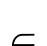

 or
or