A Selection of Problems from A.A. Markov’s Calculus of Probabilities: Problem 1 – Selecting Balls from a Vessel
This problem is very elementary and can be found in nearly every modern probability textbook, where it might be phrased as “selection without replacement.” It is a standard hypergeometric distribution example.
|
Задача 1ая. Из сосуда, содержащего \(a\) белых и \(b\) чёрных шаров и никаких других, вынимают одновременно или последовательно \(\alpha+\beta\) шаров, при чем, в случае последовательного вынимания, ни один из вынутых шаров не возвращают обратно в сосуд и новых туда также не подкладывают. Требуется определить вероятность, что между вынутыми таким образом шарами будеть \(\alpha\) белых и \(\beta\) чёрных. |
1st Problem. From a vessel containing \(a\) white and \(b\) black balls and no others, we select, simultaneously or consecutively, \(\alpha + \beta\) balls, for which, in the case of consecutive selection, none of the chosen balls are returned to the vessel and new ones are also not put back in.
It is required to determine the probability that there will be \( \alpha \) white and \(\beta \) black among the balls selected in this way.
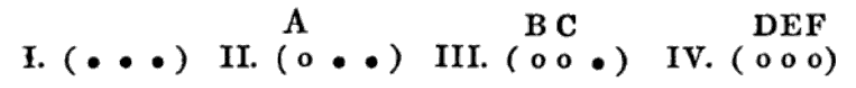
Figure 4. Augustus De Morgan’s illustration of a ball and vessel problem with three balls,
from page 53 of his 1838 Essay on Probabilities. Convergence Mathematical Treasures.
Continue to Markov's solution of Problem 1.
Skip to statement of Problem 2.
A Selection of Problems from A.A. Markov’s Calculus of Probabilities: Problem 1 – Solution
Review statement of Problem 1.
Solution: Assume that all the balls in the vessel are distinguished from one another by numbers in such a way that the white balls have numbers \(1, 2, 3, \dots, a\) and the black have numbers \(a+1, a+2, \dots, a+b\).
The numbers on the chosen balls must form some set of \(\alpha + \beta\) numbers from all \(a+b\) numbers \(1, 2, 3, \dots, a+b\).
The number of different sets of \(\alpha + \beta\) numbers that can be formed from \(a+b\) numbers is equal to \[\frac{(a+b)(a+b-1)(a+b-2)\cdots (a + b - \alpha - \beta +1)}{1\cdot 2 \cdot 3 \cdot\cdots \cdot (\alpha + \beta)}.\]
Corresponding to this, we can distinguish \[\frac{(a+b)(a+b-1)(a+b - 2) \cdots (a+b - \alpha - \beta +1)}{1\cdot 2 \cdot 3 \cdot\cdots \cdot (\alpha + \beta)}\] equally likely cases, each of which consists of the appearance of a specific \(\alpha + \beta\) numbers.
From all these exhaustive and disjoint cases, the appearance of \(\alpha\) white and \(\beta\) black balls is favored only for those in which any set of \(\alpha\) numbers from the group \(1, 2, 3,\dots, a\), together with any \(\beta\) numbers from the group \(a+1, a+2, \dots, a+b\), appear.
The number of distinct sets of \(\alpha\) numbers that can be formed from \(a\) numbers is equal to \(\frac{a(a-1) \cdots (a- \alpha + 1)}{1\cdot 2\cdot\cdots \cdot \alpha}\) and the number of distinct sets of \(\beta\) numbers that can be formed from \(b\) numbers is equal to \(\frac{b(b-1) \cdots (b- \beta + 1)}{1\cdot 2\cdot\cdots \cdot \beta}\).
Therefore, the number of distinct sets of \(\alpha + \beta\) numbers that can be formed from \(a+b\) numbers is expressed by the product \[ \frac{a(a-1) \cdots (a- \alpha + 1)}{1\cdot 2\cdot\cdots \cdot \alpha} \cdot \frac{b(b-1) \cdots (b- \beta + 1)}{1\cdot 2\cdot\cdots \cdot \beta}.\]
Then the number of cases considered that favor the appearance of \(\alpha\) white and \(\beta\) black balls is expressed by the indicated product.
And, consequently, the desired probability that among the chosen \(\alpha + \beta\) balls, there will be \(\alpha\) white and \(\beta\) black is expressed by the ratio \[\frac{\frac{a(a-1) \cdots (a- \alpha + 1)}{1\cdot 2\cdot\cdots \cdot \alpha} \cdot \frac{b(b-1) \cdots (b- \beta + 1)}{1\cdot 2\cdot\cdots \cdot \beta}} {\frac{(a+b)(a+b-1)(a+b-2)\cdots (a + b - \alpha - \beta +1)}{1\cdot 2 \cdot 3 \cdot\cdots \cdot (\alpha + \beta)}},\] which, after simple transformations, reduces to4 \[\frac{1\cdot 2 \cdot 3 \cdot\cdots \cdot (\alpha + \beta)}{1\cdot 2 \cdot\cdots \cdot \alpha \cdot 1\cdot 2 \cdot\cdots \cdot \beta} \cdot \frac{a(a-1) \cdots(a- \alpha + 1) \cdot b(b-1) \cdots (b- \beta + 1)}{(a+b)(a+b - 1)(a+b - 2) \cdots (a + b - \alpha - \beta +1)}.\]
Continue to Markov's presentation of a numerical example for Problem 1.
Skip to statement of Problem 2.
[4] In more compact notation, the solution reduces to: \(\frac{\binom{a}{\alpha} \binom{b}{\beta}}{\binom{a+b}{\alpha+\beta}}\).
A Selection of Problems from A.A. Markov’s Calculus of Probabilities: Problem 1 – Numerical Example
Review statement of Problem 1.
\(a=3,\ b=4,\ \alpha =2,\ \beta= 2 \).
Let us assume the white balls are set by the numbers 1, 2, 3 and the black by the numbers 4, 5, 6, 7.
The numbers on the chosen four balls can be represented by any of the following \(\frac{7 \cdot 6 \cdot 5 \cdot 4}{1\cdot 2 \cdot 3 \cdot4} = 35 \) sets:
| 1, 2, 3, 4 | 1, 2, 3, 5 | 1, 2, 3, 6 | 1, 2, 3, 7 | 1, 2, 4, 5 | 1, 2, 4, 6 | 1, 2, 4, 7 |
| 1, 2, 5, 6 | 1, 2, 5, 7 | 1, 2, 6, 7 | 1, 3, 4, 5 | 1, 3, 4, 6 | 1, 3, 4, 7 | 1, 3, 5, 6 |
| 1, 3, 5, 7 | 1, 3, 6, 7 | 1, 4, 5, 6 | 1, 4, 5, 7 | 1, 4, 6, 7 | 1, 5, 6, 7 | 2, 3, 4, 5 |
| 2, 3, 4, 6 | 2, 3, 4, 7 | 2, 3, 5, 6 | 2, 3, 5, 7 | 2, 3, 6, 7 | 2, 4, 5, 6 | 2, 4, 5, 7 |
| 2, 4, 6, 7 | 2, 5, 6, 7 | 3, 4, 5, 6 | 3, 4, 5, 7 | 3, 4, 6, 7 | 3, 5, 6, 7 | 4, 5, 6, 7 |
If two white and two black balls are chosen, then their numbers form one of the following \(\frac{3\cdot 2}{1\cdot2} \times \frac{4\cdot3}{1\cdot2} = 18\) sets:
| 1, 2, 4, 5 | 1, 2, 4, 6 | 1, 2, 4, 7 | 1, 2, 5, 6 | 1, 2, 5, 7 | 1, 2, 6, 7 |
| 1, 3, 4, 5 | 1, 3, 4, 6 | 1, 3, 4, 7 | 1, 3, 5, 6 | 1, 3, 5, 7 | 1, 3, 6, 7 |
| 2, 3, 4, 5 | 2, 3, 4, 6 | 2, 3, 4, 7 | 2, 3, 5, 6 | 2, 3, 5, 7 | 2, 3, 6, 7 |
In this way, we have 35 equally likely cases, 18 of which favor the considered event; consequently, the desired probability that there will be two of each color among the four chosen balls is \(\frac{18}{35}\).5
Note that Markov did not use “\(!\)” for factorial or any combinatorial notation such as \(\binom{n}{k}\) or \(\,_n C_k\), although such symbols had been around since the early 19th century. There are many other places in the text where Markov's writing could be simplified if even more modern terminology, such as “sample space,” “normal distribution,” and “variance” had been invented.
Markov provided a second solution to this problem. It is rather convoluted and not much is gained by including it here. It can be found (together with another numerical example) in the complete translation (pp. 78–80).
[5] In other words, \( \frac{\binom{3}{2}\binom{4}{2}}{\binom{7}{4}} = \frac{18}{35} \).