Historical Activities for Calculus - Module 3: Optimization Problems Then and Now
Module 3: Optimization Problems Then and Now
Perhaps the most important application of the differential calculus is the solution of optimization problems, where one wants to find the value of a variable that maximizes or minimizes a certain quantity. In this module we look at the history of some of these problems and their solutions.
- Heron's “Shortest Distance” Problem
- Snell's Law and the Principle of Least Time
- L'Hôpital's Pulley Problem and the Principle of Least Potential Energy
- Regiomontanus' Hanging Picture Problem
- Galileo and the Brachistochrone Problem
References
Paul J. Nahin, When Least is Best: How Mathematicians Discovered Many Clever Ways to Make Things as Small (or as Large) as Possible, Princeton University Press, 2004.
V.M. Tikhomirov, Stories about Maxima and Minima; translated from the Russian by Abe Shenitzer, American Mathematical Society/Mathematical Association of America, 1990.
Historical Activities for Calculus - Module 3: Optimization - Heron's Shortest Distance Problem
Heron's "Shortest Distance" Problem
One of the first non-trivial optimization problems was solved by Heron of Alexandria, who lived about 10-75 C.E. Heron's “Shortest Distance” Problem is as follows:
Given two points \(A\) and \(B\) on one side of a straight line, to find the point \(C\) on the line such that \(|AC|+|CB|\) is as small as possible.
Thus in Figure 26, below, one possible point \(C\) is shown, as well as the length of the path \(A\) to \(C\) to \(B.\)

Figure 26. A possible path from \(A\) to \(B\)
Figure 27. Use this GeoGebra applet to explore the solution to Heron's problem. You can drag \(C\) to determine the approximate length of the shortest path attainable.
To solve this problem mathematically, Heron noticed that if \(B\) is reflected across the line, to say \(B^{\prime},\) then for any point \(C\) on the line, \(|CB|=|CB^{\prime}|,\) and hence minimizing \(|AC|+|CB|\) is equivalent to minimizing \(|AC|+|C B^{\prime}|.\) But clearly since the shortest path from \(A\) to \( B^{\prime}\) is a straight line, the point \(C\) that minimizes \(|AC|+|C B^{\prime}|\) should be the point of intersection of the line with the line segment \(AB^{\prime}.\) Any other path, such as \(A\) to \(C^{\prime}\) to \(B^{\prime},\) will clearly be longer.
Figure 28. Heron's solution of the “Shortest Distance” Problem
Note that \(m\angle 2=m\angle 3\) by construction, and \(m\angle1=m\angle 3\) since these are vertical angles. Therefore, \(m\angle 1=m\angle 2.\) This is the equal angle law of reflection. It was Euclid who, over three hundred years earlier, had noted the now well-known Reflection Law for light:
Equal Angle Law of Reflection (or Euclid's Law of Reflection). If a beam of light is sent toward a mirror, then the angle of incidence equals the angle of reflection.
Heron appears to have been the first to observe that the Reflection Law implies that light always takes the shortest path.
As a matter of fact, the mirror in the Equal Angle Law of Reflection need not be flat. We may replace the line in Heron's problem by any concave curve (a curve is concave if it lies entirely on one side of any tangent line). In this case, the angles are measured with respect to the tangent line, and the same argument used by Heron shows that if \(C\) is such that the angle of incidence equals the angle of reflection, then \(|AC|+|BC|\) is minimized.
Figure 29. Law of Reflection for any concave curve
An interesting application of the Law of Reflection arises in the case of a light beam sent toward a parabolic mirror, where the light beam is parallel to the axis of the parabola. A parabolic mirror is one whose surface is generated by rotating a parabola about its axis. Suppose the parabola has focus \(F\) and directrix \({\mathcal L},\) and that the light beam \(\overrightarrow{GA}\) hits the parabola at \(A.\) Recall from Roberval's construction of tangent lines to parabolas that the tangent line at \(A\) bisects the angle \(\angle FAB.\) Hence \(m\angle 1=m\angle 2.\) Since \(\angle 2\) and \(\angle 3\) are vertical angles, \(m\angle 2=m\angle 3.\) Hence \(m\angle 1=m\angle 3.\) So by the Equal Angle Law of Reflection, the light beam will be reflected in the direction \(\overrightarrow{AF}.\) This will be true for any point \(A\) on the parabola.
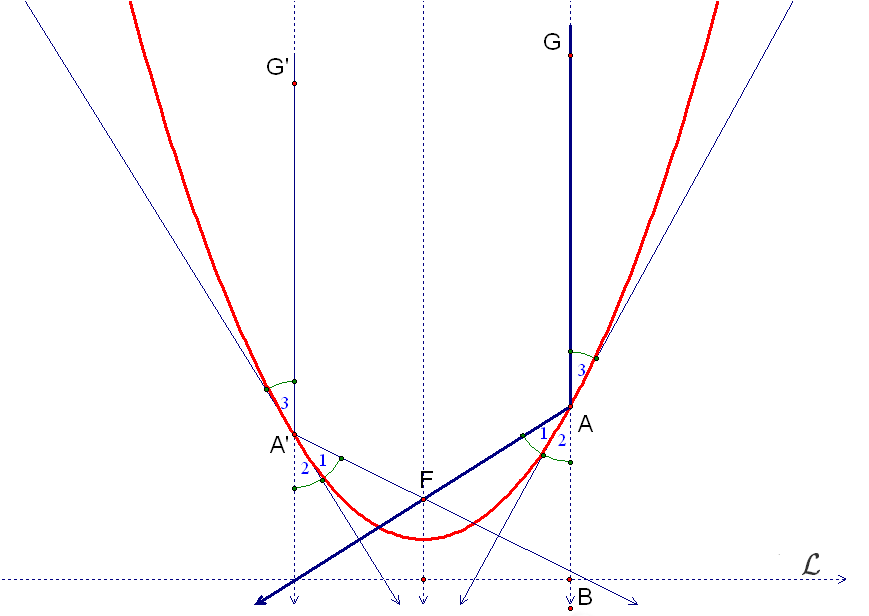
Figure 30. Light rays directed toward a parabolic mirror parallel to the parabola's axis are all reflected toward the focus \(F\) of the parabola.
There is a famous story about Archimedes in which he is said to have used a parabolic mirror to defeat the Roman General Marcellus. Supposedly, he tilted the mirror toward the sun in such a way that all the sun's rays when reflected off the mirror went through the focal point. The heat generated at that point caused a fire to ignite and destroy the entire Roman fleet.
Figure 31. Wall painting from the Stanzino delle Matematiche in the Galleria degli Uffizi (Florence, Italy). Painted by Giulio Parigi (1571-1635) in the years 1599-1600.
Exercises
Figure 32. Euclid's Law of Reflection (applet for Exercise 8)
Exercise 8.
Use calculus and a CAS to find the point \(C\) on the \(x\) axis for which \(|AC|+|CB|\) is the shortest, where \(A=(0,4)\) and \(B=(10,12).\) Use the applet in Figure 32, above, to enter your solution and verify Euclid's Law of Reflection.
Historical Activities for Calculus - Module 3: Optimization – Snell's Law and the Principle of Least Time
Snell's Law and the Principle of Least Time
Euclid's Law of Reflection, formulated around 300 BCE, tells us what happens when a beam of light is reflected off a mirror. The Dutch physicist Willebrord Snell (1580-1626) was interested in the phenomenon of refraction, which is the change in direction that occurs when a beam of light crosses a boundary from one medium (say air) into another (say water). He observed that when the light beam enters the denser medium at some point \(C\) on the line, its velocity decreases and its path bends toward the normal to the line at \(C.\)
Snell's experiments led him to the discovery of the following relationship, known as Snell's Law:
Figure 33. Snell's Law: \(\displaystyle{\frac{\sin \theta_1}{\sin \theta_2}={\rm constant}.}\)
Figure 34. Use this GeoGebra applet to investigate Snell's Law. You can drag \(C\) to determine the approximate location of the point that minimizes the time of travel along the path from \(A\) to \(C\) to \(B.\)
In 1637, Pierre de Fermat became interested in finding a theoretical derivation of Snell's Law. Recall that Heron had shown that if a light beam traveled from \(A\) to \(B\) by first reflecting off a line \({\mathcal L},\) the path taken was the one that would take the minimum time. Fermat reasoned that the same “least time” principle would govern that path from \(A\) to \(B\) across the boundary \({\mathcal L}.\)
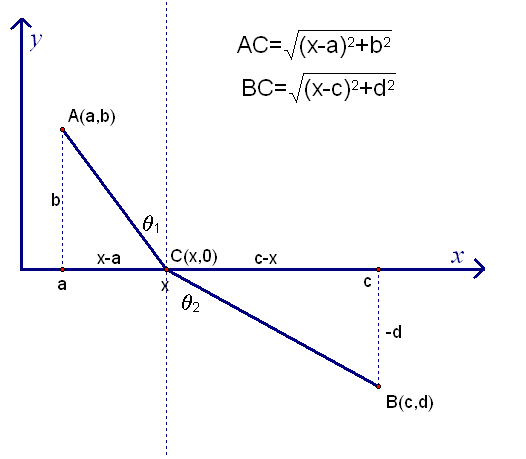
Fermat used the differential calculus (techniques which he himself developed by reasoning that the slope of a tangent line at a local maximum or minimum must be zero) to determine the quickest path. Suppose \(A=(a,b)\) lies above the \(x\)-axis and \(B=(c,d)\) lies below the \(x\)-axis, as in the picture below:
Figure 35. In modern terms and notation, Fermat wished to minimize the time of travel of a light beam along the path from \(A\) to \(C\) to \(B.\)
We wish to find the point \(C=(x,0)\) on the \(x\) axis that minimizes the time of travel of a light beam along the path \(A\) to \(C\) to \(B,\) assuming its velocity above the \(x\) axis is \(v_1,\) and its velocity below the \(x\) axis is \(v_2.\) Since \[\mbox{time}=\frac{\mbox{distance}}{\mbox{velocity}},\] the time of travel is
\[T(x)=\frac{\sqrt{(x-a)^2+b^2}}{v_1}+\frac{\sqrt{(x-c)^2+d^2}}{v_2}\]
If we take the derivative and set it equal to \(0,\) we have
\[\frac{\frac12\left[(x-a)^2+b^2\right]^{-1/2}\cdot 2(x-a)}{v_1}+\frac{\frac12\left[(x-c)^2+d^2\right]^{-1/2}\cdot 2(x-c)}{v_2}=0,\]
which can be rewritten as
\[\frac{x-a}{v_1\sqrt{(x-a)^2+b^2}}+\frac{x-c}{v_2\sqrt{(x-c)^2+d^2}}=0.\]
But since \[\sin\theta_1=\frac{x-a}{\sqrt{(x-a)^2+b^2}}\quad\quad{\rm and}\quad\quad\sin\theta_2=\frac{c-x}{\sqrt{(x-c)^2+d^2}},\] the above equation can be rewritten as
\[\frac{\sin\theta_1}{v_1}-\frac{\sin\theta_2}{v_2}=0\]
or, equivalently,
\[\frac{\sin\theta_1}{\sin\theta_2}=\frac{v_1}{v_2},\]
which is of course Snell's Law. But whereas Snell had conjectured his law based on observation, Fermat succeeded in giving a mathematical proof.
Fermat was led to investigate Snell's Law after reading a paper by René Descartes on the subject. Fermat thought Descartes' work did not make sense, and he could not understand how Descartes was able to arrive at the correct result using faulty and illogical arguments. Indeed, Fermat's criticisms could be interpreted as an accusation that Descartes, who made no mention of Snell in his work, had somehow gotten hold of Snell's experimental data, conjectured the correct law from the data, and then, working backwards, invented an argument that made little sense but led to the correct conclusion. Needless to say, Descartes did not take kindly to Fermat's accusations!
Exercises
Figure 36. Applet for Exercise 9, part a
Exercise 9.
(a) Use calculus (and a CAS if needed) to compute the value of the \(x\)-coordinate of the point \(C\) on the \(x\)-axis that minimizes the time of travel along \(A\) to \(C\) to \(B\) with \(A=(1,3),\) \(B=(4,-2),\) \(v_1=4\) units/sec, and \(v_2=5\) units/sec. Use the applet in Figure 36 to enter your solution to verify Snell's Law.
(b) Repeat part a with \(A=(-3,4),\) \(B=(2,-5),\) \(v_1=1\) unit/sec, and \(v_2=2\) units/sec.
(c) Use calculus and a CAS to find the coordinates of the point \(C\) on the curve \(y=-x^2,\) so that \(|AC|+|BC|\) is a minimum, where \(A=(0,4),\) and \(B=(5,-3).\) Illustrate your solution in GeoGebra, and measure the incidence and reflection angles to verify that they are equal. Your sketch should include the following:
- a plot of the curve \(f(x)=-x^2\)
- a plot of the two points \(A\) and \(B\)
- a plot of the point \(C\) that solves the problem, and
- a graph of the tangent line to the curve at \(C.\)
Historical Activities for Calculus - Module 3: Optimization – L'Hôpital's Pulley Problem
L'Hôpital's Pulley Problem and the Principle of Least Potential Energy
The first calculus textbook was written by the Marquis Guillaume-Francois-Antoine de l'Hôpital (1661-1704). Best known for the famous rule that bears his name that is used to compute limits of indeterminate forms, l'Hôpital was very interested in mathematics and particularly in the new techniques of the calculus that had recently been developed by Isaac Newton (1643-1727) and Gottfried Wilhelm Leibniz (1646-1716). Consequently, he hired one of Leibniz's best students, Johann Bernoulli (1667-1748), to teach the calculus to him. L'Hôpital then took the notes he compiled from Bernoulli's lectures and organized them into a textbook called Analyse des Infiniment Petits. The book contained the original results of Newton, Leibniz, and Johann Bernoulli, as well as Johann's brother Jakob Bernoulli (1654-1705). L'Hôpital has been justly criticized for giving little or no credit to these mathematicians, presenting the mathematics as if it were his own. Indeed, many have suggested that l'Hôpital 's Rule should really be called Bernoulli's Rule, since it was taught to him by Johann! Johann Bernoulli was forced to keep silent during l'Hôpital 's lifetime since l'Hôpital had essentially paid him for the right to use Bernoulli's results in any way he wanted. After l'Hôpital's death, however, Bernoulli began to take credit for practically the entire book.
Being a textbook, Analyse des Infiniment Petits contains a number of interesting problems that are used to demonstrate the techniques of the new calculus. One of these problems is the famous Pulley Problem, illustrated below.
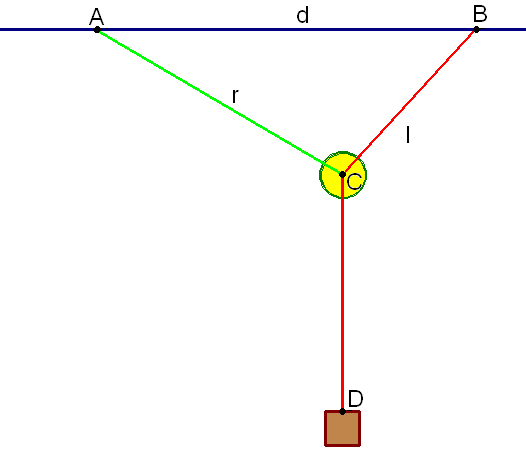
Figure 37. L'Hôpital's Pulley Problem
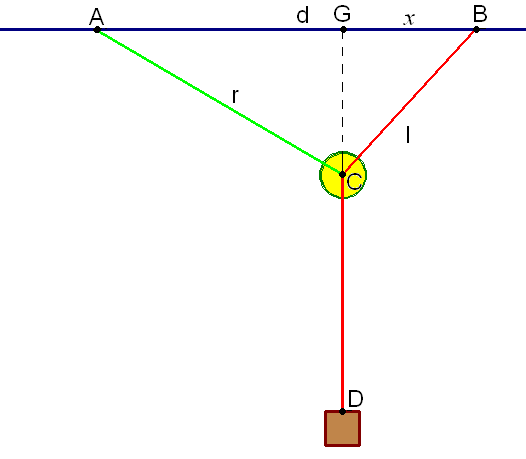
A (weightless) cable of length \(r\) is attached to the ceiling at point \(A.\) The other end of the cable is attached to a pulley at point \(C\). The end of another cable of length \(l\) is attached to the ceiling at point \(B,\) where \(|AB|=d\) and \(d>r\). At the other end of the second cable (point \(D\)) is attached a weight. This second cable passes over the pulley, so \(|BC|+|CD|=l,\) and the whole system is allowed to adjust itself to reach a state of stationary equilibrium. The question is: How far below the ceiling is the final position of the weight? The solution relies on the principle of minimum potential energy. This means that the system will be stable when its potential energy is the least; that is, when the weight hangs as far below the ceiling as possible. Use the applet in Figure 38, below, to explore l'Hôpital's Pulley Problem and identify the approximate equilibrium position for the example shown.
Figure 38. Use this applet to explore l'Hôpital's Pulley Problem.
Exercises
Figure 39. L'Hôpital's Pulley Problem for Exercise 10
Exercise 10.
In Figure 39, above, \(|AB|=d,\) \(|AC|=r,\) and \(|BC|+|CD|=l.\) Let \(x\) be the horizontal distance between \(G\) and \(B.\)
(a) Find an expression for \(|GA|.\)
(b) Find an expression for \(|GC|.\)
(c) Find an expression for \(|BC|.\)
(d) Find an expression for \(|CD|.\)
(e) Find an expression for \(|GD|.\)
(f) According to the principle of minimum potential energy, the system will reach equilibrium when \(|GD|\) is maximized. Use calculus and a CAS to find the value of \(x\) for which \(|GD|\) is a maximum.
(g) Compute \(x\) when \(d=12,\) \(r=7,\) and \(l=14.\)
Figure 38 (repeated from above). Use this applet for Exercise 10, part h.
(h) The applet in Figure 38 illustrates the Pulley Problem. Drag \(C\) to locate the equilibrium position where \(|GD|\) is a maximum. Does \(x=|GB|\) agree with your solution above?
Historical Activities for Calculus - Module 3: Optimization – Regiomontanus' Hanging Picture Problem
Regiomontanus' Hanging Picture Problem
Johann Müller (1436-1476), commonly known today as Regiomontanus, was perhaps the most influential mathematician of the fifteenth century. Although his contributions were mainly in the area of trigonometry, we are interested here in the following problem that he posed in a letter he wrote in 1471:
At what point on the ground does a perpendicularly suspended rod appear largest?
In other words, which point \(P\) on line \({\mathcal L}\) in Figure 40 below maximizes the angle \(APB?\)
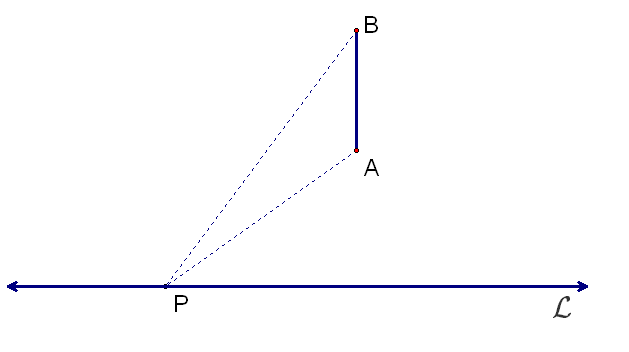
Figure 40. Regiomontanus' Problem: Which point \(P\) on \({\mathcal L}\) maximizes \(m\angle APB?\)
This problem was the first optimization problem that had appeared in the history of mathematics since the days of antiquity. It was probably inspired by questions of perspective that Renaissance artists of that time period were grappling with. It is often stated in modern calculus textbooks as follows:
A painting is hung flat against a wall. How far from the wall should one stand to maximize the viewing angle at his eye subtended by the painting?
Figure 41. Modern equivalent of Regiomontanus' Problem: How far from a wall should an observer stand to maximize his viewing angle \(APB\) (or \(\theta\)) of a picture of height \(|AB|\) on the wall? Use the applet to identify the point \(P\) that maximizes \(m\angle APB\) for the example shown. Drag \(P\) horizontally to adjust the distance of the man from the wall. Next, note that you may adjust as well the height of the man, the height of the picture above the floor, and the height of the picture itself, respectively, by dragging points \(P,\) \(A,\) and \(B\) vertically.
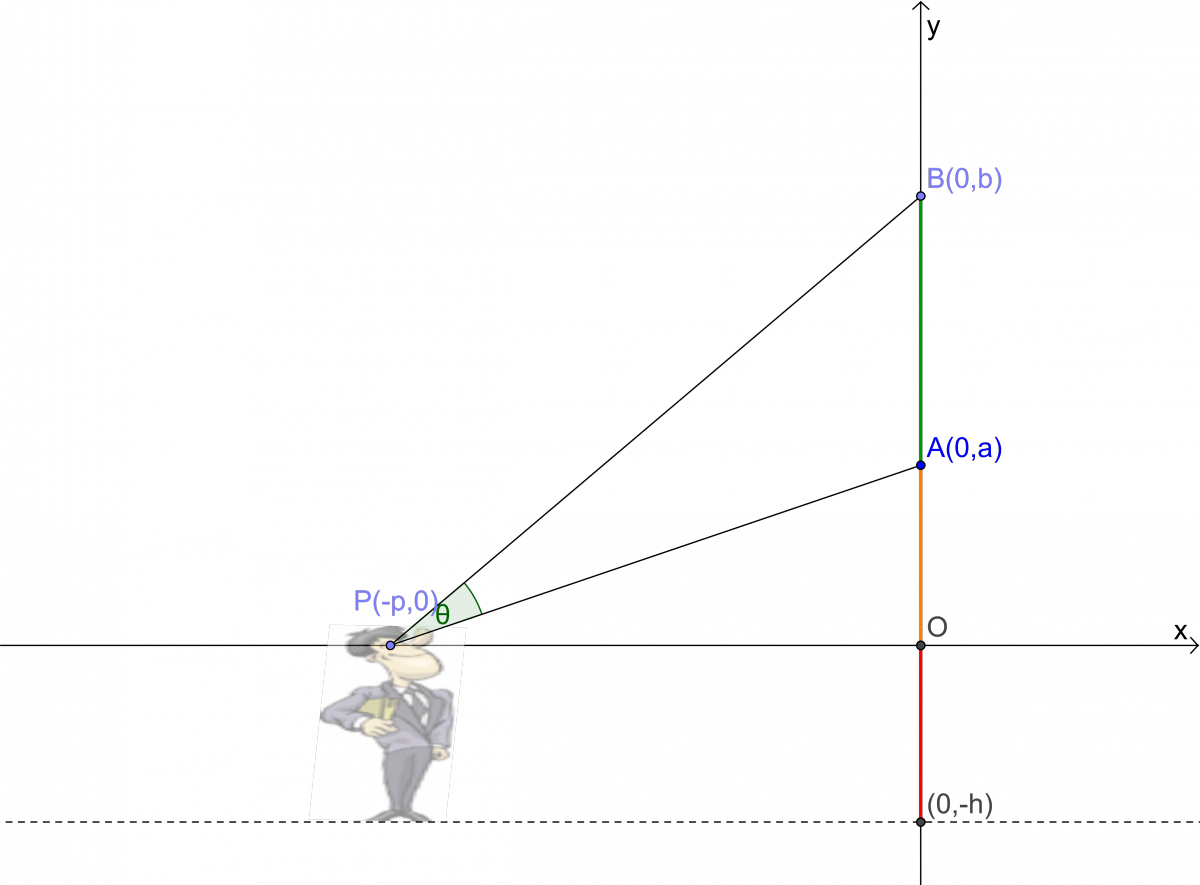
Figure 42. To solve the Hanging Picture Problem more generally, we introduce a coordinate system and assign variables as shown.
In the picture in Figure 42, above, the line \({\mathcal L}\) (from Figure 40) is drawn at the height of the viewer's eye. We can impose a coordinate system on the scenario, with line \({\mathcal L}\) as the \(x\)-axis, and \(A\) and \(B\) (from Figure 40) on the \(y\)-axis, say \(A=(0,a)\) and \(B=(0,b).\) Then the height of the painting is \(b-a\) and the bottom edge of the painting is \(a+h\) units above the floor, where \(h\) is the height of the viewer's eye above the floor.
The original solution to this problem, like Heron's solution to the shortest distance problem, was geometric and did not use calculus. Consider a circle that goes through points \(A\) and \(B\) and is tangent to the line \({\mathcal L}\) (the \(x\)-axis). Let \(P\) be the point of tangency. Then \(P\) is the point on \({\mathcal L}\) that maximizes angle \(APB.\)
Figure 43. Geometric solution to Regiomontanus' Problem: \(P\) should be such that line \({\mathcal L}\) is tangent to the circle through \(P,\) \(A,\) and \(B.\)
To see this, let \(P^{\prime}\) be another point on \({\mathcal L}.\) We claim that \(m\angle 5>m\angle 3.\) Let \(H\) be the point of intersection of the circle and \( P^{\prime}B.\) Then \(m\angle 2=m\angle 5\) since both angles subtend the same chord. Also, \(m\angle 1 +m\angle 2=m\angle 1+m\angle 3+m\angle 4,\) since both equal \(180\) degrees. Subtracting \(m\angle 1\) from both sides gives \(m\angle 2=m\angle 3+m\angle 4.\) Hence
\[m\angle 5=m\angle 2=m\angle 3+m\angle 4>m\angle 3,\]
as was to be shown.
Exercises
Exercise 11.
Use calculus and a CAS to find the solution of Regiomontanus' Hanging Picture Problem. You need to find the value of \(x\) that maximizes \(\theta\) in the diagram below.
Figure 44. Regiomontanus' Hanging Picture Problem for Exercise 11
Here's one way to proceed: Since \(f(x)=\tan x\) is an increasing function, it is equivalent to maximize \[\tan\theta=\tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}.\]
You should be able to rewrite this last expression all in terms of \(x,\) \(a,\) and \(b.\) Then use calculus to find the value of \(x\) that maximizes this quantity.
Exercise 12.
Suppose a six-foot tall adult comes to the museum with his three-foot tall child. They go into a room where a large 12-foot high painting is hung on the wall so that the bottom edge of the painting is 8 feet from the floor.
(a) How far from the painting should each of them stand in order to maximize their individual viewing angles?
(b) Compute each of their maximal viewing angles. Express your answer in degrees.
Figure 45. Applet for Exercise 12, part c. Drag \(I\) to adjust the height of the man. Drag \(A\) and \(B\) to adjust the height of the picture. Drag \(P\) to adjust the distance of the man from the wall.
(c) The applet in Figure 45 illustrates Regiomontanus' Hanging Picture Problem, with the line segment \(AB\) denoting the height of the picture, and the \(x\)-axis representing eye level. Check the box to show the circle through \(A\) and \(B\) tangent to the horizontal axis at eye level. Verify that the point of tangency is the solution to Regiomontanus' Problem by dragging the man's eye to that point and verifying that \(m\angle APB\) equals the maximal viewing angle you found above for the six-foot adult. Repeat for the three-foot child.
Historical Activities for Calculus - Module 3: Optimization – Galileo and the Brachistochrone Problem
Galileo and the Brachistochrone Problem
The last optimization problem that we discuss here is one of the most famous problems in the history of mathematics and was posed by the Swiss mathematician Johann Bernoulli in 1696 as a challenge “to the most acute mathematicians of the entire world.” The problem can be stated as follows:
Given two points on a plane at different heights, what is the shape of the wire down which a bead will slide (without friction) under the influence of gravity so as to pass from the upper point to the lower point in the shortest amount of time?

Figure 46. Brachistochrone Problem: Which path from \(A\) to \(B\) is traversed in the shortest time? (Click image to animate.)
This is the Brachistochrone (“Shortest Time”) Problem. This was a different kind of optimization problem, since instead of asking for the value of a variable, among all possible values, that would maximize or minimize something, it asked for the optimal function (or curve), among all possible curves. The differential calculus does not provide all the tools necessary to solve this problem. So for the moment, we would like to discuss Galileo Galilei's work relevant to this problem, which occurred in 1638, well before the Brachistochrone Problem had been explicitly stated.
Galileo studied motion under gravity, showing that a body falling in space traverses a distance proportional to the square of the time of descent. Using this law, he was able to compute the time of descent of an object falling along an inclined plane from point \(A\) to point \(B,\) assuming no friction.
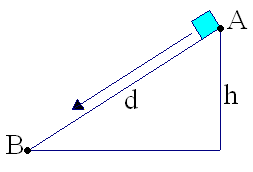
Figure 47. Galileo's formula for time of descent along an inclined plane, as shown in the diagram:
The time to travel from \(A\) to \(B\) is \[\sqrt{\frac{2}{g}}\cdot\frac{d}{\sqrt{h}}\] where \(d\) is the distance between points \(A\) and \(B\) (in meters), \(h\) is the vertical distance between \(A\) and \(B\) (in meters), and \(g\) is the acceleration due to gravity, approximately \(9.80\) \(\mbox{m}/\mbox{sec}^2.\)
Clearly the shortest path from \(A\) to \(B\) is a straight line, but is this path the one that will take the shortest time? For example, is there some point \(C\) such that if the body were to fall following a straight line from \(A\) to \(C,\) and then a straight line from \(C\) to \(B,\) as shown in Figure 48, it would do so in less time than if it traversed a straight-line path from \(A\) to \(B?\)
Figure 48. Does the body fall from point \(A\) to point \(B\) in less time along the path \(A\rightarrow B\) or along the path \(A\rightarrow C\rightarrow B?\)
Galileo appeared to believe that the answer to the brachistochrone problem was an arc of a circle; that is, that the path \(A\rightarrow C\rightarrow B\) in Figure 48 should be replaced by a circle passing through points \(A\) and \(B.\) Was Galileo correct?
Figure 49. Use this GeoGebra applet to explore the Brachistochrone Problem by comparing the times of descent along different polygonal paths.
Exercises
Exercise 13.
Use a CAS to define the following two functions:
\[T(a,b,c,d,u):=\frac{\sqrt{(a-c)^2 + (b-d)^2}\cdot\left(\sqrt{2g(b-d) + u^2}-u\right)}{g(b - d)}\]
\[V(a, b, c, d, u):=\sqrt{2g(b-d) + u^2}\]
where \(g\) has been predefined to be 9.8 (the acceleration due to gravity in meters per square seconds). The function \(T(a,b,c,d,u)\) computes the time of descent from \(A(a,b)\) to \(B(c,d)\) along a straight-line path, assuming no friction and initial velocity \(u.\) The function \(V(a,b,c,d,u)\) gives the terminal velocity. We assume distance is measured in meters and time in seconds.
(a) Compute \(T(0,0,5,-5,0)\) to find the time of descent from \(A(0,0)\) to \(B(5,-5)\) along an inclined plane, assuming no friction and an initial velocity of \(0.\)
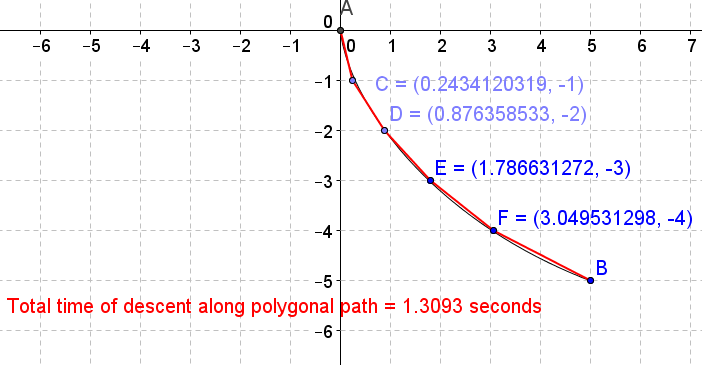
(b) To compute the time of descent along the polygonal path \((0,0)\) to \((1,-2)\) to \((5,-5),\) you need to add the time it takes along \((0,0)\) to \((1,-2),\) which is \(T(0,0,1,-2,0),\) and the time it takes along \((1,-2)\) to \((5,-5),\) which is \(T(1,-2,5,-5,v_1)\) where \(v_1\) is the terminal velocity from the first part of the path, i.e. \(v_1=V(0,0,1,-2,0).\) Hence compute \[T(0,0,1,-2,0)+T(1,-2,5,-5,V(0,0,1,-2,0)).\]
(c) Suppose we want a polygonal path \((0,0)\) to \((x,y)\) to \((5,-5)\) where \((x,y)\) lies on the circle \((x-5)^2+y^2=25.\) Solving for \(y,\) where \(-5\leq y\leq 0,\) we obtain \(y=-\sqrt{25-(x-5)^2},\) so our point \((x,y)\) must be of the form \(\left(x,-\sqrt{25-(x-5)^2}\right)\) in order to lie on the quarter circle. The time of descent for this path then is
\[T\left(0,0,x,-\sqrt{25-(x-5)^2},0\right)+T\left(x,-\sqrt{25-(x-5)^2},5,-5,V\left(0,0,x,-\sqrt{25-(x-5)^2},0\right)\right)\]
Use a CAS and calculus to find the value of \(x\in(0,5)\) that minimizes the above quantity. Compare the time of descent along this polygonal path to the time along the straight line path.
(d) Let \(C\) be the point whose \(x\)-coordinate you found in part 3. Galileo knew that any polygonal path \((0,0)\) to \(C\) to \((5,-5),\) where \(C\) is on the circle, would take less time than the straight line path \((0,0)\) to \((5,-5).\) He then reasoned that if you added another point \(D\) on the circle to form the path \((0,0)\) to \(C\) to \(D\) to \((5,-5),\) the time of descent for this path would be less than the time for the path \((0,0)\) to \(C\) to \((5,-5).\) Find \(D=\left(x,-\sqrt{25-(x-5)^2}\right),\) so that the time of descent for the polygonal path \((0,0)\) to \(C\) to \(D\) to \((5,-5)\) is smallest. What is the total time for the path \((0,0)\) to \(C\) to \(D\) to \((5,-5)?\)
Exercise 14.
(a) Use calculus to find the value of \(x\) so that the time of descent along \((0,0)\) to \((x,-1)\) to \((5,-5)\) is the smallest. Let \(C=(x_1,-1)\) be the point that minimizes the time of descent. Also compute the terminal velocity \(v_1\) on the path \((0,0)\) to \(C.\)
(b) Use calculus to find the value of \(x\) so that the time of descent along \(C\) to \((x,-2)\) to \((5,-5)\) is the smallest, where the initial velocity at \(C\) is \(v_1.\) Let \(D=(x_2,-2)\) be the point that minimizes the time of descent. Also compute the terminal velocity \(v_2\) on the path \(C\) to \(D.\)
(c) Use calculus to find the value of \(x\) that minimizes the time of descent along \(D\) to \((x,-3)\) to \((5,-5)\), where the initial velocity at \(D\) is \(v_2.\) Let \(E=(x_3,-3)\) be the point that minimizes the time of descent. Also compute the terminal velocity \(v_3\) on the path \(D\) to \(E.\)
(d) Finally, use calculus to find the value of \(x\) that minimizes the time of descent along \(E\) to \((x,-4)\) to \((5,-5),\) where the initial velocity at \(E\) is \(v_3.\) Let \(F=(x_4,-4)\) be the point that minimizes the time of descent. Also compute the terminal velocity \(v_4\) on the path \(E\rightarrow F.\)
Figure 50. Diagram for Exercise 14, part e
(e) Compute the time of descent along the the path from \(A(0,0)\) to \(C\) to \(D\) to \(E\) to \(F\) to \(B(5,-5).\) How does this compare to the time of descent along the polygonal path \((0,0)\) to \(C\) to \(D\) to \((5,-5)\) that you computed in the previous exercise?
Figure 51. Applet for Exercise 14, part f
(f) The applet in Figure 51 contains the construction of an (upside-down) cycloid, a curve traced out by a point on the circumference of a circle as it rolls along a straight line. Drag \(C\) to rotate the circle. The curve goes through \(A(0,0),\) but it doesn't go through \(B(5,-5).\) You can find a cycloid that goes through \(B\) by adjusting the radius \(r\) of the rolling circle. What is the radius of the generating circle that produces a cycloid that goes through both \(A\) and \(B?\)
It turns out that this cycloid is the answer to the Brachistochrone Problem for any points \(A\) and \(B,\) not just \(A=(0,0)\) and \(B=(5,-5).\) Add the points on the polygonal path that you found above to the list of points in the applet. Your cycloid should be a pretty good fit.