Historical Activities for Calculus - Module 3: Optimization - Heron's Shortest Distance Problem
Heron's "Shortest Distance" Problem
One of the first non-trivial optimization problems was solved by Heron of Alexandria, who lived about 10-75 C.E. Heron's “Shortest Distance” Problem is as follows:
Given two points \(A\) and \(B\) on one side of a straight line, to find the point \(C\) on the line such that \(|AC|+|CB|\) is as small as possible.
Thus in Figure 26, below, one possible point \(C\) is shown, as well as the length of the path \(A\) to \(C\) to \(B.\)

Figure 26. A possible path from \(A\) to \(B\)
Figure 27. Use this GeoGebra applet to explore the solution to Heron's problem. You can drag \(C\) to determine the approximate length of the shortest path attainable.
To solve this problem mathematically, Heron noticed that if \(B\) is reflected across the line, to say \(B^{\prime},\) then for any point \(C\) on the line, \(|CB|=|CB^{\prime}|,\) and hence minimizing \(|AC|+|CB|\) is equivalent to minimizing \(|AC|+|C B^{\prime}|.\) But clearly since the shortest path from \(A\) to \( B^{\prime}\) is a straight line, the point \(C\) that minimizes \(|AC|+|C B^{\prime}|\) should be the point of intersection of the line with the line segment \(AB^{\prime}.\) Any other path, such as \(A\) to \(C^{\prime}\) to \(B^{\prime},\) will clearly be longer.
Figure 28. Heron's solution of the “Shortest Distance” Problem
Note that \(m\angle 2=m\angle 3\) by construction, and \(m\angle1=m\angle 3\) since these are vertical angles. Therefore, \(m\angle 1=m\angle 2.\) This is the equal angle law of reflection. It was Euclid who, over three hundred years earlier, had noted the now well-known Reflection Law for light:
Equal Angle Law of Reflection (or Euclid's Law of Reflection). If a beam of light is sent toward a mirror, then the angle of incidence equals the angle of reflection.
Heron appears to have been the first to observe that the Reflection Law implies that light always takes the shortest path.
As a matter of fact, the mirror in the Equal Angle Law of Reflection need not be flat. We may replace the line in Heron's problem by any concave curve (a curve is concave if it lies entirely on one side of any tangent line). In this case, the angles are measured with respect to the tangent line, and the same argument used by Heron shows that if \(C\) is such that the angle of incidence equals the angle of reflection, then \(|AC|+|BC|\) is minimized.
Figure 29. Law of Reflection for any concave curve
An interesting application of the Law of Reflection arises in the case of a light beam sent toward a parabolic mirror, where the light beam is parallel to the axis of the parabola. A parabolic mirror is one whose surface is generated by rotating a parabola about its axis. Suppose the parabola has focus \(F\) and directrix \({\mathcal L},\) and that the light beam \(\overrightarrow{GA}\) hits the parabola at \(A.\) Recall from Roberval's construction of tangent lines to parabolas that the tangent line at \(A\) bisects the angle \(\angle FAB.\) Hence \(m\angle 1=m\angle 2.\) Since \(\angle 2\) and \(\angle 3\) are vertical angles, \(m\angle 2=m\angle 3.\) Hence \(m\angle 1=m\angle 3.\) So by the Equal Angle Law of Reflection, the light beam will be reflected in the direction \(\overrightarrow{AF}.\) This will be true for any point \(A\) on the parabola.
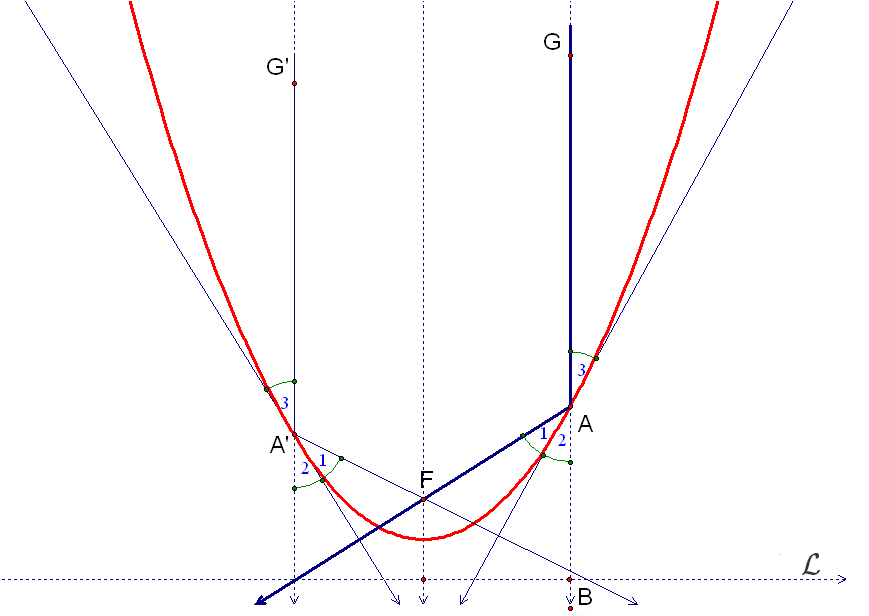
Figure 30. Light rays directed toward a parabolic mirror parallel to the parabola's axis are all reflected toward the focus \(F\) of the parabola.
There is a famous story about Archimedes in which he is said to have used a parabolic mirror to defeat the Roman General Marcellus. Supposedly, he tilted the mirror toward the sun in such a way that all the sun's rays when reflected off the mirror went through the focal point. The heat generated at that point caused a fire to ignite and destroy the entire Roman fleet.
Figure 31. Wall painting from the Stanzino delle Matematiche in the Galleria degli Uffizi (Florence, Italy). Painted by Giulio Parigi (1571-1635) in the years 1599-1600.
Exercises
Figure 32. Euclid's Law of Reflection (applet for Exercise 8)
Exercise 8.
Use calculus and a CAS to find the point \(C\) on the \(x\) axis for which \(|AC|+|CB|\) is the shortest, where \(A=(0,4)\) and \(B=(10,12).\) Use the applet in Figure 32, above, to enter your solution and verify Euclid's Law of Reflection.


