Introduction

In the 21st century we are well-acquainted with the use of dice as randomizing devices for playing board games. We have been entertaining ourselves with such games for centuries. Indeed, in Monopoly, one of the most beloved board games of our era, players move around a board according to the rolls of dice and acquire, sell, and rent properties as they proceed. The goal of the game is to become the "wealthiest" of the players by monopolizing the available properties and bankrupting one's opponents. In Dungeons and Dragons, another wildly popular role-playing game, participants use polyhedral dice to advance play.

Would you be surprised to learn that another game of dice, the Ludus Regularis (Canonical Game), was created in medieval France more than a millennium ago by Wibold, the archdeacon of Noyon, for the diversion and moral instruction of Christian clergy? And while there is no evidence that Wibold had any influence on the 20th century American inventors of Monopoly (see note 1) or Dungeons and Dragons, the existence of such a modern-looking board game at such an early date attests to the appeal of this sort of diversionary activity, one that employs dice to introduce chance variation into a sequence of plays based on simple rules.

Although board games are known to have been played with dice during the Middle Ages in Europe, generally very little is known of the rules of play of many of these games. Some appear to have been games of capture, like chess or checkers, but with moves dictated by the roll of dice. Others may have been games of chase like backgammon in which the goal is to race the other players around the board toward a finish line. The game to be described here, Ludus Regularis, seems to be unique in its structure for its time.

Concerning the Use of Dice

Dice, as randomizing devices, were used in the ancient world in games of chance for the enjoyment and diversion of players but also as means of divination to discern the will of the gods (or God). Casting of lots by means of dice or knucklebones was used to render decisions, the petitioner believing that a supernatural power was speaking through the dice. Pausanius (c. 110 - 180 CE) in his Guide to Greece described the shrine of Heracles at Bura where four knucklebones were cast to determine an oracle which was consulted by the supplicant. There are numerous examples describing such practices in medieval Europe as well.

Consider the Sortes apostolorum (Oracles of the Apostles) of tenth century France [7]. The petitioner consulted one of 56 oracles (see note 2) determined by reference to the outcome of the cast of three cubical dice. The last of the listed oracles, the one corresponding to the outcome of "1" on each of the three dice, was (see note 3):

These are the lots of the saints which are never mistaken, nor do they deceive, and so pray to God, and you will obtain what you desire. Give Him thanks.

As today, gambling was viewed by many in medieval Europe as a vice which led to idleness, sexual promiscuity, parasitism, and crime. Attempts to proscribe gambling have always failed, then as now. It was generally condemned by Church councils from the first centuries of the Christian era. Indeed, what is conjectured to be the earliest papal encyclical was devoted exclusively to theological arguments against the evils of dicing. The encyclical, De Aleatoribus (Concerning dicing), was formerly attributed to St. Cyprian of the mid-third century, but was possibly written by Pope St. Victor of the late second century. Regardless of its authorship, it was composed no later than the fourth century.

What was proscribed of the faithful was especially forbidden to clergymen. The Regulæ ecclesiasticæ sanctorum apostolorum (Ecclesiatical Regulations of the Holy Apostles), attributed to Dionysius Exiguus (see note 4), which regulated the behavior of clergy, was important in this regard. Here we find, in particular [8],

Canon 42: A bishop, or priest, or deacon devoting himself to dicing and drunkenness must either desist or be certainly condemned.

Canon 43: A subdeacon, or reader, or cantor, doing likewise either must desist or be excommunicated; likewise, even the laity.

In 774, Pope Adrian I issued a collection of these canons to the emperor Charlemagne who adopted them as laws of his empire in 802 for the purpose of raising the morals of the clergy at the Synod of Aachen [6].

The dicing to which the canons spoke is thought to be derived from the Roman game of alea (later called tabula), a board game ancestral to today's backgammon, which was played with three cubical dice [15].

---

Notes

1. Monopoly is produced and marketed by the American game and toy company Hasbro.

2. The reason for 56 oracles will be explained later.

3. Hæ sunt sortes sanctorum quæ nunquam falluntur, nec mentiuntur, id est Deum roga, et obtinebis quod cupis. Age ei gratias. Translation of this and other Latin texts quoted in this paper are by the authors.

4. Dionysius Exiguus is also known as Dionysius the Short, perhaps best known for having invented "Anno Domini," Christian era dating, to replace the Roman imperial method that was in use in his time.

Wibold and His World

The chronicler Balderic (c. 1017-1095), in his history of what is today northern France, introduced Wibold and his Canonical Game in this way  [2, Chapter 88]:

Wibold, Archdeacon of the church at Noyon, a man evidently given sufficient instruction as much in secular as in ecclesiastic studies succeeds [upon the death of Ansbert]. Accordingly he has skillfully constructed a canonical game for the clerics who are fond of dice games. Namely, by exercising themselves with learned leisure, they may become accustomed to overcome vices with charity, and evade a worldly and quarrelsome form of dicing.

Balderic included a lengthy description by Wibold himself of the aims and rules of his game, which we shall present in succeeding pages.

Little is known of Wibold's life. He was born at Cambrai toward the beginning of the 10th century. As archdeacon of Noyon, he supervised and had the power to discipline the clergy of the diocese. The unified acclaim of the people and its clergy caused him to be recommended in 965 for the bishopric of Cambrai and Arras. His position was accepted by Holy Roman Emperor Otto I without difficulty. However, Wibold believed that he needed to take himself to Otto in order to receive some sort of investiture. So he traveled to Italy at the height of the summer of 966. It was there that Otto presented to him authority over Cambrai, an office which then remained in Wibold's family for generations. Unfortunately, the strain of this travel was too much for him and he died shortly after returning to Cambrai [1].

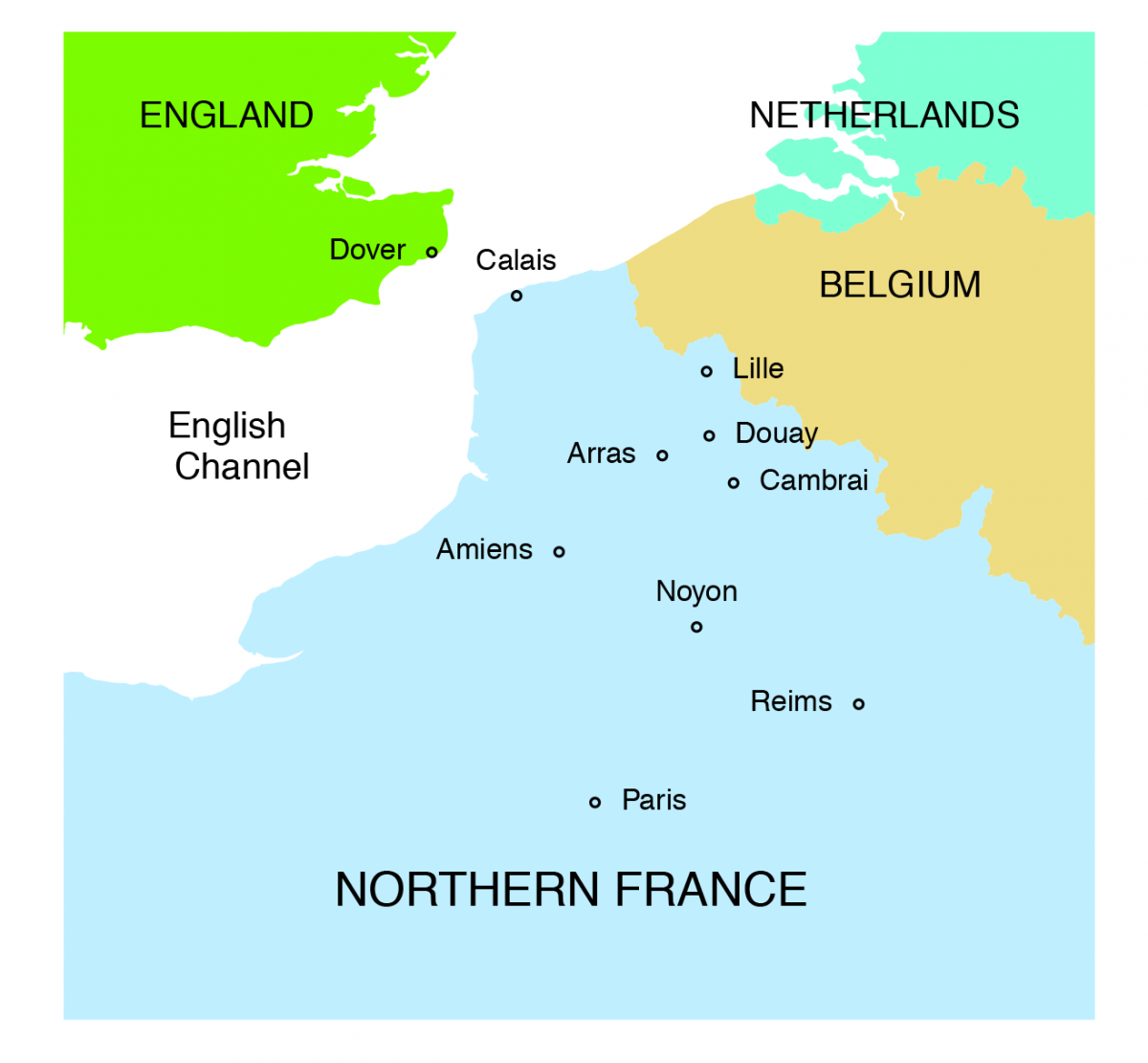Cambrai, where Wibold was born and named bishop, is located in northern France near today's border with Belgium in a region then known as French Flanders. To the northwest lies Arras and, ultimately, the Straight of Dover at Calais. Noyon, which lies approximately midway between Cambrai and Paris, was an important city in Wibold's day – Charlemagne was crowned at its cathedral in 768; Hugh, first in the House of Capet, received his crown there as King of the Franks in 987.

All was not calm in mid-tenth century northern France. Charlemagne's empire had collapsed by this time. During the previous century, the Norse had invaded and ravaged Noyon and Cambrai. Magyars entered the region from central Europe, burning villages surrounding Cambrai in 954. But despite these problems, Cambrai and Arras both thrived as centers of trade.

Otto I, who defeated the Magyars in 955, was crowned Holy Roman Emperor by Pope John XII at Rome in 962. The region about Cambrai then became part of his empire. To establish his influence, Otto granted the bishop at Cambrai temporal powers over the city. In 1007, during the reign of Henry II, it became a small state within the empire and was governed by its bishop.

This period marked a low point for the Church and papacy in Europe. Political corruption within the Church led to calls for significant reform. One such movement was led by St. Odo, who became abbot at Cluny in 927. Odo's reforms spread throughout France, Italy, Spain and England. An important aspect of these reforms was to remove interference by the local rulers in the monasteries. Nonetheless, for several centuries thereafter rulers throughout Europe successfully manipulated bishops and popes for political gain.

Note on Sources

Our source for Wibold's game is a history of the bishoprics of Arras and Cambrai, communities in northern France. The history was compiled by a certain Balderic or Baudri (Latin Baldericus, c. 1017 - c. 1097), who was known as cantor of Thérouanne [3]. His work, Chronicon Cameracense et Atrebatense (Chronicle of Cambrai and Arras), covered the period from the time of Julius Caesar to the year 1075. It was first printed in the year 1615 [2]  under the editorship of George Colvener (1564 - 1649), a Flemish theologian who was provost and chancellor at the University of Douay. In 1834 a new edition was published based upon a comparison of three manuscripts by André Le Glay [13]. The following year a French translation by Faverot and Petit appeared as Chronique de Balderic [16]. The best edition is that found in Monumenta Germaniæ Historica VII (series editor Georg Pertz, 1846) where it is entitled "Gesta episcoporum Cameracensium," edited by Ludwig Bethmann [4].

The Ludus Regularis

Wibold likely invented his dice game while he was archdeacon at Noyon, France, in the mid tenth century. Canon law forbade clerics to engage in gambling because of the vices associated with it. But Wibold had the idea to co-opt the temptation of gambling and turn it to the promotion of and instruction in virtuous living, thereby permitting clerics to take part in a pleasurable activity while at the same time improving themselves. The game is called both Ludus regularis seu clericalis (the canonical or clerical game) and Alea regularis contra alea secularis (the canonical game of dice as opposed to the secular game of dice). The rules of the game in the words of Wibold himself were preserved by the historian Balderic in the same Chronicon (Chronicle) mentioned above.

Our excerpt of Wibold's account begins with a reference to the canons listed in the section, "Concerning the Use of Dice," and justifies his creation of the game:

. . . Therefore because the same [canonical] rule prohibits clerics to be gamblers---seeing that a game of dice invented by men, perfidious and also deprived of the expectation of good things, is used perversely---as it is a cause of discord, perjuries and other vices: it is very appropriate that having abandoned vices according to the [canonical] rule, [clerics] cast lots for themselves in order to acquire virtues. Therefore it is pleasing that from the same dice play which we have mentioned above, there also be arranged a certain clerical game that for this reason we should  call regular, not for the sake of mocking a certain rule, but rather for the sake of training [the players in the cultivation of virtue]. . . .

Association of the Lots with Virtues

Let us consider how Wibold described his numbering of the virtues [2].

Thus set down Charity named with its various offspring, and, as means of governing, let us furnish individually and with each one of the lots of the die [their] corresponding numbers, lest one be unable to discover what is being associated by this [method]; then examine that [lot], and here is shown what is possible. (See Table 1, below.)

Accordingly from the first [row] putting the ones first, and proceeding through the twos and the others up to the sixes, by means of a three-fold cycle of these [numbers] among themselves, it contains the Twenty Daughters of the Holy Mother, and it ends with Wisdom. And afterwards the twos starting with Remorse, fifteen of them to Reverence; from this the threes, from the first, Piety, 10 [of them], to Exomologesis (see note 5); and thus the fours from Maturity, 6 [of them], to Lamentation;  with likewise the fives, from Cheerfulness, bringing in 3 [of them]; it is concluded at the end by Self-control. Indeed the last, composed of sixes, as the first, rejoices in simplicity; it possesses the guardian of the virtues, Humility. Which all at once together become 56.

And if we consider more carefully, we shall see that this progression of numbers, from three ascending to eighteen, brings together the virtues, each of the virtues with its own [mate]. Certainly the first, and the second are joined respectively with the last and the second to last; the third, and the second to last, two each; each among themselves are joined, similarly as the first and last, all the way to the four [groups of] six in the middle; [other groups] comprise three, four or five virtues, and in turn with each other always render [in sum] the number twenty-one. These are therefore

• 3, 4, matched with 17 and 18, respectively: namely, Charity, Faith with Self-control, and Humility;
• 5 and 16, two apiece: which are Hope and Fortitude with Lamentation and Compassion;
• 6 and 15, three apiece: Justice, Peace, and Remorse with Exomologesis, Longing and Cheerfulness;
• 7 and 14, four apiece: Prudence, Chastity, Fear, and Joy with Reverence, Contrition, Constancy, and Understanding;
• 8 and 13, five apiece: Temperance, Mercy, Foresight, Sobriety and Cleverness with Wisdom, Virginity, Mortification, Innocence and Concern;
• 9 and 10, 11 and 12 distinguish six apiece: Obedience, Discretion, Goodness, Satisfaction, Simplicity, and Piety; Perseverance, Modesty, Sweetness, Hospitality, Patience and, of course, Indulgence; with Long-suffering, Gentleness, Economy, Zeal, Prayerfulness, likewise also Judgment; Liberality, Poverty, Mildness, Love, Vigilance and by all means Maturity.

Figure 1. First half of Wibold's Table of Virtues [2] (Source: Google Books)

Enumeration of Outcomes

An examination of Figure 1, or its representation in Table 1, makes clear what Wibold described. The triple of numbers placed to the left of each virtue represents the outcome of a roll of three cubical dice. The number to the right of each virtue is the sum of these same three numbers.

Table 1 permits some speculation as to the appearance of a game board. Two of several possible arrangements appear as Tables 5 and 6 in Possible Game Boards later in this article.

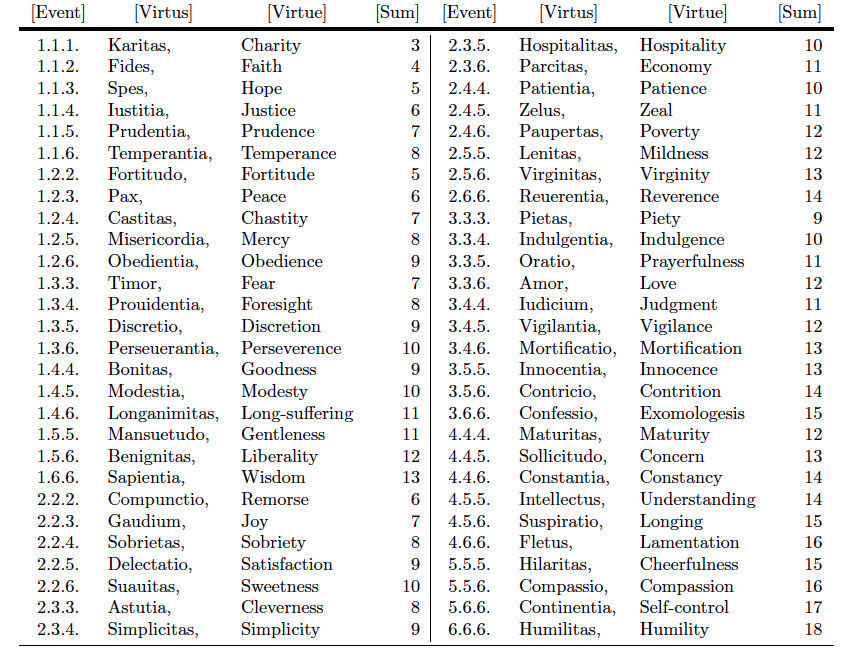
Table 1. Wibold's Table of Virtues, with English translation of virtues added

Suppose we denote the dice, which are clearly cubical, whose faces are marked with the numbers 1, 2, 3, 4, 5, and 6, and which we assume to be distinguishable from one another in some manner, by \(A\), \(B\), and \(C\). Let \(a\), \(b\), and \(c\) or, better, the ordered triple \((a,b,c)\), denote the outcome of the roll of the dice \(A\), \(B\), and \(C\), respectively. Standard dice have been designed for millennia so that opposite sides always sum to \(7.\) Thus there is a one-to-one correspondence between \((a,b,c)\) and the complementary outcome \((7-a,7-b,7-c)\). This observation will be exploited later.

There are then clearly \(6^3=216\) distinct equiprobable outcomes if three (fair) dice are cast. We can enumerate them with the expanded product
\[P=(x+x^2+x^3+x^4+x^5+x^6)(y+y^2+y^3+y^4+y^5+y^6)(z+z^2+z^3+z^4+z^5+z^6).\] A typical term in \(P\) is the product of one term from each of the three factors and, therefore, it must have the form \(x^ay^bz^c\). This term can be understood as representing the outcome \((a,b,c)\).

In the play of the game, however, the three dice are not distinguishable; for instance, the dice rolls \[(1,4,5), (1,5,4), (4,1,5), (4,5,1), (5,1,4), (5,4,1)\] are all considered the same outcome. Thus, to determine the number of ways in which each sum of the faces of dice may be obtained, we replace \(x\), \(y\), and \(z\) in the polynomial above by a single symbol, say \(t\). Each coefficient of the new polynomial \((t+t^2+t^3+t^4+t^5+t^6)^3,\) after being expanded, gives the number of ways of obtaining the sum represented by the corresponding exponent, since \(x^ay^bz^c=t^{a+b+c}\). The expansion of the polynomial in \(t\) is
\begin{equation*}\begin{split}
t^3&+3t^4+6t^5+10t^6+15t^7+21t^8+25t^9+27t^{10}\\&+27t^{11}+25t^{12}+21t^{13}
+15t^{14}+10t^{15}+6t^{16}+3t^{17}+t^{18}.
\end{split}\end{equation*} We can now read off the number of ways to achieve a given total \(n\) as the coefficient of the term \(t^n.\) Thus, for example, there are \(21\) ways to achieve each of the complementary totals of \(8\) or of \(13,\) but only \(10\) ways to achieve each of \(6\) or \(15.\)

Wibold's Cyclic Arrangement

Wibold sought a systematic enumeration of all the lots. (See Figure 1, above.) We see that he made use of a cyclic arrangement in order to enumerate the outcomes of the dice. He constructed his list beginning with the triple \((1,1,1)\) and terminating with the triple \((6,6,6)\) according to the following system:

Every outcome may be represented as a triple \((a,b,c)\) where, because of the indistinguishability of the dice, we always have \(a\leq b\leq c\). Wibold listed the outcomes by using standard lexicographic order: \[(1,1,1)\prec(1,1,2)\prec(1,1,3)\prec\cdots\prec(1,1,6)\prec(1,2,2)\prec\cdots\prec(1,2,6)\prec(1,3,3)\prec\cdots\] He therefore counted a total of 56 triples.

To see this, we might instead note that three types of events can occur:

• All faces are the same;
• two faces are the same but the third is different;
• all faces differ.

It is easy to enumerate the outcomes when all faces show the same: \((1,1,1),\) \((2,2,2),\ldots,(6,6,6),\) six ways in all.

When exactly two faces are the same, we note that three different arrangements of the same numbers occur, say \((a,a,b)\), \((a,b,a)\), \((b,a,a)\), all of which are equivalent. Since there are \(6\) choices for \(a\) and \(5\) for \(b\), each of these three arrangements may be formed in \(6\times5=30\) ways. In all, \(90\) of the \(216\) outcomes are of this type. But, since outcomes of this type are equivalent in sets of \(3,\) there are only \(30\) distinct outcomes of this type.

If all three faces differ, six different permutations may be formed of the numbers: \((a,b,c)\), \((a,c,b)\), \((b,a,c)\), \((b,c,a)\), \((c,a,b)\), \((c,b,a)\), all of which are equivalent outcomes. A permutation of six numbers taken three at a time can be formed in exactly \(6\times 5\times 4=120\) ways. But because the permutations are equivalent in sets of \(6,\) there are only \(20\) distinct outcomes. This gives us a total of \(6+30+20=56\) distinct outcomes.

There is a quicker way to count the distinct outcomes. If we denote by \({}_nW_k\) (with \(W\) chosen to honor Wibold) the number of distinct outcomes when sampling \(k\) items with replacement from a set of size \(n\) where order is ignored, then \[{}_nW_k=\binom{n+k-1}{k}\] (For a discussion of this formula, see [12], for instance.) For Wibold's game, \({}_6W_3=\binom{8}{3}=56\).

Table 2. Ways to achieve each sum with associated multiplicities

Wibold was interested in the sum of the three faces, but he also realized that the opposing face on each cube is complementary; that is, outcome \((a,b,c)\) opposes outcome \((7-a,7-b,7-c)\). Thus it suffices to enumerate outcomes only for values of the sum from \(3\) to \(10.\) Rolls summing from \(11\) to \(18\) can be placed in one-to-one correspondence with those summing from \(10\) to \(3\), respectively, so their counts are correspondingly identical. In Table 2, we use the notation \((a,b,c)_k\) to indicate that there are \(k\) permutations of the numbers \(a\), \(b\), and \(c\).

What may be gleaned from Table 2, above, is that not all ways to achieve a certain sum are equally likely. Let's consider, for example, the sum \(6.\) JUSTICE comes from the outcome \((1,1,4)\) and is given in three ways, PEACE, \((1,2,3),\) in six ways, and REMORSE, \((2,2,2),\) in only one way.

---

Note

5. Exomologesis refers to the public confession of sins.

Wibold's Number Mysticism

The Pythagoreans believed that All is number. This idea was developed in the works of Greek, Roman, Jewish, Christian and Islamic philosophers and theologians through the medieval period. Numbers and a particular calculus of numbers, called arithmology, were seen to be the key to understanding the world. From arithmology arose a theology of arithmetic. Indeed, "medieval [Christian] theology was very largely concerned with attempts to establish the numerical relationships of the supermundane, ecclesiastical and temporal worlds" [11].

The Greek arithmetical tradition was passed to the West primarily through the De Institutione Arithmetica of Boethius (6th century) in which he investigated fundamental Pythagorean number theory (e.g. unity in multiplicity, evenness and oddness, deficient, perfect, and abundant numbers). This work was a simplification of the Introduction to Arithmetic of Nicomachus of Gerasa (2nd c.). Christian writers such as Augustine of Hippo (4th c.), Isidore of Seville (7th c.), and Rabanus Maurus (9th c.) incorporated the number theory of Boethius into a theological discourse. These mathematical concepts lent a mystical authority for identifying relationships amongst theological concepts.

In the next section of text, Wibold called on this tradition when he commented on his pairings of sums of dice rolls [2].

And let us respond through each individually:

• Concerning the [sum] three, by virtue of the very one-ness of the first of these [things], shall we not designate the name of the Holy Trinity?
• But what for [the sum] four if not the trumpets of the four Evangelists?
• These likewise taken together demonstrate that most holy sevenfold grace, full of charismatic gifts. Indeed seven regarded twice, and added to three is 17, and to four 18. (Note in what manner 3, 7 and also 4 return to themselves.)
• In addition we can ascribe to 10 the Ten Commandments, which work under the former law, and now under grace, and to 8 the eighth age, which is not yet come.

But it is fitting to keep in mind these three [numbers 3, 4, and 7] in a manner besides. Therefore, he, who on hearing the blare of the trumpets of the holy Gospels, venerates the Holy Trinity with most intimate love of his heart, and is eager to behold with sevenfold grace as far as the end [of time], he seeks to have

• Charity, in which the whole law is fulfilled,
• Faith, without which it is impossible to please God,
• Continence, in order that he abstains himself from vices, by which he may prevail to hold fast virtues,
• Humility, without which, he who gathers virtues is as if he carries dust in the wind;

let him busy himself to exercise his disposition charitably, faithfully, temperately, and humbly, if he seeks to arrive to an accumulation of the [virtues] (see note 6).

A number of paragraphs of text follow in which Wibold invoked similar number mysticism for the remaining pairs of sums of rolls of dice. Omitting any more of this, we return to Wibold's game mechanics: a description of the dice, the rules of play, and who wins the game.

---

Note

6. Wibold here referred to the virtues (Charity, Faith, Continence, and Humility) associated with rolls of 3, 4, 17 and 18.

Wibold's Dice

Having established the various outcomes of rolling three dice and the corresponding virtues, Wibold described the design of the dice for his Ludus Regularis [2]:

Therefore because we have ordered the virtues and the numbers in a certain way, let us determine now in what manner they should arise by lot. Thus let us take three dice, which have six faces apiece, with various numbers inscribed – where the greatest is six (see note 7); the other remaining [faces] always one fewer, all the way to the ace, which taken together make 21 (see note 8); also, with our 5 vowels, namely  A, E, I, O, U, let us decorate each [die] in the same order, so that the same [sequence of letters] repeated four times is set out upon each; and by continuing this process with a sustained and even course of movement, beginning at the ace there is written in the first place [on the first die] A, on the second E, the third I, always in direct sequence; and [the sequence] ends with the same letter [with which it began], thusly:

Thus having set forth these things, we desire that, by means of these three [dice], numbers be sought which are computed exactly as the lot will have dictated [and] always in its [designated] order, just as one is used to playing in the aforementioned dice game. Indeed we have omitted \(\Upsilon\), the sixth Greek vowel, not only because we so little require it within language and because we do not observe fully our rules of orthography, but because we desire of the work (see note 9), to profitably  and commonly cultivate our sense of enjoyment.

A second use of cyclic arrangements occurs in the construction of the cubical dice. The pips that appear on each face of the dice are composed of the vowels A, E, I, O, U. Wibold instructs us to write the sequence AEIOU over and over, forming from it in sequence blocks of length 1, 2, 3, 4, 5 and 6 to create the labeling of the faces of the first die, then we repeat the process to create the labeling of faces for the second and third dice.

\[\underset{\text{Die 1}}{\underbrace{\text{\(|\)A\(|\)EI\(|\)OUA\(|\)EIOU\(|\)AEIOU\(|\)AEIOUA\(|\)}}}
\underset{\text{Die 2}}{\underbrace{|\text{E\(|\)IO\(|\)UAE\(|\)IOUA\(|\)EIOUA\(|\)EIOUAE}|}}\]
\[\underset{\text{Die 3}}{\underbrace{|\text{I\(|\)OU\(|\)AEI\(|\)OUAE\(|\)IOUAE\(|\)IOUAEI}|}}\] We may assume that these dice are constructed in the usual manner so that the sum of the pips on the opposing faces is always 7 (see note 10).

Wibold then proceeded to place consonants on another die. An inspection of Figure 1, Wibold's Table of Virtues, shows that the letter U represented a consonant (which today we write as V) whenever it did not appear as an initial letter of a word. This occurs, for example, in REUERENTIA. The letter U was both a vowel and a consonant in the Latin alphabet. Similarly, the letter I represented both the vowel and the consonant now written as J. Note, for example, IUSTITIA. He continues:

Seeing that there remain sixteen [letters] in the alphabet, all the rest are consonants, – with the exception of Q, which the grammarians call unnecessary, and which for that reason we have not counted, because absent its traveling companion, namely U, the letter loses its force, which can be very easily understood (see note 11); moreover, it is the seventeenth number for the completion, which we considered as though it were an extra [letter], – therefore in the same way it is proper to insert the vowels on a square [face], thus it is proper to insert the consonants on a single triangular pyramid, which has four faces, thus:

We see that Wibold omitted the consonant V and consonant I from the die. We conjecture that this is because both letters had been accommodated as vowels.

Game Play

Having constructed the dice, Wibold then described how to play the game:

By rule, what is held on the die, if it be any one of the consonants which has separated the vowels in the name of the virtue that is found underneath it, it is reckoned to stand for all the other [consonants]; moreover [whereas] what is on its square-side (see note 12) will be revealed on the upper face, here (see note 13) it is that which is on the lower [face], on its base.

. . . Thus when the cubes have been cast from the hand together with the triangle (sic), and with their letters individually inspected, then one will have recourse to the margin (see note 14), [where] the numbers [are] set adjacent to the virtues.

And in the same way as before, we should similarly record the separation of the three-fold [lot] into the individual vowels so found, which will be the virtue obtained alongside, its  vowels having been made apparent; if we are successful in  constructing [the virtue] with the vowels, and thus are in private possession of it, then partners playing with us may in no way prevail to claim the same one for themselves in the same game.

In any case, the dice in their whimsy, each by rolling and alternating in turn, [rendering] judgment, distribute all the virtues by lot; and if they [virtues] do not divide in mutually equal measure, those who will have gained more – even [just] one more – than the others should rejoice to have been granted preference with respect to the others.

Therefore as far as this is concerned, if it is necessary [to do so], then Charity, which is worth double, should be reckoned for two virtues; which  furthermore, on account of the eclipse of just one letter, namely A, one should examine a second cast after the first – which we prohibit from happening in all other circumstances.

And until the sixth hour (see note 15) of that day, those [who are] more eminent, who call their lessers pupils, should urge that the virtues which are lacking to them by the lots, they should busy themselves to procure by good habits. Also the lessers, recognizing the equanimity (see note 16) of the dice, and just as . . . with preference being offered to them as tutors, so should they be prepared to call [the more eminent ones] teachers.

And if it should happen that no one is able to win over another, all those possessing virtues, with equanimity each in respect to another, then in charity alone they should always be united, and give thanks in the name of fraternity. – The same can happen in another more effective and pleasant manner perhaps for some [players], by which, with each of the three [cubical] dice only having been tossed, and referring back not to the power of the elements but to their sum taken together simultaneously, however many of this kind one obtains corresponding to [this] number, as has been inspected, he will boast to possess for himself [all those] virtues.

We propose these to you reader in such a way, that if what the pen completes, usefully you should adopt, or you should subtract by correcting; nevertheless you should promote no blasphemy; and if you are unwilling to approve, you must not disparage. Because if the game makes no sense [to you], or [if] it brings forth disgust from the soul, [then] at least the useful accurate matching of the numbers and the virtues, the playful investigation [of them], and [this] not idle exercise may convert [your] mind to it, so that you may have practice with the combination of numbers, and you may rejoice in the accumulation of virtues. In regard to what is to be acquired: if you win, [it is] not self-glorification, if you are conquered, you should not feel shame. For if you have gained less, [be] subject, if more, you should be kind to the one who is subject. To all those pursuing these virtues in Christ, cultivating [these] by their actions and habits, let there be grace and peace forever. Amen (see note 17).

During the play of the game, a player tries to acquire ownership of as many virtues as possible.

We assume that the four dice are placed in a cup and shaken out. In order to acquire a virtue four conditions must be met:

1. The number of vowels on each of the three cubical dice taken as an ordered triple identify a unique virtue, as found in Table 1;
2. the vowels appearing as pips on the exposed faces of the dice must include all those in the name of the virtue;
3. at least one of the consonants appearing on the bottom face of the tetrahedral die must be included in the name of the virtue;
4. the virtue must not have been previously acquired by another player.

For example, suppose a player has rolled \((1,2,3)\) in the form {A, IO, AEI}. This leads the player to find PAX on the game board  for which he has the vowel A. If the tetrahedron fell face down on either MNPR or on STXZ, the player would then own PAX – if it is still in play. We then suspect he would place a token in the spot on the game board to mark his acquisition.

Let's consider another example. To gain GAUDIUM, the player must roll a \((2,2,3)\) in which are found the vowels A, I, U and U. Now there are three ways to produce \((2,2,3)\): {EI, IO, AEI}, {EI, OU, UAE} or {IO, OU, OUA}. However, only two of these meet the vowel condition, the first of these not being viable. Of course, a consonant among G, D, and M must be cast on the bottom face of the tetrahedral die as well.

Play continues until all virtues have been acquired. Each player in turn is allowed to roll the dice and acquire another virtue.

Although not mentioned explicitly in the rules of the game, it seems that Wibold's own aesthetic made it desirable to him that a player acquire complementary virtues. Recall how he associated virtues together when their total point values summed to 21. Continuing with our example, if the player had acquired PAX with its value of 6, the player would also wish to acquire a virtue with value 15: CONFESSIO, SUSPIRATIO, or HILARITAS. This form of play would be natural for the players if Wibold had in mind a game board in the form of Table 6, as opposed to that of Table 5, in the section, Possible Game Boards, later in this article.

The cleric possessing the most virtues wins. If it should happen that a tie occurs, the cleric possessing KARITAS has his total incremented by one. This need not, however, determine a unique winner since the player with KARITAS might not be one of the tied players. If a tie cannot be broken, Wibold urged the players to rejoice in the outcome.

The outcome \((1,1,1)\) corresponding to KARITAS can be obtained in exactly one way: A, E, I. In this one instance, Wibold permitted a second cast of the dice in order to attempt to obtain a second A to satisfy the vowel condition so as to acquire this most important virtue.

A similar problem occurs with IUSTITIA, the outcome \((1,1,4)\), for which we need A, I, I, I, and U. There are three ways to obtain this pattern: {A, E, OUAE}, {A, I, IOUA}, and {E, I, EIOU}, none of which satisfy the condition required. Either Wibold made an error or he chose to ignore the initial I that here plays the role of a consonant just as he chose to ignore the consonant V. It may be verified that no other virtue has a similar difficulty in being able to satisfy the requisite conditions.

In order to appreciate the play of this game, an applet simulating the game is available here: Play the Game! The reader is invited to experiment with how Wibold's game parcels out the virtues.

The last paragraph of the passage above includes a simplified set of rules of the game presented by Wibold. Under these rules it suffices to examine the total of the three dice, the player acquiring all virtues corresponding to that sum. The game ought to proceed very quickly when using these simplified rules since a player can win up to six virtues on any one roll (see Table 2).

---

Notes

7.  The Latin actually has where the greater is six [quae major senarius].

8.  That is, \(1+2+\cdots+6=21\).

9.  By "the work," Wibold meant the game he was designing.

10. We mention also that such dice may be constructed to be either left- or right-handed as well.

11. Inspection of Table 1 will show that no virtue is spelled with the letter Q, which justifies Wibold's omission of this symbol from the labeling of the die. (As an aside, we note that one die in the modern word game Boggle is actually printed with the digraph QU rather than with a single letter.) Furthermore, the letter K, borrowed from the Greek alphabet, was used by Latin users only as the initial letter of a very small number of words and had long before Wibold's time fallen into disuse. It is interesting that Wibold chose the odd spelling KARITAS for the first in the list of virtues as this allowed the use of K in the game.

12. That is, the square-sided face of the cubical die.

13. On the tetrahedral die.

14. It seems the reference is to Table 1 or, more likely, to a game board.

15. The sixth hour is noon local time.

16. At this point the manuscript reads niati, not a known word, for which all editors make conjectures as to meaning. Colvener recommends aequitatem as supplying the most natural meaning. Indeed, all manuscripts are corrupt at this point and where the ellipsis appears later in the line.

17. The final Amen which appears in [2] is omitted in [4].

Was This Game Ever Played?

The game terminates when each virtue has been acquired by one of the players. It illustrates the so-called "Coupon Collector's Problem." A collector desires to acquire a complete set of coupons where these coupons are obtained by independent random trials. The collector seeks the expected number of trials required and, more generally, the probability distribution of the number of trials.

In Wibold's game, a given trial consists of the roll of the three cubical dice and a roll of the tetrahedral die. There are therefore \(6^3\times 4=216\times 4=864\) distinct equiprobable outcomes. However, a given virtue is acquired only if

• Its corresponding numeric values arrive on the upper faces of the cubical dice.
• Its vowels appear on the upper faces of the cubical dice.
• At least one of its consonants appears on the bottom face of the tetrahedral die.

We illustrate the computation of the probability of obtaining a virtue with several examples.

We saw that PAX corresponds to the outcome \((1,2,3)\). This outcome may be obtained in the following 6 ways in which the cubical dice are rolled:

A   IO   AEI	A   OU   AEI	E   EI   AEI
E   OU   OUA	I   EI   UAE	I   IO   OUA

All yield the requisite vowel A.

One face of the tetrahedral die contains P, another X. Therefore, the probability of obtaining PAX in a trial is \(\frac{6}{216}\times\frac{2}{4}=\frac{12}{864}\).

In the same manner, consider GAUDIUM. It corresponds to the outcome \((2,3,4)\) which may be obtained in the following 3 ways:

EI   IO   AEI

EI   OU   UAE

IO   OU   OUA

Only two outcomes contain an A, an I, and a U twice. Three faces of the tetrahedral die contain one of the consonants D, G, and M. Therefore, the probability of obtaining GAUDIUM in a trial is \(\frac{2}{216}\times\frac{3}{4}=\frac{6}{864}\).

The outcome \((1,1,1)\) corresponding to KARITAS contains the vowels A, E and I. A second roll is specially permitted to obtain the second requisite A. Regardless of choice of die, an A will appear on 4 of the faces. As for K, R, T, and S, the consonants occur on 3 of the faces of the tetrahedral die. Therefore, the probability of obtaining KARITAS in a trial is \(\frac{1}{216}\times\frac{4}{6}\times\frac{3}{4}=\frac{2}{864}\).

Proceeding in this manner, the probability associated with each virtue may be obtained. These probabilities are deduced from Table 3 by dividing each number in the table by 864. The probability that a roll yields no virtue at all (listed as NULL in the Table) is \(\frac{447}{864}\approx 0.52\). This spells trouble for the players of the game since slightly more than half the rolls do not advance the game.

Table 3. Number of outcomes yielding each virtue

Analysis of the Game

Figure 2 illustrates a realization of the game. Note the long periods where the game fails to advance. Repeated simulation of the game shows that the play resolves into three distinct parts: an initial segment, in which virtues are acquired quickly by the players until about 40 of the 56 have been distributed; a middle section during which acqusition of virtues slows down, until only two or three unacquired virtues remains; and a final very slow period of play, extending over hundreds, and even sometimes thousands, of rolls, until the final virtue has been acquired. The reader is invited to try out the applet simulator (see Play the Game!) to confirm this phenomenon for himself or herself.

Figure 2. A typical realization of Wibold's game

The expected number of rolls required to complete the game is given by the integral \[\int_0^\infty\left(1-\prod_{i=1}^m 1-e^{-p_it}\right)\,dt=1656.05\] where here \(m=57\) (the number of possible outcomes) and \(p_i\) is the probability associated with each virtue. For the derivation of this formula, see [10].

A simulation of the game conducted by one of the authors was repeated 10000 times in which the duration of the game was recorded. The relative frequency histogram displayed in Figure 3 shows the result. Here the sample mean of the number of rolls is 1656.126 and the sample standard deviation is 810.536. From these data, the estimated 95th percentile of total rolls is found to be 3222.

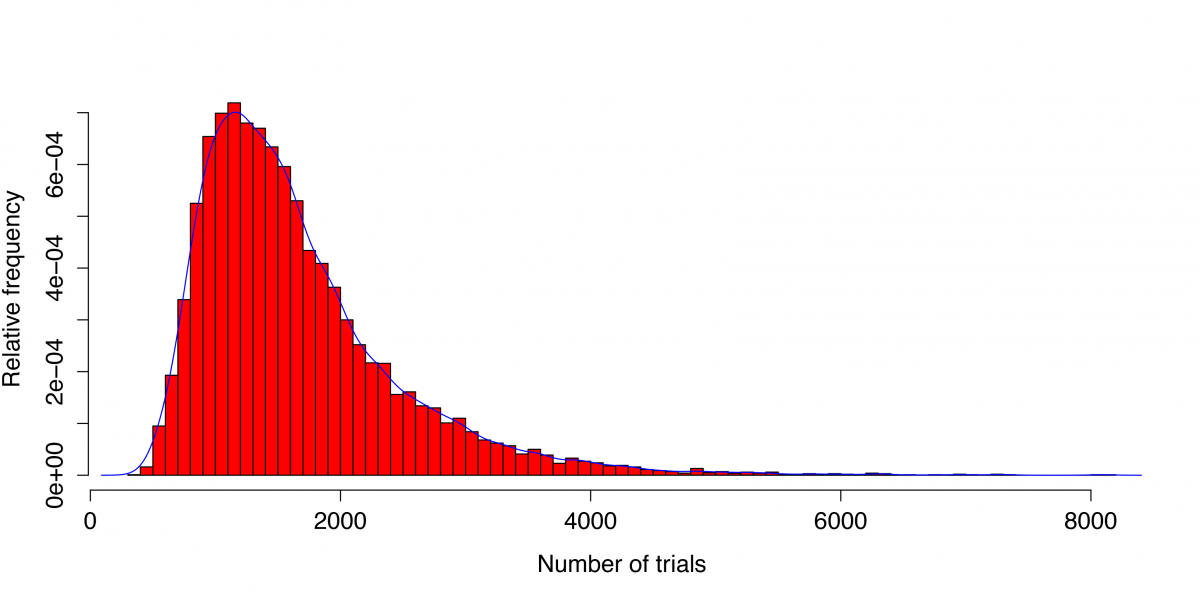
Figure 3. Empirical distribution of the duration of Wibold's game

Analysis of the Simplified Game

If the simplified game is played, a player receives all virtues having the same sum whenever that sum is cast. In the section on the enumeration of outcomes, we saw that there are 16 distinct sums ranging from 3 to 18 and we computed the number of ways that each can be obtained. These are shown in Table 4. The probability of each outcome is the number from the table divided by 216.

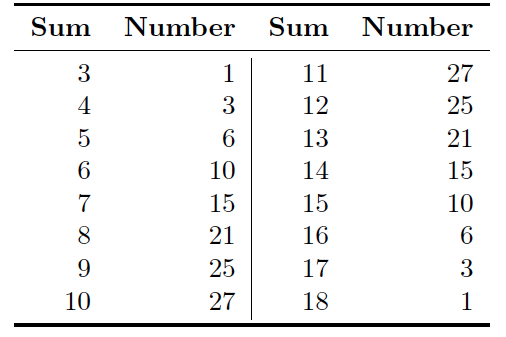
Table 4. Number of ways to obtain each sum

Figure 4 illustrates a realization of this abbreviated game. There is again a somewhat long period where the game fails to advance.

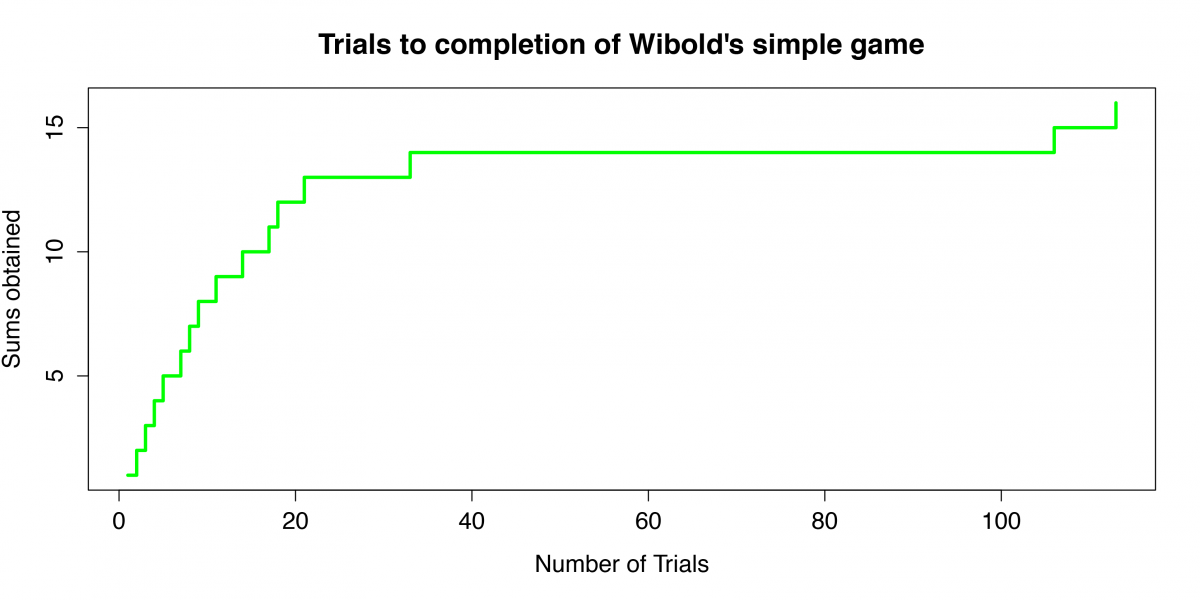
Figure 4. A typical realization of Wibold's simplified game

The expected number of trials is computed to be \[\int_0^\infty 1-\prod_{i=1}^m\left(1-e^{-p_it}\right)\,dt=338.45\] where here \(m=18\) and \(p_i\) is the probability associated with each sum.

A simulation of the simplified game was repeated 10000 times in which the duration of the game was recorded. The relative frequency histogram displayed in Figure 5 shows its result. Here the sample mean of the number of trials is 339.595 and sample standard deviation is 233.200. From these data, the estimated 95th percentile of total rolls is found to be 806.

Figure 5. Empirical distribution of the duration of Wibold's simplified game

If we assume that between 2 and 3 rolls can be cast and the corresponding virtue resolved during each minute of play, the duration of the game can be estimated.

This suggests that the game as Wibold described it was never actually played or, if it was, play was necessarily distributed over several sessions. It is difficult to imagine players devoting ten or more hours of continuous attention to this activity despite its moral benefits. As Figure 2, above, indicates, the bulk of the virtues are acquired within the first hundred rolls. Most of the rest arrive within 500 rolls. The last few however may require thousands more.

The simplified game, on the other hand, could well have been played. Even though the pattern of play is entirely similar to the longer game (Figure 4), its expected duration is one-fifth as long, requiring only a few hours of play.

The Author's Puzzle

At the end of the text, the author's name is disguised by means of the following verse. Colvener, editor of Balderic’s Chronicon [2], stated that this literary device was commonly used by medieval writers.

To solve the puzzle posed in the verse it is important to know that the Latin alphabet consists of only these 23 letters.

The name of the author is sought in these dactyls
If with numbers? Ten taken twice makes the first and the second,
And the eighth letter, and so with number nine
The third is thrown in, the fourth here to be the number two,
Four and ten the fifth, next finally number six
is read with the number eleven, twice two the seventh, as well as
The last in order limits in numbers thrice six.
To what has been brought together, the theoretical summit is dedicated
The virginity of the soul and the ten commandments, shine forth,
Which he who cares [for them] establishes for himself the delights of heaven.

This game advises the cleric to proceed to the gaming-table,
so that he may have the power to store up the names of the virtues.

The Game Board

Was Wibold's game truly a board game? It seems that it must necessarily have been the case. Aside from the conjecture that Wibold was attempting to draw clerics away from the game of Tables, to which he would have desired some similarity, stronger reasons in favor are that a surface is required for casting the dice, the spelling of the virtues must be displayed, and there must be a way to mark ownership of virtues once they are acquired. Any game board for Ludus Regularis would have to display this information before the players in order to serve these purposes. George Colvener and his colleague Boëtius Epo proposed three game boards [2].

One of these, designed for a simplified version of play, arranges the virtues in a circle with a spinner in the center. The randomizing device is the spinner; all the dice are abandoned. Employing this device ignores most of Wibold's instructions since each of the 56 virtues arrives with equal probability. This game board of Colvener and Epo, which was included as a foldout in [2], is reproduced here as Figure 6 [5].

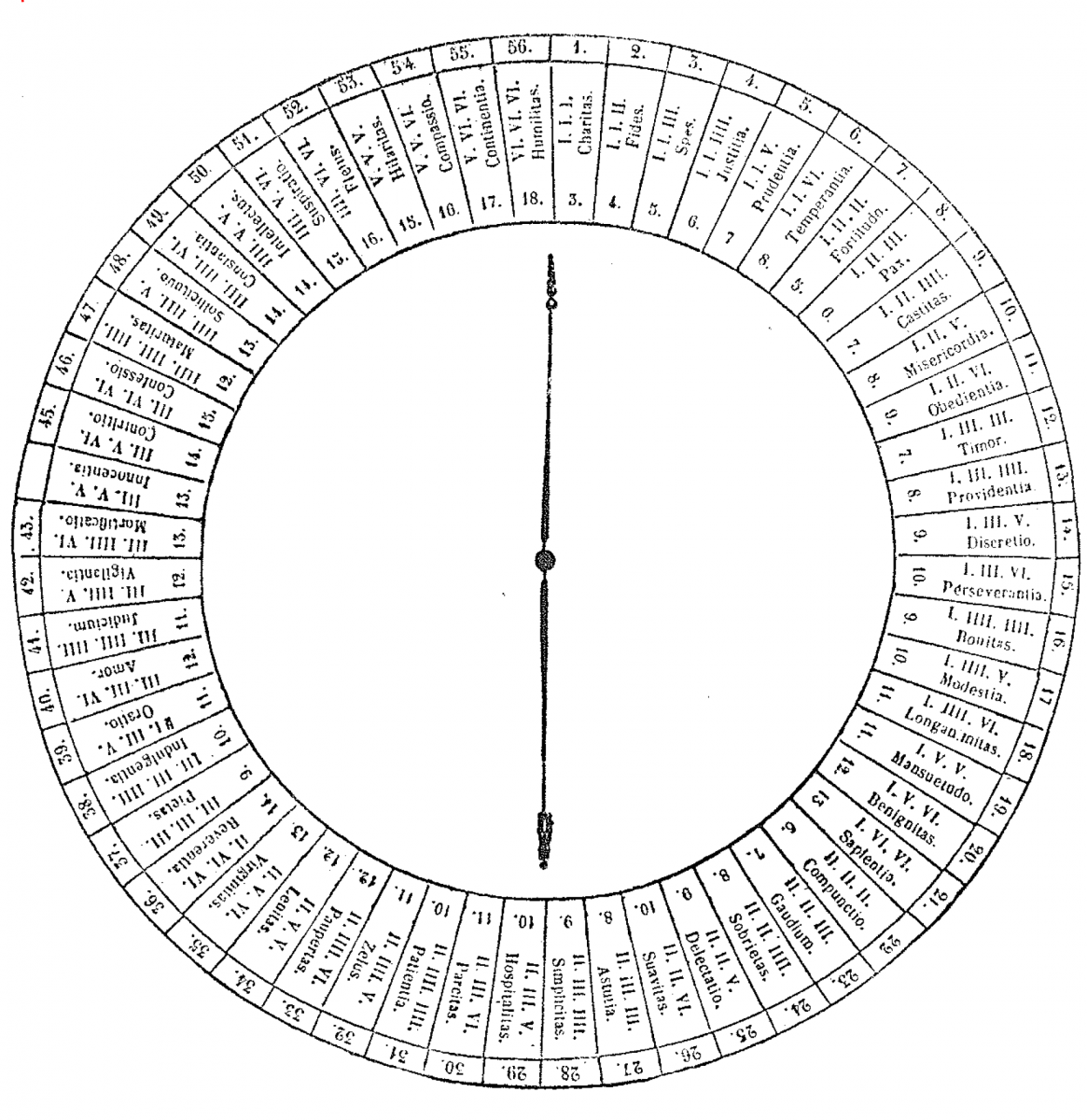
Figure 6. Colvener's proposed simplified game board (Courtesy of Xavier University Library)

The other two game boards proposed by Colvener and Epo [2] arrange the virtues in the same order as Table 1 within a rectangular border, much as on a modern Monopoly board. Although there are slight differences between the two, we offer the rectangular game board in Table 5 (see Possible Game Boards, next page), as an example of this type. Table 6 in Possible Game Boards (next page) is proposed by the authors as another alternative.

Relation to Rithmomachia

Is Ludus Regularis related to other games of its time? Le Glay stated in his notes on Wibold's text:

The game that he has invented has even some evident relationships with Rythmomachie, or philosophical game of Pythagoras, on which Claude Boissières has published a treatise, in octavo, 1556 [5].

The reference here is to a chess-like game known as the Philosopher's Game, or Rithmomachia – that is, (A)rithmomachia or “Battle of the Numbers" – from the Greek words arithmos and machē. Its origin was attributed to Pythagoras, as the name Rithmomachia also speaks to a Greek origin. The earliest written record we possess of it is a treatise by the monk Asilo of Würzburg dating from 1030. 

Rithmomachia is a game of strategy, whereas Wibold's game is one of pure chance. Rithmomachia is based on a theory of numbers somewhat sophisticated for that time; in Ludus regularis, the numbers are merely identifiers or, at most, the subject of arithmology. Moreover, Rithmomachia was not proscribed by authorities as was the game of Tables, due to the perceived moral hazard of dicing. For these reasons, we see little similarity between Rithmomachia and Ludus regularis with the following exception.

There is strong evidence that Rithmomachia was originally employed as a teaching tool to train its practitioners in the Nichomachian theory of numbers and that its popularity as a game came only centuries later. Similarly, Wibold promoted the playing of his game in order that the players “may have practice with the combination of numbers."

Thomas More described similar amusements in his Utopia of 1518. In Book II, Chapter IV we find a reference to Rithmomachia and a game similar to it involving a battle of virtues and vices.

Diceplaye, and suche other folish and pernicious games, they knowe not; but they use II games not muche unlike the chesse. The one is the battell of numbers, wherin one number stealethe awaye another. The other is wherin vices fyghte wyth vertues, as it were in battell array, or a set fyld. In the which game is verye properlye shewed bothe the striffe and discorde that vices haue amonge themselves, and agayne theire unitye and concorde againste vertues; and also what vices be repugnaunt to what virtues; and what powre and strenght they assaile them openlye; by what wieles and subteltye they assuate them secretelye; with what helpe and aide the vertues resiste, and ouercome the puissaunce of the vices; by what craft they frustate their purposes; and finally by what sleight or meanes the one getteth the victory. (See note 18.)

More's game mentioned above likewise bears no similarity to Wibold's. Wibold's game seems to be unique in its structure in that virtues (or properties) are acquired for the singular purpose of emulating them.

---

Note

18. Translated by Raphe Robynson, 1551 [14].

Possible Game Boards

Besides the circular game board in Figure 6, proposed for a simplified version of Ludus Regularis by Balderic's editor, George Colvener, in 1615 [2], we display two rectangular boards. First, we repeat Table 1, Wibold's Table of Virtues, with our English translation of virtues added, for easy reference.

Table 1. Wibold's Table of Virtues, with English translation of virtues added

A game board for Ludus regularis might have included the virtues in the order in which they appear in Table 1, arranged around the outside of a rectangular board, as in Table 5, below. A similar game board was proposed by Colvener [2].

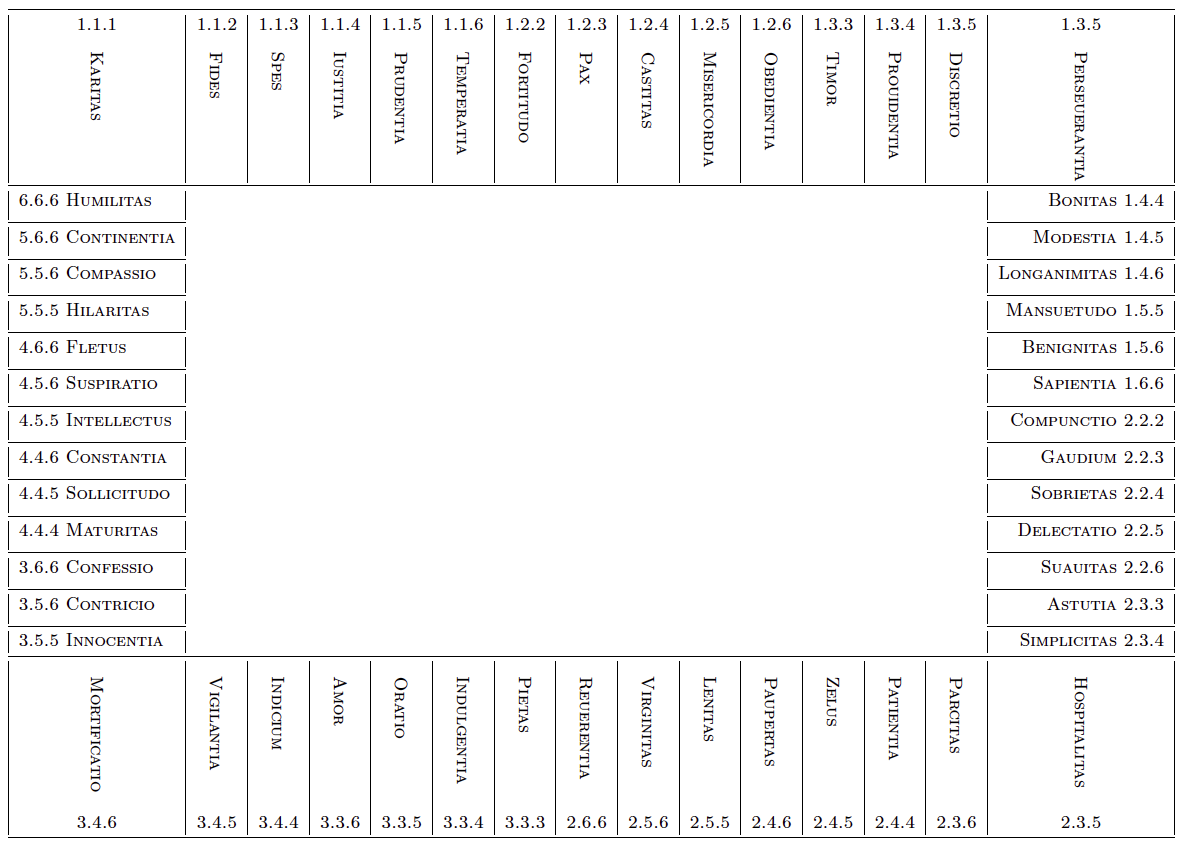
Table 5. Conjectural game board emphasizing order, modeled on a game board proposed by Colvener [2]

Table 6 shows a possible game board with the virtues ordered with respect to the sum of the dice, but with virtues paired with their complements, as discussed in the earlier section, "Game Play."

Table 6. An alternative game board emphasizing symmetries, proposed by the authors

The applet below, created by John Ensley, simulates play of Wilbold's Ludus Regularis (Canonical Game), a game of dice designed in 10th century Flanders by Wibold, Archdeacon of Noyon and later bishop of Cambrai and Arras. The game is played with four dice: three cubes, on which Latin vowels take the place of the dots we typically find on dice today; and a tetrahedron, on which are written 16 consonants, four to a side. Players alternate casting the dice, and with each roll attempt to collect one of 56 Virtues among those still available. The list of Virtues is provided at the bottom of the screen; each combination of the (exposed top) faces of the cubes corresponds to a unique one of the virtues (as in Table 1), and to acquire that virtue, the vowels appearing on the cubes must include all those in the name of the virtue. In addition, at least one of the consonants appearing on the (unseen bottom) face of the tetrahedron must be included in the name of the virtue as well.

A press of the ROLL button simulates a roll of the dice, corresponding to a player's turn, and the applet checks to see which virtue, if any, is acquired by the current player. The number of the roll is updated in the List of Virtues when that virtue is awarded to the player who has just rolled. If no virtue is awarded, the reason for the failure is given. To the right of the dice the history of the current game is updated displayed in graphical form: time (expressed as the number of dice rolls) on the horizontal axis, and the number of virtues acquired by the players on the vertical. Below this a progress bar also tallies the number of virtues distributed.

Clicking the AUTO button simulates the play of an entire game, and the RESET button allows play to start over.

Ready to play?

We repeat Table 1, Wibold's Table of Virtues, giving the dice roll required to acquire each virtue and with our English translation of virtues added, for easy reference.

Table 1. Wibold's Table of Virtues, with English translation of virtues added

References

[1] Wibold ou Wibald. Volume 50 (WA-WIM) of Biographie Universelle Ancienne et Moderne. L. G. Michaud, Paris, 1827.

[2] Balderic. Chronicon Cameracense et Atrebatense. George Colvener, editor. Ioannis Bogardi, 1615.

[3] Baudri ou Balderic. Volume 3 (BAM-BER) of Biographie Universelle Ancienne et Moderne. Madame C. Desplaces, Paris, 1854.

[4] Balderic. Gesta Episcoporum Cameracensium edente L. C. Bethmann, Volume VII of Monumenta Germaniæ Historica. Societatis Aperiendis Fontibus Rerum Gemanicarum Medii Aevi, Hanover, 1846.

[5] Wiboldi Cameracensis. Patrologia Latina Cursus Completus, Volume 134. Jacques-Paul Migne, editor. Paris, 1853.

[6] Corpus Juris Canonici. The Catholic Encyclopedia, Volume 4 (Cland­–Diocesan). The Universal Knowledge Foundation, Inc., New York, 1913.

[7] C. Chabaneau. Les sorts des Apôtres. Revue des langues romanes, 17–18:157–264, 1880.

[8] Dionysius Exiguus. Patrologia Latina Cursus Completus, Volume 67. Jacques-Paul Migne, editor. Paris, 1865.

[9] Will Durant. The Story of Civilization: Part IV. The age of faith. Simon and Schuster, 1950.

[10] Philippe Flajolet, Danièle Gardy, and Loöys Thirmonier. Birthday paradox, coupon collectors, caching algorithms and self-organizing search. Discrete Applied Mathematics, 39:207–229, 1992.

[11] Vincent Foster Hopper. Medieval Number Symbolism: Its sources, meaning, and influence on thought and expression. Dover Publications, Inc., 2000. Originally published by Columbia University Press, 1938.

[12] K. Kreith and Judith Kysh. The fourth way to sample k objects from a collection of n. The Mathematics Teacher, 81:14–149, 1988.

[13] André Le Glay. Chronique de Balderic. Levrault, J.-A. Mercklein, and Techéner, Paris, 1834.

[14] Thomas More and Raphe Robynson. Utopia. London, 1551. Second and revised edition, 1556. Numerous reprints.

[15] H. J. R. Murray. The mediæval games of tables. Medium ævum, X:57–69, 1941.

[16] Faverot and Petit. Chronique d'Arras et de Cambrai. Lemaitre, Valenciennes, 1836.

[17] Jorge-Nuno Silva. On mathematical games. BSHM Bulletin, 26:80–104, 2011.

Acknowledgment

The authors thank Cyril Whitaker, S.J. of Xavier University for his assistance in interpreting the Latin of the original, Doug Ensley and John Ensley for assistance with the game simulator, two anonymous referees for valuable suggestions that greatly improved this article, and the editor.

About the Authors

Richard Pulskamp is Professor of Mathematics and Computer Science at Xavier University in Cincinnati, Ohio. He received his PhD in mathematical statistics from the University of Cincinnati. His research interests currently lie in the history of probability and statistics.

Daniel E. Otero received his PhD from Penn State University in 1987 and, after a two-year post-doctoral position at Syracuse University, joined the faculty at Xavier University. He was elected Chair of the History of Mathematics SIGMAA in 2012, and is the 2014-2015 Chair of the MAA Ohio Section and its Archivist as well. With Daniel J. Curtin (Northern Kentucky University), he organizes the ORESME Reading Group, a seminar that meets twice a year in the Cincinnati area to read important historical mathematical texts.