Historical Activities for Calculus - Module 3: Optimization – Snell's Law and the Principle of Least Time
Snell's Law and the Principle of Least Time
Euclid's Law of Reflection, formulated around 300 BCE, tells us what happens when a beam of light is reflected off a mirror. The Dutch physicist Willebrord Snell (1580-1626) was interested in the phenomenon of refraction, which is the change in direction that occurs when a beam of light crosses a boundary from one medium (say air) into another (say water). He observed that when the light beam enters the denser medium at some point \(C\) on the line, its velocity decreases and its path bends toward the normal to the line at \(C.\)
Snell's experiments led him to the discovery of the following relationship, known as Snell's Law:
Figure 33. Snell's Law: \(\displaystyle{\frac{\sin \theta_1}{\sin \theta_2}={\rm constant}.}\)
Figure 34. Use this GeoGebra applet to investigate Snell's Law. You can drag \(C\) to determine the approximate location of the point that minimizes the time of travel along the path from \(A\) to \(C\) to \(B.\)
In 1637, Pierre de Fermat became interested in finding a theoretical derivation of Snell's Law. Recall that Heron had shown that if a light beam traveled from \(A\) to \(B\) by first reflecting off a line \({\mathcal L},\) the path taken was the one that would take the minimum time. Fermat reasoned that the same “least time” principle would govern that path from \(A\) to \(B\) across the boundary \({\mathcal L}.\)
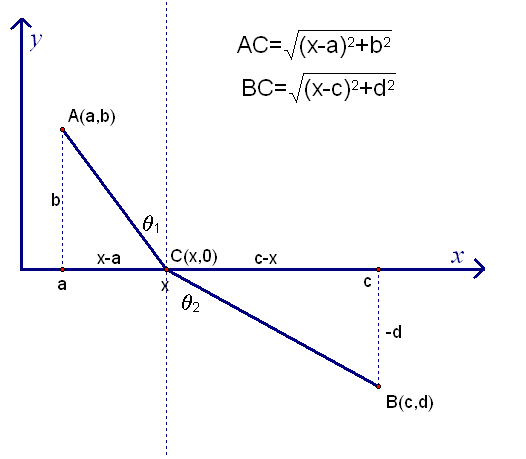
Fermat used the differential calculus (techniques which he himself developed by reasoning that the slope of a tangent line at a local maximum or minimum must be zero) to determine the quickest path. Suppose \(A=(a,b)\) lies above the \(x\)-axis and \(B=(c,d)\) lies below the \(x\)-axis, as in the picture below:
Figure 35. In modern terms and notation, Fermat wished to minimize the time of travel of a light beam along the path from \(A\) to \(C\) to \(B.\)
We wish to find the point \(C=(x,0)\) on the \(x\) axis that minimizes the time of travel of a light beam along the path \(A\) to \(C\) to \(B,\) assuming its velocity above the \(x\) axis is \(v_1,\) and its velocity below the \(x\) axis is \(v_2.\) Since \[\mbox{time}=\frac{\mbox{distance}}{\mbox{velocity}},\] the time of travel is
\[T(x)=\frac{\sqrt{(x-a)^2+b^2}}{v_1}+\frac{\sqrt{(x-c)^2+d^2}}{v_2}\]
If we take the derivative and set it equal to \(0,\) we have
\[\frac{\frac12\left[(x-a)^2+b^2\right]^{-1/2}\cdot 2(x-a)}{v_1}+\frac{\frac12\left[(x-c)^2+d^2\right]^{-1/2}\cdot 2(x-c)}{v_2}=0,\]
which can be rewritten as
\[\frac{x-a}{v_1\sqrt{(x-a)^2+b^2}}+\frac{x-c}{v_2\sqrt{(x-c)^2+d^2}}=0.\]
But since \[\sin\theta_1=\frac{x-a}{\sqrt{(x-a)^2+b^2}}\quad\quad{\rm and}\quad\quad\sin\theta_2=\frac{c-x}{\sqrt{(x-c)^2+d^2}},\] the above equation can be rewritten as
\[\frac{\sin\theta_1}{v_1}-\frac{\sin\theta_2}{v_2}=0\]
or, equivalently,
\[\frac{\sin\theta_1}{\sin\theta_2}=\frac{v_1}{v_2},\]
which is of course Snell's Law. But whereas Snell had conjectured his law based on observation, Fermat succeeded in giving a mathematical proof.
Fermat was led to investigate Snell's Law after reading a paper by René Descartes on the subject. Fermat thought Descartes' work did not make sense, and he could not understand how Descartes was able to arrive at the correct result using faulty and illogical arguments. Indeed, Fermat's criticisms could be interpreted as an accusation that Descartes, who made no mention of Snell in his work, had somehow gotten hold of Snell's experimental data, conjectured the correct law from the data, and then, working backwards, invented an argument that made little sense but led to the correct conclusion. Needless to say, Descartes did not take kindly to Fermat's accusations!
Exercises
Figure 36. Applet for Exercise 9, part a
Exercise 9.
(a) Use calculus (and a CAS if needed) to compute the value of the \(x\)-coordinate of the point \(C\) on the \(x\)-axis that minimizes the time of travel along \(A\) to \(C\) to \(B\) with \(A=(1,3),\) \(B=(4,-2),\) \(v_1=4\) units/sec, and \(v_2=5\) units/sec. Use the applet in Figure 36 to enter your solution to verify Snell's Law.
(b) Repeat part a with \(A=(-3,4),\) \(B=(2,-5),\) \(v_1=1\) unit/sec, and \(v_2=2\) units/sec.
(c) Use calculus and a CAS to find the coordinates of the point \(C\) on the curve \(y=-x^2,\) so that \(|AC|+|BC|\) is a minimum, where \(A=(0,4),\) and \(B=(5,-3).\) Illustrate your solution in GeoGebra, and measure the incidence and reflection angles to verify that they are equal. Your sketch should include the following:
- a plot of the curve \(f(x)=-x^2\)
- a plot of the two points \(A\) and \(B\)
- a plot of the point \(C\) that solves the problem, and
- a graph of the tangent line to the curve at \(C.\)