Historical Activities for Calculus - Solutions to Exercises
Module 1: Curve Drawing Then and Now
Exercise 1.
The equation is \[\sqrt{(x-c)^2+y^2}+\sqrt{(x+c)^2+y^2}=d.\] Solving for \(y\) we obtain \[y=\pm \frac{\sqrt{\left(-4 c^2+d^2\right) \left(d^2-4 x^2\right)}}{2 d}.\] The values of \(c\) and \(d\) for which the points \((0,\pm 5)\) and \((\pm 3,0)\) satisfy the equations(s) are \(c=4\) and \(d=10\). Substituting in these values and simplifying, the equations are




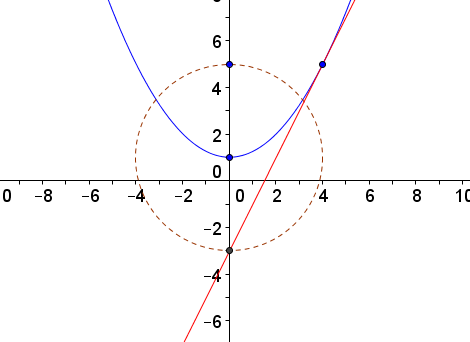









\[y=\pm\frac{3}{10}\sqrt{100-4x^2}.\]

Exercise 2.
We must have \(a+b=5\) and \(a-b=3\), so \(a=4\) and \(b=1\).

Exercise 3.
We must have \(\frac{a}{2}+b=5\) and \(\frac{a}{2}-b=3,\) so \(a=8\) and \(b=1\).

Exercise 4.
We must have \(a+b=5\) and \(a=3,\) so \(b=2\).

Module 2: Tangent Lines Then and Now
Exercise 5.
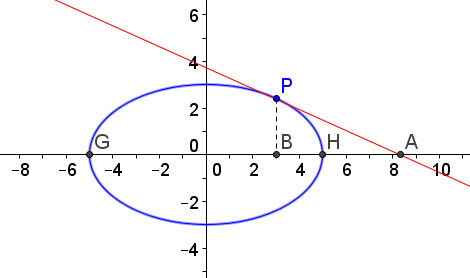
(a) Since the point \((4,5)\) is 4 units above the vertex, the \(y\)-intercept of the tangent line must be 4 units below the vertex, at \((0,-3)\).

(b) If the \(x\)-intercept \(A\) of the tangent line has coordinates \((x,0)\), then Apollonius' equation \[\frac{|AH|}{|AG|}=\frac{|BH|}{|BG|}\] becomes
\[\frac{x-5}{x+5}=\frac{2}{8}\]
Solving this for \(x\) we get \(x=\frac{25}{3}\) so the \(x\)-intercept is \((25/3,0)\).

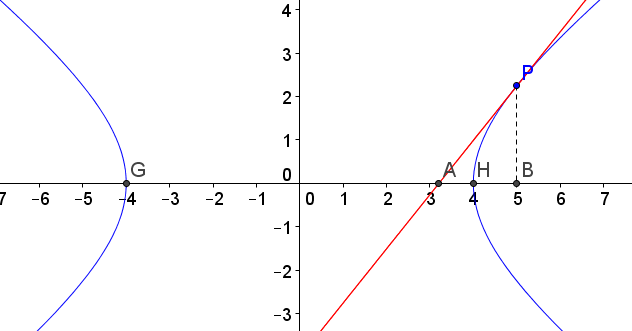
(c) If the \(x\)-intercept \(A\) of the tangent line has coordinates \((x,0)\), then Apollonius' equation \[\frac{|AH|}{|AG|}=\frac{|BH|}{|BG|}\] becomes
\[\frac{4-x}{x+4}=\frac{1}{9}\]
Solving this for \(x\) we get \(x=3.2\) so the \(x\) intercept is \((3.2,0)\).

Exercise 6.
(a) For the parabola, the tangent line is the angle bisector of \(\measuredangle FPB\):

(b) For the ellipse, the tangent is the angle bisector of \(\measuredangle {F_1^{\prime}}PF_2\) where \({F_1^{\prime}}\) is obtained by rotating \(F_1\) about \(P\) 180 degrees.

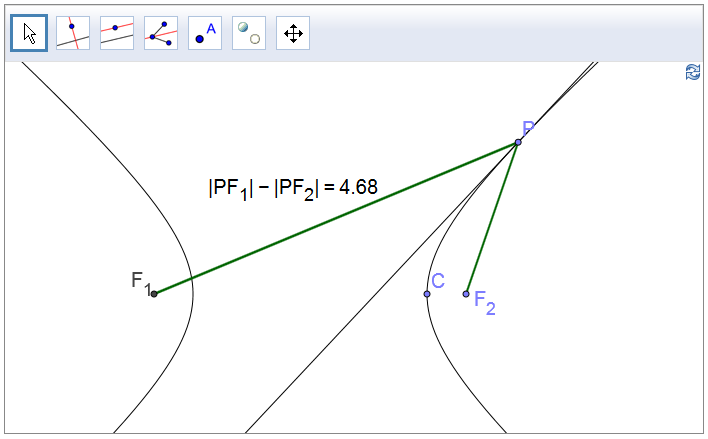
(c) For the hyperbola, the tangent line is the angle bisector of \(\measuredangle F_1PF_2\).

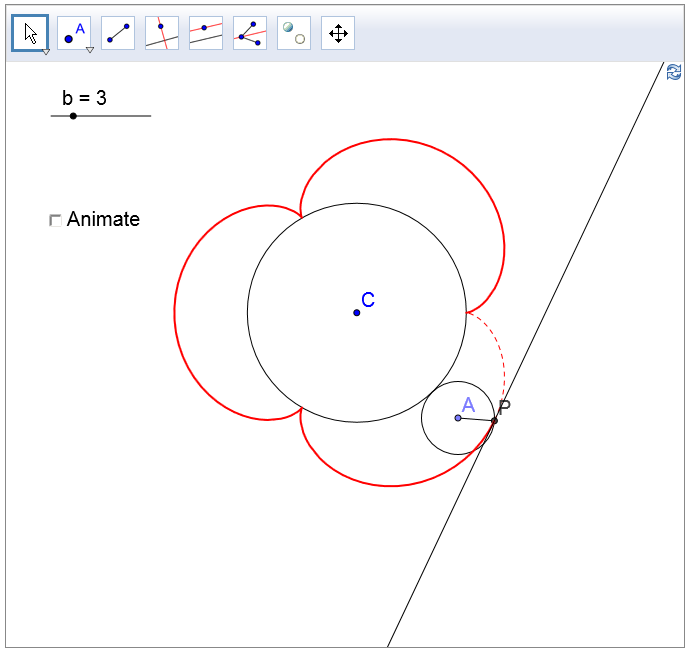
(d) There are two ways to approach the tangent line to the cycloid. You can think of \(P\) as being pulled by two forces, one parallel to \(EG\) as the position of the circle moves forward, and another perpendicular to the radius \(PC\) as \(P\) rotates about \(C\). So we construct a line through \(P\) parallel to \(EG\), and then another line through \(P\) perpendicular to \(PC\). The angle bisector of the angle between these two lines will then be the tangent.
Alternatively \(P\) is being rotated about \(A\), so we can just construct the perpendicular of \(AP\).

(e) For the epicycloid, there are two forces pulling on \(P\), one perpendicular to \(CA\), and one perpendicular to \(AB\). The tangent line is the angle bisector of the angle between these two lines.

Exercise 7.
(a) The center of the circle at which \(A\) and \(B\) merge is \((3,0)\). The slope of the radius of \(-1\), so the slope of the tangent line, which is perpendicular, is 1. Hence the equation of the tangent line is \(y-2=1(x-1)\) or \(y=x+1\).

(b) The center of the circle at which \(A\) and \(B\) merge is \((11,0)\). The slope of the radius of \(-3\), so the slope of the tangent line, which is perpendicular, is \({\frac13}\). Hence the equation of the tangent line is \(y-6={\frac13}(x-9)\) or \(y=\frac13x+3\).

Module 3: Optimization Problems Then and Now
Heron's “Shortest Distance" Problem
Exercise 8.
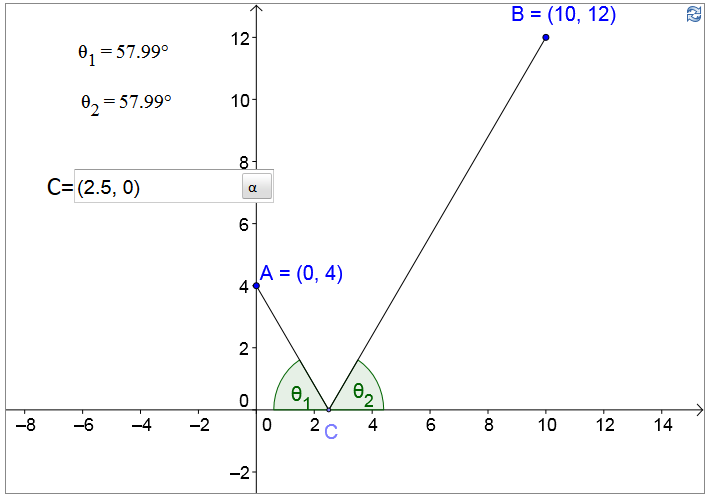
If \(C=(x,0)\), then we want to minimize
\[f(x)=|AC|+|CB|=\sqrt{(0-x)^2+(4-0)^2}+\sqrt{(10-x)^2+(12-0)^2}\] \[=\sqrt{x^2 - 20x + 244} + \sqrt{x^2 + 16}.\]
We use a CAS to compute the derivative:
\[f^{\prime}(x)=\frac{x-10}{\sqrt{144+(x-10)^2}}+\frac{x}{\sqrt{16+x^2}}\]
Then \(f^{\prime}(x)=0\Rightarrow x=\frac{5}{2}\). So the point \(C\) that minimizes \(|AC|+|CB|\) is \(C=\left(\frac52,0\right)\).

Snell's Law and the Principle of Least Time
Exercise 9.
(a) If \(C=(x,0)\), then we want to minimize
\[f(x)=\frac{|AC|}{v_1}+\frac{|BC|}{v_2}=\frac{\sqrt{(x-1)^2+9}}{4}+\frac{\sqrt{(x-4)^2+4}}{5}\]
We use a CAS to compute the derivative:
\[f^{\prime}(x)=\frac{x-1}{4\sqrt{9+(x-1)^2}}+\frac{x-4}{5\sqrt{4+(x-4)^2}}\]
Then \(f^{\prime}(x)=0\Rightarrow x=2.57363\).

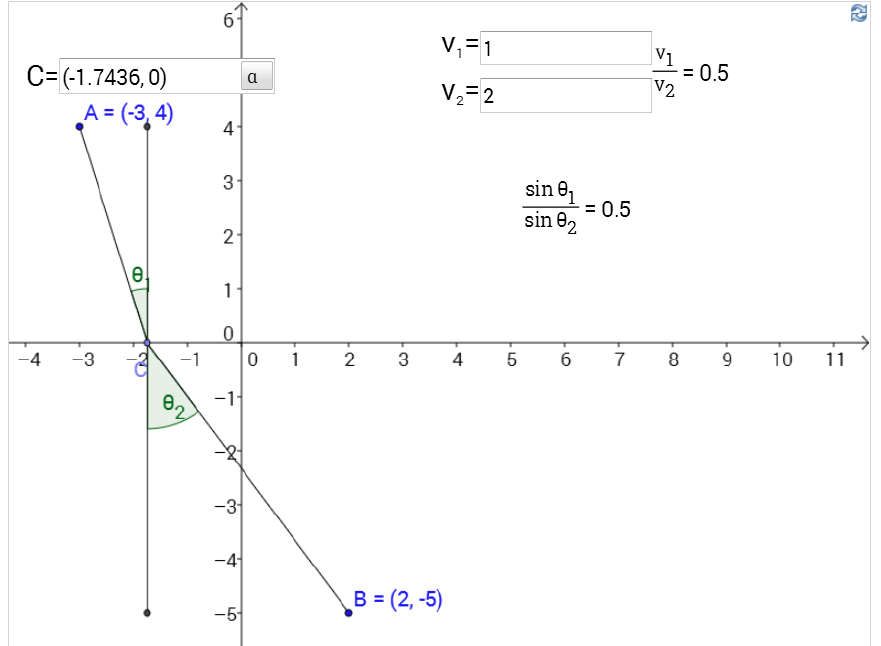
(b) We need to find the value of \(x\) that minimizes
\[f(x)=\frac{\sqrt{(x+3)^2+16}}{1}+\frac{\sqrt{(x-2)^2+25}}{2}\]
Taking a derivative, setting it equal to 0, and solving, we find the solution \(x=-1.743575120\).

(c) Let \(C=(x,-x^2)\). We need to find the value of \(x\) that minimizes \[f(x)=|AC|+|BC|=\sqrt{(0-x)^2+(4+x^2)^2}+\sqrt{(5-x)^2+(-3+x^2)^2}.\] Using a CAS to compute the derivative and solve \(f^{\prime}(x)=0\) numerically, we obtain the solution \(x=0.726582\).

L'Hôpital's Pulley Problem and the Principle of Least Potential Energy
Exercise 10.

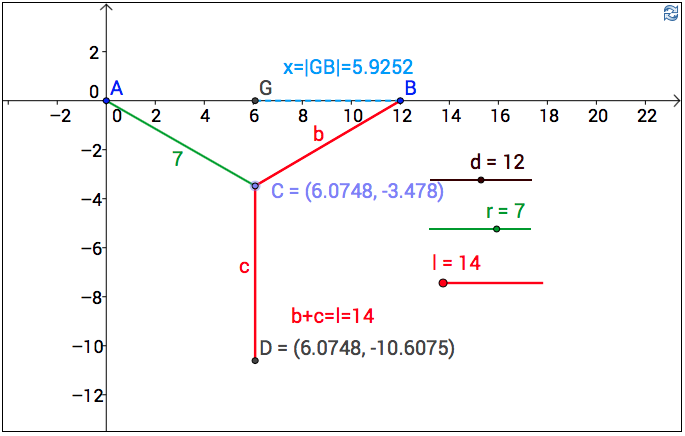
(a) \(|GA|=d-x\).
(b) \(|GC|=\sqrt{r^2-(d-x)^2}\).
(c) \(|BC|=\sqrt{x^2+r^2-(d-x)^2}\).
(d) \(|CD|=l-\sqrt{x^2+r^2-(d-x)^2}\).
(e) \(|GD|=\sqrt{r^2-(d-x)^2}+l-\sqrt{x^2+r^2-(d-x)^2}\).
(f) Using a CAS to differentiate the expression with respect to \(x\) and setting it equal to 0, we obtain the solutions
\[x=\frac{4d^2 - r^2}{4d} \pm \frac{|r|\sqrt{8d^2 + r^2}}{4d}.\]
(g) Plugging in \(d=12\), \(r=7\), and \(l=14\) above we obtain \(x=5.925247326\).
(h) Yes, the maximum value of \(|GD|\) is \(10.60747,\) and it occurs when \(x=|GB|=5.925247,\) which agrees (to four decimal places) with the answer obtained above.

Regiomontanus' Hanging Picture Problem
Exercise 11.
We need to find the value of \(x\) that maximizes \[\tan\theta=\frac{\frac{b}{x}-\frac{a}{x}}{1+\frac{b}{x}\cdot\frac{a}{x}}.\] Using a CAS to take a derivative and set it equal to zero, we obtain the solution \(x=\sqrt{ab}.\)
Exercise 12.
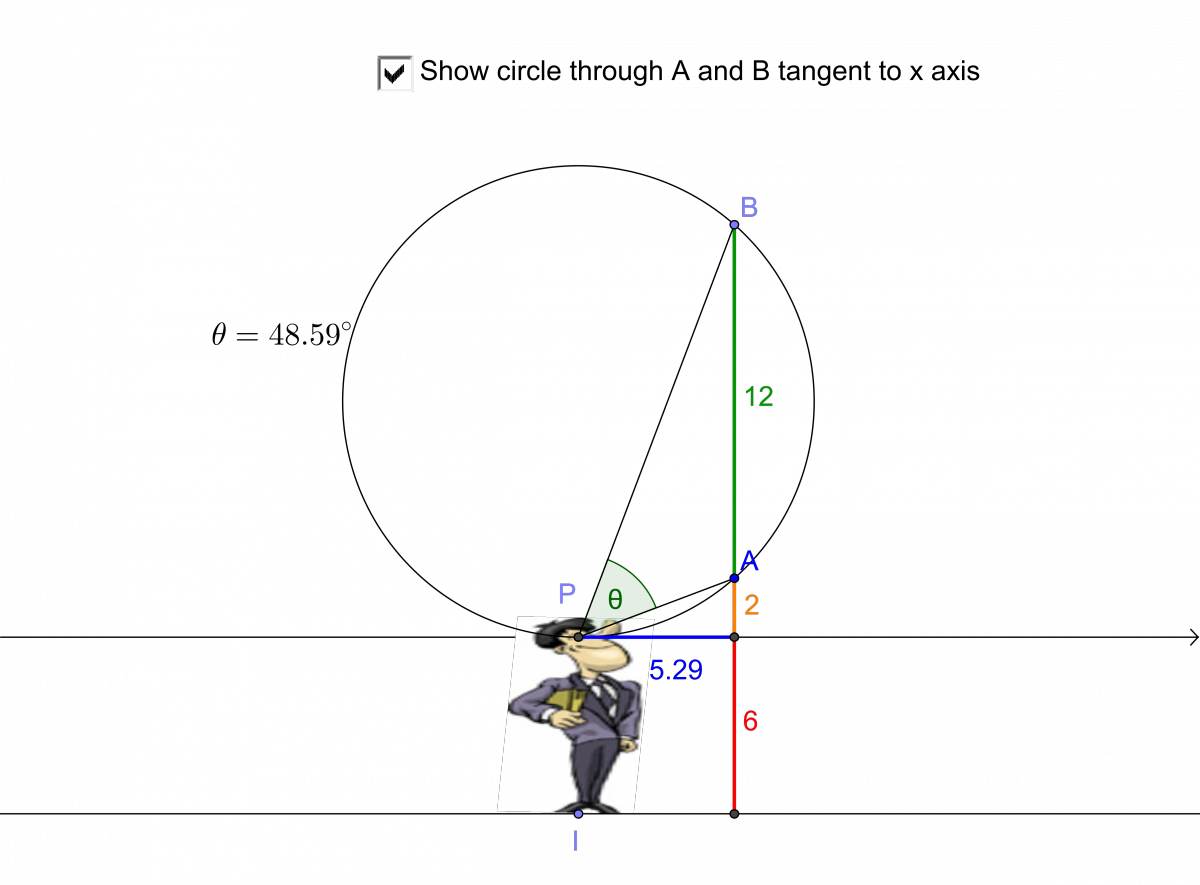
(a) The six-foot tall adult's eyes are two feet below the bottom of the painting. So \(a=2\) and \(b-a=12\). Hence \(b=14\) and so he should stand \(\sqrt{2\cdot 14}\approx5.291502622\) feet away from the painting.
The three-foot tall child's eyes are five feet below the bottom of the painting. So \(a=5\) and \(b-a=12\). Hence \(b=17\) and so he should stand \(\sqrt{5\cdot 17}\approx9.219544457\) feet away from the painting.
(b) Plugging \(a=2\), \(b=14\), and \(x=\sqrt{28}\) into the expression for \(\tan\theta\) we get \(\tan\theta=1.133893419,\) so \(\theta=0.8480620789\) radians. To convert to degrees we multiply by \(\frac{180\mbox{ deg}}{\pi\mbox{ radians}}\). Thus \[\theta=\frac{0.8480620789\cdot 180}{\pi}\approx 48.59037788\mbox{ degrees}.\]
Plugging \(a=5\), \(b=17\), and \(x=\sqrt{85}\) into the expression for \(\tan\theta\) we get \(\tan\theta=0.979067\), so \(\theta=0.774821\) radians. To convert to degrees we multiply by \(\frac{180\mbox{ deg}}{\pi\mbox{ radians}}\). Thus \[\theta=\frac{0.774821\cdot 180}{\pi}\approx 44.394\mbox{ degrees}.\]
c) For the 6-foot tall adult:

For the 3-foot tall child:

Galileo and the Brachistochrone Problem
Exercise 13.
(a) \(T(0,0,5,-5,0)=1.428571428\) seconds.
(b) \(T(0,0,1,-2,0)+T(1,-2,5,-5,V(0,0,1,-2,0))=1.333079013\) seconds.
(c) Taking a derivative, setting it equal to \(0\), and solving we find that \(x = 0.4491013975\). The \(y\)-value is \(-\sqrt{25-(x-5)^2}=-2.071067818\). So \(C=(0.4491013975,-2.071067818)\).
The time of descent along this path is
\[T(0,0,0.4491013975,-2.071067818,0)\] \[+\,T(0.4491013975,-2.071067818,5,-5,V(0,0,0.4491013975,-2.071067818,0))\]
\[=1.330475856{\mbox{ seconds}}.\]
This is less than \(1.428571428\), the time along the path \((0,0)\to (5,-5)\).
(d) Let \[v_1=V(0,0,0.4491013975,-2.071067818,0)=6.371258058{\mbox{ m/sec}},\] the terminal velocity along \((0,0)\to(0.4491013975,-2.071067818)\). We need to find \(x\) that minimizes
\[T(0.4491013975,-2.0710678181,x,-\sqrt{25-(x-5)^2},v_1)\]
\[+\,T(x,-\sqrt{25-(x-5)^2},5,-5,V(0.4491013975,-2.0710678181,x,-\sqrt{25-(x-5)^2},v_1)).\]
Taking a derivative and setting it equal to 0, we find \(x=2.043116864\). The corresponding \(y\)-coordinate is \(-\sqrt{25-(x-5)^2}=-4.031977445\), so \(D=(2.043116864,-4.031977445)\).
The terminal velocity as the object reaches point \(D\) is \[v_2=V(0.4491013975,-2.071067818,2.043116864,-4.031977445,6.371258047)=8.889699541{\mbox{ m/sec}}.\]
The total time along the path \((0,0)\to C\to D\to (5,-5)\) is \[T(0,0,0.4491013975,-2.0710678181,0)\]
\[+\,T(0.4491013975,-2.0710678181,2.043116864,-4.031977445,6.371258058)\]
\[+\,T(2.043116864,-4.031977445,5,-5,8.889699541)\] \[=1.327598538{\mbox{ seconds}}.\]
Exercise 14.
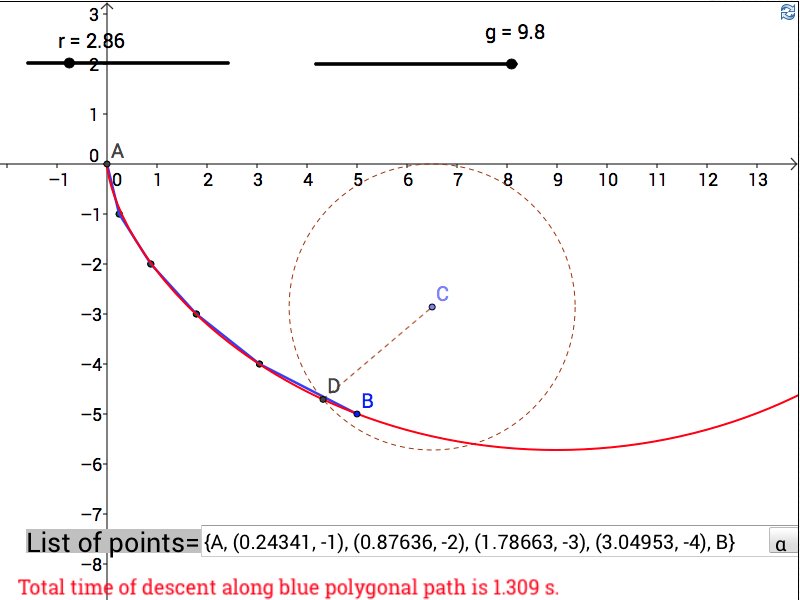
(a) We need to find the value of \(x\) that minimizes \[T(0,0,x,-1,0)+T(x,-1,5,-5,V(0,0,x,-1,0)).\] Taking the derivative and setting it equal to zero, the solution is \(x=0.2434120319\). So \(C=(0.2434120319,-1)\).
The terminal velocity as the object reaches point \(C\) is \[V(0,0,0.2434120319,-1,0)=4.427188724.\]
(b) We need to find the value of \(x\) that minimizes \[T(0.2434120319,-1,x,-2,4.427188724)+T(x,-2,5,-5,V(0.2434120319,-1,x,-2,4.427188724).\] Taking the derivative and setting it equal to zero, the solution is \(x=0.876358533\). So \(D=(0.876358533,-2)\).
The terminal velocity as the object reaches point \(D\) is \[V(0.2434120319,-1,0.876358533,-2,4.427188724)=6.260990337.\]
(c) We need to find the value of \(x\) that minimizes \[T(0.876358533,-2,x,-3,6.260990337)+T(x,-3,5,-5,V(0.876358533,-2,x,-3,6.260990337)).\] Taking the derivative and setting it equal to zero, the solution is \(x=1.786631272\). So \(E=(1.786631272,-3)\).
The terminal velocity as the object reaches point \(E\) is \[V(0.876358533,-2,-3,6.260990337)=7.668115805.\]
(d) We need to find the value of \(x\) that minimizes \[T(1.786631272,-3,x,-4,7.668115805)+T(x,-4,5,-5,V(1.786631272,-3,x,-4,7.668115805)).\] Taking the derivative and setting it equal to zero, the solution is \(x=3.049531298\). So \(F=(3.049531298,-4)\).
The terminal velocity as the object reaches point \(F\) is \[V(1.786631272,-3,3.049531298,-4,7.668115805)=8.854377448.\]
(e) The time of descent is
\[T(0, 0, 0.2434120319,-1, 0) + T(0.2434120319,-1, 0.876358533,-2, 4.427188724)\]
\[+\,T(0.876358533,-2, 1.786631272,-3, 7.668115805) + T(1.786631272,-3, 3.049531298,-4, 8.854377448)\]
\[+\,T(3.049531298,-4, 5, -5, 8.854377448)\] \[=1.309306399\mbox{ seconds}.\]
This is less than \(1.327598538,\) the time along the polygonal path from the previous exercise.
(f) \(r\approx 2.86\)

