Historical documents are widely recognized as useful components of mathematics teaching, but historical objects are not often used for instruction. Availability is certainly part of the reason for the disparity, as procuring physical artifacts can be difficult and expensive, while museum collections of mathematical and scientific instruments have usually been unavailable to the general public. Museums typically own many more objects than they can display at one time, while storage locations for objects may not be easily accessible even to those researchers who are able to make arrangements with curators to see the collections they manage. However, numerous digitization projects around the world have made it possible for teachers and professors to bring virtual versions of objects into their classrooms. Museums and other repositories can now share photographs as well as information about the history and use of individual objects that far exceeds the amount of text that is feasible in an on-site exhibit. This article highlights the online collections of mathematical and related objects of the Smithsonian Institution, particularly those of the National Museum of American History (NMAH). Other online resources and suggestions for utilizing online museum collections in the mathematics classroom are also described.

Peggy A. Kidwell, mathematics curator at the National Museum of American History, demonstrates a salesman's model of an IBM System 360 computer from about 1965 to Brian Gellasch in May 2013. Personal photo.

Since 2012, the Smithsonian's National Museum of American History (NMAH) has organized online collections records into “object groups.” The term is a little obscure, but the underlying idea is that objects that have some sort of common bond are cataloged thoroughly and brought together on one website, as if they were in an encyclopedia of apparatus relevant to American history. NMAH staff members and, sometimes, volunteers supply overview text for each category of object to help visitors understand what they are seeing, and they additionally provide resources for further information. Some of the groups are thematic, such as Arithmetic Teaching Apparatus or Women Mathematicians whose lives are documented in the Museum's collections. Most of the object groups, though, focus on one type of artifact. This characteristic makes them particularly appealing to those museum visitors, such as collectors and other enthusiasts, who care about only one thing but care about that one thing very much. The object groups can also help users identify historical items they have found in their own homes, workplaces, or academic institutions. At the same time, the online format allows Museum staff to point out commonalties between categories of objects, such as Gunter scales, English-style sectors, and slide rules, all of which are used to perform calculations with logarithmic scales.

A screen shot of the home page for NMAH's object groups, preserved October 8, 2014, shows two of the mathematics groups: Kinematic Models and Women Mathematicians.

A wide variety of objects from NMAH's vast collections are included, with mathematical items especially well represented. At least one “treasure” from most of the mathematics object groups is also highlighted in Convergence:

• Abaci & Numeral Frames – Modern Chinese Abacus
• Adders – Troncet Arithmographe Owned by Daniel Draper
• Adding Machines – Jean Lepine’s Stylus-Operated Adding Machine
• Adding Machines – Thomas Hill's Patent Model for a Key-Driven Adding Machine
• Arithmetic Teaching Apparatus – Add-A-Count Scale for Teaching Arithmetic
• Bookkeeping Machines – National Class 3000 Bookkeeping Machine
• Calculating Machines – Frederick A. P. Barnard's Calculating Machine
• Cash & Credit Registers – Model Cash Register Designed by the Ritty Brothers
• Charter Members of MAA – Geometric Model by Harry Wheeler
• Counters – Moffett Register for Recording Alcohol Sales
• Dividers & Drawing Compasses – Maurice Kidjel's Ratio Cali-Pro
• Electronic Calculators (Desktop) – Wang Loci-2 Programmable Calculator
• Electronic Calculators (Handheld) – Hewlett-Packard HP28S from the AMS Centennial Meeting
• Ellipsographs – Keuffel & Esser Trammel Ellipsograph
• Flowcharting Templates – RCA Flowcharting Template
• ​Geometric Models – Dissected Rhombic Dodecahedron by A. Harry Wheeler
• Geometric Models – Elongated Pentagonal Pyramid
• Geometric Models – Jullien Models for Descriptive Geometry
• Geometric Models – Paper Model of Elliptic Paraboloid by Brill
• Geometric Models – Thermodynamic Surface by Richard P. Baker
• Geometric Models – Transformable Plane Dissections by A. Harry Wheeler
• Geometric Models – Wire Frame for Soap Film Minimal Surface by Brill
• Kinematic Models – Hypotrochoid Kinematic Model by M. Schilling
• Mathematical Charts & Tables – Number Line Owned by Andrew Gleason
• Mathematical Paintings – Crockett Johnson's Mathematical Paintings
• Mechanical Integrators and Differential Analyzers – Product Integraph by Vannevar Bush and Colleagues
• Metric System Demonstration Apparatus – Demonstration Metric Grain Measures
• Parallel Rules – Captain Field's Improved Parallel Rule
• Pens & Pencils – Rubik's Cube Museum Promotional Pen
• Planimeters – Polar Planimeter Invented by Jacob Amsler
• Protractors – Japanese Protractor for the 1876 World's Fair
• Punch Cards – Factor Stencil Punch Cards
• Scale Rules – Nels Ockerlund's Patent Model for a Combination Ruler
• Sectors – Sector from Jesse Ramsden's Workshop
• Sets of Drawing Instruments – Early Modern Drawing Instruments
• Slide Rules – Raymond Clare Archibald's Slide Rule
• Spherometers – Grunow Spherometer
• Tabulating Equipment – Statistical Tabulator of Benjamin Wood
• Teaching Machines & Mechanical Learning – B. F. Skinner’s Arithmetic Teaching Machine
• Triangles & Squares – Blackboard-Sized Triangles
• Trigonometry in the Plane – Trigonometer for Use with World War II Artillery
• Trigonometry on the Sphere – Model of Spherical Triangle by A. Harry Wheeler
• Women in Mathematics – Objects Related to Women Mathematicians
• Women Teaching & Learning Mathematics in the United States – Boole Senior Blocks Designed by Edith Dummer Mintzer

Each object group has a home page with a general overview. Unless the group is very small (a dozen or so items), a Contents box on the right side provides links to pages for different forms of the object. For instance, the Adding Machines are divided into those that were operated with a stylus, those that had full keyboards (by Felt & Tarrant, by Burroughs, and by other manufacturers), those that had ten keys or fewer, and those that were finger-operated. While most of the groups provide descriptions of about 60 objects, some of the groups are very large, with hundreds of instruments; examples include Adding Machines, Calculating Machines, and Slide Rules. The Slide Rules group is unusual in that it is indexed several different ways to make it easier to locate specific models of slide rules: by shape or form, by manufacturer, by the materials from which they were made, and by purpose. Most of the groups show tools of engineering, business, and education, but the Mathematical Paintings of Crockett Johnson are unique for representing geometrical principles in which Johnson found aesthetic value. Each group has a page of Resources for further reading.

The home page for the Protractors Object Group, preserved October 27, 2014, shows several different functions for protractors in the Contents listing.

Clicking on the name of an object at the bottom of a section page leads to the online catalog record for that object. These are typically thorough descriptions that include references. Clicking on the thumbnail image next to the description calls up a larger version of the image, with tools for zooming in and out from the image and a link to a higher-quality image suitable for downloading to use for lecture illustrations and the like. Note that the Smithsonian negative number is in the URL for this image, as well as in the file name of the downloaded file. Since the Smithsonian Institution is partially funded by the U.S. government, its online materials are in the public domain and generally there are no copyright restrictions on digitized images used for noncommercial purposes. Nonetheless, users should include a credit line when using images in presentations and publications and provide two copies of published works to the Smithsonian Institution Libraries. Additional photographs may appear at the bottom of the object's catalog record page. The pages for individual objects mimic social media in that the Museum also allows visitors to write comments at the bottom of the page; comments and questions are passed on to the appropriate curator.

Object groups continue to be added to the NMAH website, so readers should make it a habit to visit the site (http://americanhistory.si.edu/collections/object-groups) to check for updates.

The home page for the Smithsonian's Collections Search Center on October 27, 2014, with “adding machines” entered into the search box.

The National Museum of American History (NMAH) website may also be searched by subject, with various filters suggested in a text box on the right side of the page, or for types of objects, or for individual items. Additionally, all of these objects are included in a parent database that covers the entire Smithsonian Institution of 19 museums and galleries and 20 libraries. For instance, when searching the term “slide rules,” after a few pages of scrolling through the approximately 230 objects that can also be viewed in the NMAH Slide Rules Object Group, the user encounters the slide rules that are housed at the National Air & Space Museum. To use the Collections Search Center, enter a keyword, such as a type of object, in the box and click on “Search.” If cataloguing and uploading has been completed for the desired mathematical instrument or computer, the search box will auto-fill the term for you. Users can limit searches to museum objects or library materials, but note that objects from NMAH are not included in the Science & Technology category. Similarly, the Browse by Category feature does not contain any of the mathematics records, and Items on Exhibit excludes NMAH.

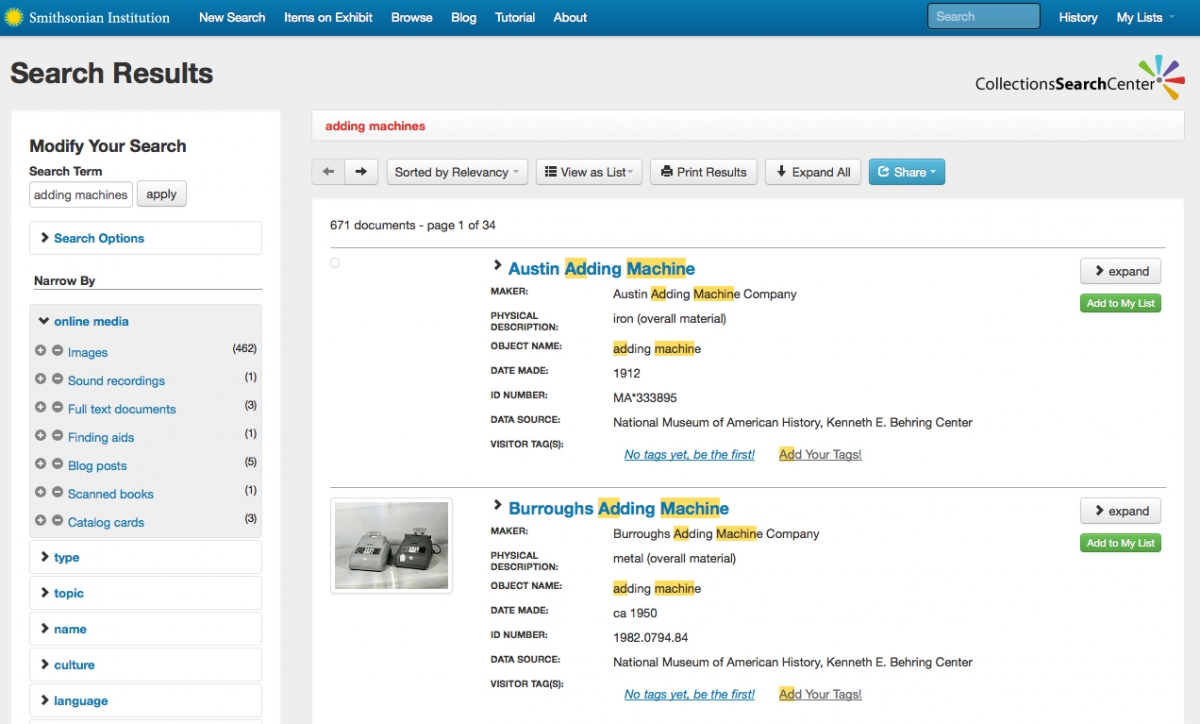
The top results from our “adding machines” search.

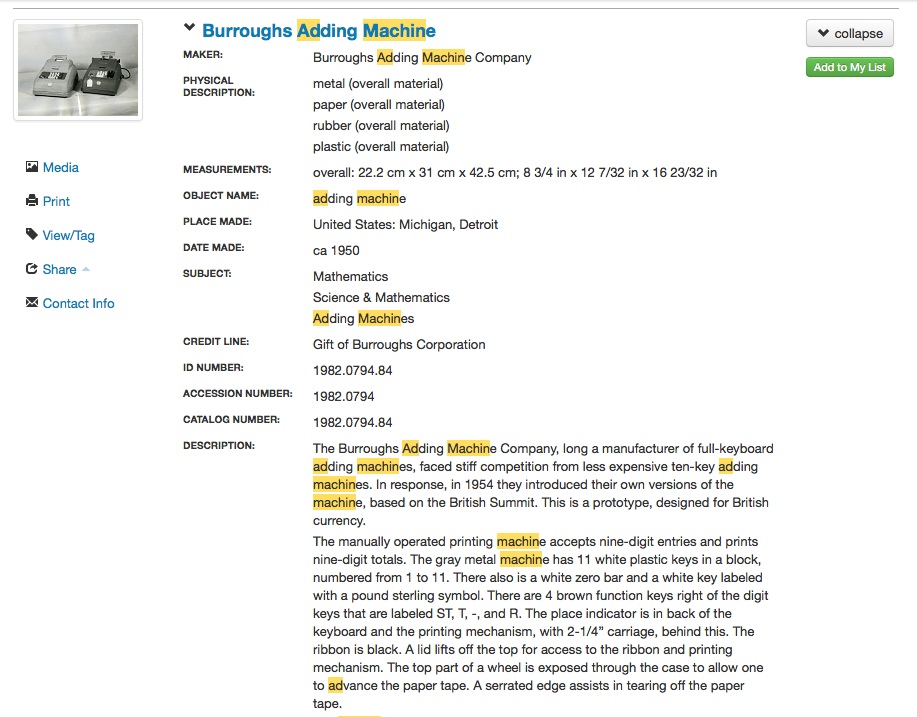
The expanded view of the catalog record for this Burroughs adding machine.

The Collections Search Center website also has a blog that features individual items in the Smithsonian collections, an About page that provides some history of the Smithsonian's experience with online collections databases, and a Tutorial page that covers basic searching techniques. Additionally, NMAH maintains a blog, O Say Can You See, which occasionally features items from the mathematics collections. See, for instance, the Convergence article, “Celebrating a Mathematical Miracle: Logarithms Turn 400,” which was reprinted from this blog.

Some of the most user-friendly and comprehensive collections of digitized mathematical and scientific instruments include:

• The British Museum, London, http://www.britishmuseum.org/research/search_the_collection_database.aspx
• Department of the History of Science, Harvard University, Waywiser, http://dssmhi1.fas.harvard.edu/emuseumdev/code/eMuseum.asp?lang=EN
• International Slide Rule Museum, edited by Mike Konshak, http://sliderulemuseum.com/
• MIT Museum Collections, http://webmuseum.mit.edu/
• Museum of the History of Science, Oxford, http://www.mhs.ox.ac.uk/collections/search/
• Museum of HP Calculators, http://www.hpmuseum.org/search.htm
• National Maritime Museum, Greenwich, http://www.collections.rmg.co.uk/
• National Museum of Australia, Canberra, http://www.nma.gov.au/collections-search/
• Powerhouse Museum, Sydney, Australia, http://www.powerhousemuseum.com/collection/database/menu.php
• The Science Museum, Kensington, http://www.sciencemuseum.org.uk/onlinestuff/museum_objects/mathematics.aspx
• University of Toronto Scientific Instruments Collection, L. E. Jones Collection. https://utsic.escalator.utoronto.ca/home/blog/category/collections/l-e-jones/

Classroom Application #1: Research Projects

Each of the National Museum of American History (NMAH) Object Group sites has a Resources page with a bibliography (often annotated) of primary and secondary sources related to the object. The catalog descriptions of individual objects are designed to be understood by a range of audiences, including researchers, teachers and students, and the general public. Almost all of these records end with a list of sources for the object, its maker, or its previous owner (if known). As NMAH physical sciences curator Debby Warner puts it, the entries should provide enough information so that visitors understand what they are seeing and lack enough information so that they are inspired to learn more on their own. Thus, instructors can assign papers that report on the history of a category of objects, or they can ask students to find out more about particular objects. Additionally, students and professors can search the storerooms of their institutions for objects such as geometric models, slide rules, or blackboard drawing instruments. Even if the actual teaching tools have not survived, photographs may be found in college or university archives. Information learned about items owned by one's institution may be shared with a campus newspaper or alumni magazine. Small exhibits may be mounted in a department or by collaborating with a university museum; one guide to preparing a display is “Exhibiting Mathematical Instruments: Making Sense of Your Department's Material Culture,” by Peggy Aldrich Kidwell and Amy Ackerberg-Hastings, in Hands on History: A Resource for Teaching Mathematics, ed. Amy Shell-Gellasch (Washington, DC, 2007), 163–174.

Beyond the sources that NMAH staff and volunteers have already identified, additional data can be unearthed by creative use of search engines, visits to the Ancestry and Find A Grave websites, perusals of online newspapers, and searches of digitized collections of 19th- and 20th-century books, such as Google Books and the Internet Archive. Mathematical instruments were discussed in instruction manuals, textbooks on practical mathematics and engineering, periodicals, patent records, and even in fiction—for example, Maria Edgeworth's short story, “Lame Jervas” (completed before 1804), mentioned the mathematical instrument workshop of Jesse Ramsden in chapter 3 and cited diplomat and travel writer Sir John Barrow's A Description of Pocket and Magazine Cases of Drawing Instruments: in which is explained the use of each instrument, and particularly of the sector and plain scale, Gunter's scale, &c. (ca 1792) in chapter 4. Alex Kasman's Mathematical Fiction site can be worth checking.

With help from history teachers and librarians, mathematics instructors can also work with students on connecting the objects to other historical developments. For instance, while each object group is fairly comprehensive in presenting the chronological history of the type(s) of instruments included in the group, almost every group is especially well-documented for the decades between about 1890 and 1920. This is probably partly because American manufacturing and business had its “take-off” period during the Second Industrial Revolution: American makers were able to produce their own instruments in large quantities, and communication and transportation technologies enabled makers to market their wares across the nation and sometimes even internationally. Particularly with drawing instruments, however, engineers and draftsmen often continued to believe that Germany and Switzerland produced the highest quality items, so imports are found in the collection through the middle of the 20th century. Meanwhile, this period was also the take-off of the professionalization of engineering and the trades, so there was a growing audience to buy mathematical instruments. In many ways, it is easier to document the history of instruments from this period than those that were made earlier or later, since manufacturers' catalogs were printed for mass distribution. These catalogs are now out of copyright, so some that may not be on hand in university libraries have been digitized for GoogleBooks or the HathiTrust.

Other stories that can be told by poring through the NMAH mathematics collections include those of the manufacturers Keuffel & Esser, Pickett, Felsenthal, Dietzgen, and Safe-T; the Empire of Japan Department of Education’s exhibit in Philadelphia at the Centennial Exposition (the 1876 World's Fair); patent models submitted by American inventors; objects collected by Leslie Leland Locke (1875–1943), a mathematics professor, avid collector of calculating machines, and charter member of the MAA; and instruments that may have been used by the Draper family of New York City, which was prominent in meteorology and astronomy in the late 19th century. The object groups reveal the diversity of the NMAH mathematical collections and thus the diversity of mathematical activities in American history.

Classroom Application #2: Demonstrations of Physical Objects

The object groups can also be used to stimulate ideas about vintage or historic mathematical instruments that are available to you, which can then be demonstrated in class. Perhaps friends or family members of a certain age have held on to the slide rules and sets of drawing instruments they used in undergraduate engineering and science classes. Perhaps you have older models of scientific or graphing calculators stashed in a drawer. Perhaps your institution has a case of 19th- or early-20th-century geometric models or calculating instruments. Perhaps a local historical society or house museum collects books and objects related to mathematics education. Some of the works listed on each group’s Resources page provide instructions for guiding students through making various types of mathematical instruments.

Vintage slide rules and drawing instruments from personal collections were shared with a pre-kindergarten class at the Smithsonian Early Enrichment Center in February 2013. The class was studying the teamwork between construction workers and architects, so a few minutes were spent talking about how architects used to use T-squares, triangles, protractors, and slide rules to make precise drawings that construction workers used to make buildings. Photo by Carrie Heflin.

Mostly, though, the children were allowed to handle the objects. They washed their hands first but wore white cotton gloves that protect historic instruments from the oils on human hands only for fun, since these objects were not rare or especially fragile. While the children did not comprehend how slide rules worked as calculating instruments, they enjoyed using them like rulers to measure the classroom. They also discovered that slide rules make excellent swords, signaling the time to end the classroom visit. Photo by Carrie Heflin.

The instruments were also passed around an assembly of the middle school classes at the Mustard Seed School in Hoboken, NJ, in February 2013. (A clear plastic protractor is in Amy Ackerberg-Hastings's left hand.) Photo courtesy of Gary Lawrence.

Classroom Application #3: Art and Geometrical Constructibility

Crockett Johnson's mathematical paintings can be an excellent way to show students intersections between mathematics and art while exploring the principles of geometry. Stephanie Cawthorne of Trevecca Nazarene University used a version of her article, “Cubes, Conic Sections, and Crockett Johnson," to introduce constructibility to undergraduates studying Euclidean and non-Euclidean Geometry.

A study of the constructibility constraints of a compass and unmarked straightedge, discussed in “Three Greek Problems” and “Constructions in Euclid’s Elements,” can be enhanced by having students construct various segments of length a + b, a – b, a·b, a/b and \(\sqrt{a}\). Crockett Johnson’s painting Square Roots to Sixteen provides a nice visualization of the constructibility of \(\sqrt{a}\). When considering the inconstructibility of some of the ancient problems, Crockett Johnson's paintings suggest examples of other means of construction. For instance, Problem of Delos (Menaechmus) shows how Johnson portrayed a conic section solution to doubling a cube, and Construction of the Heptagon gives an original Neusis construction of a regular heptagon. Students are often drawn in by Crockett Johnson's creative interpretations of ancient constructions, along with his fascinating original constructions for well-known problems.

At the other end of the educational spectrum, Amy Ackerberg-Hastings has used Square Roots to Sixteen and Squares of a 3–4–5 Triangle in Scalene Perspective with pre-K, kindergarten, and 1st-grade children to discuss shapes, colors, and patterns. After the kids in each class identified the squares and triangles in the second painting's representation of the Pythagorean Theorem, they worked together with the adults to count the squares and figure out that the 9 + 16 squares on the two legs of the right triangle were the same as the 25 squares along the hypotenuse. While it is unlikely the children will remember that relationship when they next encounter the preliminaries of analytic geometry, they did get an initial exposure to these concepts in a fun context.

They really loved how the triangles curved around from small to large in Square Roots of Sixteen. Although they did not know that the color pattern had a specific meaning—the 3 dark gray triangles have hypotenuses whose lengths are whole numbers (the square roots of 4, 9, and 16); the 6 white triangles have hypotenuse lengths that are irrational and are square roots of even integers (2, 6, 8, 10, 12, 14); the 6 tan triangles have hypotenuses whose lengths are irrational and are square roots of odd integers (3, 5, 7, 11, 13, 15)—they much enjoyed describing the pattern and making up their own rules for how to extend the pattern. Sessions with this age group should be kept short, around 20 minutes, to be meaningful, and it is very helpful to end with a reading of Johnson's most famous children's book, Harold and the Purple Crayon.

Classroom Application #4: Slide Rules and Logarithmic Calculations

Keuffel & Esser Log Log Duplex slide rule, model 4092-3, ca 1936, Smithsonian Institution negative number 85-7411.

Slide rules are popular and readily available objects to bring into the classroom, where they may engage students in the visual experience of problem-solving, illustrate the connections between mathematics and real-life problems, and increase students' appreciation for history. The Wikipedia article gives enough information to get started; several websites offer more extensive primers on how to operate slide rules, including the Oughtred Society and the 1929 manual Teach Yourself the Slide Rule by Burns Snodgrass, formatted for the web by collector Ron Manley. The online version of Cliff Stoll's May 2006 article in Scientific American, “When Slide Rules Ruled,” included printable scales and instructions for making a paper linear slide rule. Vintage slide rules, some never removed from their original packaging, are constantly available on auction sites such as eBay, ranging from a few dollars for common, mass-produced models, to hundreds of dollars for rare, museum-quality examples. The easiest way to procure enough slide rules for an entire class, though, is to take advantage of the Loaner Program offered by Mike Konshak's online International Slide Rule Museum.

Classroom Application #5: Planimeters and Green's Theorem

Amsler type 2 polar planimeter, sold by Crosby Steam Gage & Valve, 1880s, Smithsonian Institution negative number 73-1252.

A planimeter is a 19th-century invention that measures the area inside a closed curve. The user sets up the device and traces the curve with a metal point. Moving the tracer arm displaces a measuring wheel according to an integral function; basically, the net roll of the wheel is proportional to the area inside the curve. After tracing the curve, the user reads the area off the measuring wheel.

The planimeter was intended to be a tool for professional practice, but it has also come to be employed in teaching mathematics. For 19th-century surveyors, machinists, and engineers, we might say that the instrument offered “integrating without integration,” a way to solve recurring problems without having to work through the underlying computations. A quick perusal of the tables of contents in journals such as Annals of Mathematics, Mathematical Gazette, and the American Mathematical Monthly suggests that, for mathematicians at the turn of the 20th century, planimeters offered an opportunity to demonstrate mathematical theory in daily life, from the operation of steam engines to data collection in the biological sciences. While mathematics professors at that time talked about teaching students to use planimeters as a means of checking their work, in its periodic rediscoveries since then, educators have brought planimeters into the classroom chiefly for illustrating Green's Theorem (the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C, it is named after George Green, and is the two-dimensional special case of the more general Stokes' theorem.). For instance, see the following references:

Eggers, John. “The Compensating Polar Planimeter.” University of California-San Diego, 2010. http://www.math.ucsd.edu/~jeggers/Resources/planimeter_slides.pdf. Walks readers through the mathematics of the instrument.

Foote, Robert L., and Ed Sandifer. “Area Without Integration: Make Your Own Planimeter.” In Hands on History: A Resource for Teaching Mathematics, edited by Amy Shell-Gellasch (Washington, DC, 2007), 71–88. Historical background on planimeters and suggestions for several classroom activities, including constructing a polar planimeter from TinkerToys®. Foote has several working papers housed on arXiv and a companion website, http://persweb.wabash.edu/facstaff/footer/Planimeter/PLANIMETER.HTM.

Leise, Tanya. “As the Planimeter's Wheel Turns: Planimeter Proofs for Calculus Class.” College Mathematics Journal 38, no. 1 (2007): 24–31. Gives formulas for a variety of forms of planimeter.

The National Museum of American History (NMAH) object group illustrates the influence of two Swiss makers and a particular story of American innovation; exploring these stories could lead to collaborations with history, business, and engineering faculty. First, in 1854 Jacob Amsler, a teacher and mathematician, made a planimeter by joining two metal arms, one with a weight that held the instrument in place, and one with a tracer point that moved along the curve. He placed a measuring wheel at the hinge, along with a vernier for increasing the precision with which measurements could be read. He based the instrument on polar coordinates. Although exact figures are not available for other forms of planimeters sold in the 1850s, Amsler's price of $20.00 was likely considerably lower than the competition. In its first 60 years, Amsler's firm made and distributed over 50,000 polar planimeters in Europe and the United States. Nine of these are in the NMAH mathematics collections.

Compensating polar planimeter, made by Gottlieb Coradi's workshop, sold by Keuffel & Esser, 1914, Smithsonian Institution negative number DOR2011-5278.

Other workshops adapted the general form of Amsler instruments, including Gottlieb Coradi, who established a workshop in Zurich in 1880 and began making wheel and disc polar planimeters in the Amsler style soon thereafter. In 1894, he modified the design into the "compensating" polar planimeter by raising the pole arm higher than the tracing arm and connecting the arms with a ball joint instead of a hinge. This allowed the user to trace in both the clockwise and counterclockwise directions, preventing errors introduced by planimeters made in the Amsler style. Of course, this instrument also cost more than Amsler planimeters: around 1910, the Coradi firm charged $36.00 for the fixed arm version and $47.00 for an instrument with an adjustable pole arm, like this one. From about 1900, the firm also made rolling sphere planimeters. One nice feature of the Coradi planimeters for museum curators is that the firm put a label inside each case with the specific calibration for the instrument and the exact date on which each planimeter was manufactured. Seven instruments from the Coradi workshop are at NMAH.

Steam engine indicator made by American Steam Gauge Co., early 20th century, Smithsonian Institution negative number RWS2011-01724.

In the United States, planimeters were frequently used to read the diagrams produced by steam engine indicators. The indicator records the pressure in a cylinder of a steam engine while the piston moves through one cycle, so that a factory foreman could monitor the conditions inside the steam engine. The pencil attached to the indicator recorded motion in two directions, the movement of the piston and the changes in pressure, which is why a drawing of a closed curve was produced. Designing indicators was big business in the late 19th and early 20th centuries, and the companies that manufactured indicators typically also sold planimeters for determining the area of steam engine indicator diagrams. Twelve planimeters in the object group were made in the United States; eight of these were manufactured specifically for reading the diagrams created by steam engine indicators. John Coffin of Syracuse, New York, patented a design in 1881 that was manufactured by the Ashcroft Manufacturing Company and, later, the John S. Bushnell Company. Both firms were located in New York City in the late 19th and early 20th centuries. Edward Jones Willis of Richmond, Virginia, also received several patents for planimeters. One of his designs was made and sold by James L. Robertson & Sons, another steam engine indicator manufacturer located in New York City.

Bushnell-Coffin linear planimeter manufactured by John S. Bushnell Company and sold by American Schaeffer & Budenberg Corporation, 1923–1937, Smithsonian Institution negative number DOR2013-001060.

Classroom Application #6: Sectors and Proportional Triangles

Mathematical instruments that are called “sectors” are usually made of two arms, or rulers, of equal length. The rulers are joined by a hinge and marked with various proportional, numerical, trigonometric, and logarithmic scales. Distances between or within scales are measured with a pair of dividers, a drawing compass with points at the end of both legs. Problems are solved by creating similar triangles based on these distances. Sectors were used from the late 16th century to the 19th century, when they were supplanted by slide rules and other instruments. The National Museum of American History (NMAH) owns examples of three main types of sectors, those made on the Italian peninsula, those made in France, and those made in England. As with any of the object groups, images can be easily downloaded to illustrate classroom presentations.

Sector in the English style, signed by Jesse Ramsden, 1765–1800, Smithsonian Institution negative number DOR2012-2586.

It takes some imagination for instructors to extend the information found in the sectors object group. Unlike some calculating and drawing instruments, it is not easy to procure historic sectors. Brass Italian and French sectors usually sell for hundreds of dollars, wooden English sectors are rare since they were often destroyed by heavy use, and recently-increased restrictions on the sale of ivory make it impossible for Americans to buy or sell ivory English sectors. Also, almost no one has written about how to make replica sectors or scales. One of the editors of Popular Woodworking Magazine has posted a video demonstrating how to convert a folding ruler into an oversized wooden sector with a “line of lines” scale (for solving proportionals and for dividing a line into any number of parts). The online Slide Rule Museum has printable scales for making slide rules, which can be adapted to teaching about sectors by editing for the logarithmic, numerical, and trigonometric scales. There are rules for calculating the scales at the bottom of the page. Some early modern works on sectors have been digitized for GoogleBooks or the Internet Archive, such as Edmund Gunter’s The Description and Use of the Sector, Crosse-Staffe, and Other Instruments, 2nd ed. (London, 1636). 19th-century English makers' catalogs and manuals on mathematical instruments often have at least a brief account of how sectors are made and used, such as John Fry Heather’s A Treatise on Mathematical Instruments, 2nd ed. (London, 1853).

Classroom Application #7: Spherometers and Basic Trigonometry

A spherometer is a device for measuring the curvature (positive or negative) of a surface, usually a convex lens made by an optometrist or lenses and mirrors used in telescopes.

Clark Spherometer, 19th century, Smithsonian Institution negative number DOR2014-05922.

The three legs of the device sit on the object to be measured, such as a lens. A micrometer (very precise screw) is lowered in the middle until it just touches the surface. The distance of the crown of the curve from the plane of the three legs is read off the micrometer on the spherometer. This measurement is the sagitta, denoted by \(h\) in the diagram below. Deriving the radius of curvature, \(R,\) from \(h\) involves a considerable amount of simple right triangle trigonometry that students can figure out on their own. For instance, the side length of the equilateral triangle formed by the three legs can be denoted by \(a\). Then some nice right triangle geometry shows that the distance from one leg to the center of the spherometer is \({\frac{a}{\sqrt{3}}}.\) From this, the formula for the radius of curvature, \(R,\) can easily be found: \[R={\frac{a^2}{6h}}+{\frac{h}{2}}.\] The figures below show \(R,\) \({\frac{a}{\sqrt{3}}},\) and \(h\), in top and side views of the surface being measured.

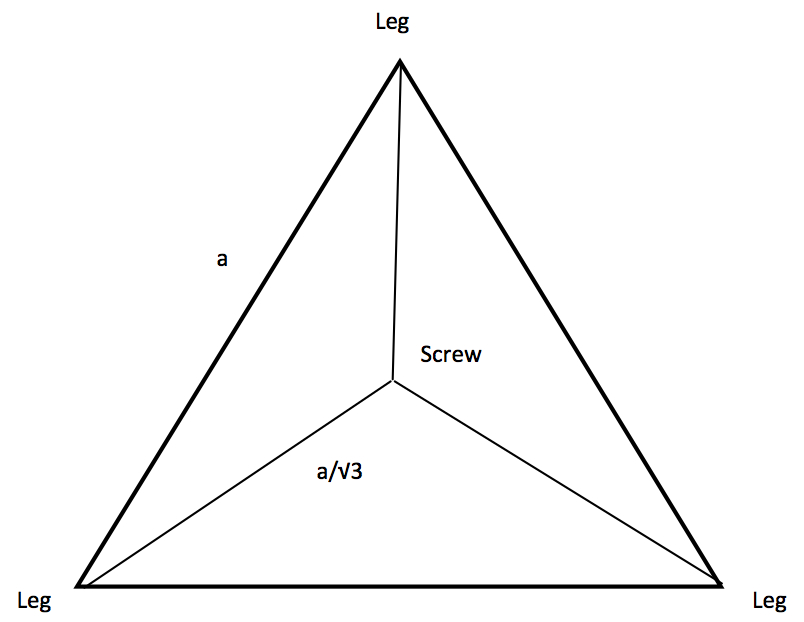
Top view diagram of the distance between the legs and central screw of a spherometer measuring a radius of curvature.

Side view diagram of a spherometer measuring the radius of curvature, R, of a curved surface.

Since spherometers are not commonly found, a simple one can be made by students or the instructor in fairly short order. Here is one Amy Shell-Gellasch made for her students to demonstrate how the device works.

Cardboard and screw spherometer constructed by Amy Shell-Gellasch.

Classroom Application #8: Kinetic Models and Calculus

The cycloid is a favorite topic in many calculus classes. The classic cycloid is the path traced by a point on the circumference of a circle as the circle rolls along a straight path. However, the cycloid is one member of a whole class of curves called trochoids: the paths generated by a point anywhere on the radius or extension of the radius of a circle as the circle rolls along another curve, usually a line or another circle.

The National Museum of American History (NMAH) houses several kinematic models published by Martin Schilling in the late 19th century that depict various kinds of trochoids. The images of these items, such as this one showing three epitrochoids, can be used in a calculus classroom. They can be shown simply as a visual aid during the discussion of trochoids and the mathematics behind them, or the images can be given to students as part of a project to explore and discuss the mathematics and uses of trochoids.

Kinematic Model of Hypotrochoids by Martin Schilling, series 24, model 3, number 331, ca 1900, Smithsonian Institution negative number DOR2013-50214.

To further illustrate the development of the various trochoids, a Spirograph® toy provides the perfect in-class demonstration. The Spirograph comes with circles, bars, discs and other fun shapes that can be rolled around or inside each other. One can produce the same curves shown in the three NMAH Schilling models that produce trochoids. The collection also includes a Schilling model that produces the involute of a circle, another popular calculus topic. The involute is easily modeled in class with a disc and piece of string.

Resources

Adler Planetarium. Webster Signature Database. http://historydb.adlerplanetarium.org/signatures/. Provides brief information on the makers of instruments owned by a variety of museums.

Booker, Peter Jeffrey. A History of Engineering Drawing. London: Chatto & Windus, 1963. Discusses the development of the subject and its teaching in the 19th and 20th centuries.

Bud, Robert, and Deborah Jean Warner, eds. Instruments of Science: An Historical Encyclopedia. New York and London: Garland Publishing, 1998.

Dawes, Howard. Instruments of the Imagination: A history of drawing instruments in Britain, 1600–1850. The Dawes Trust Ltd., 2009. Collector's discussion of historical drawing instruments, particularly those used in architecture.

Dickinson, H. W. “A Brief History of Draughtsmen's Instruments.” Transactions of the Newcomen Society 27 (1949–1951): 73–84. Overview of the major types of instruments used in surveying and engineering drawing.

Hambly, Maya. Drawing Instruments, 1580–1980. London: Sotheby's Publications, 1988. Thorough and richly illustrated treatment of a full range of instruments.

Heather, J.F. Mathematical Instruments: Their Construction, Adjustment, Testing, and Use. Rev. ed. 3 vol. London: Crosby Lockwood and Co., 1870. Describes the manufacture and use of various calculating and drawing instruments.

Kidwell, Peggy A., Amy Ackerberg-Hastings, and David L. Roberts. Tools of American Mathematics Teaching, 1800-2000. Baltimore: The Johns Hopkins University Press, 2008.

Kiely, Edmond R. Surveying Instruments: Their History and Classroom Use. National Council of Teachers of Mathematics 19th Yearbook. New York: Bureau of Publications, Teachers College, Columbia University, 1947.

Riches, David M.Mathematical Instruments: A Private Collection. http://www.mathsinstruments.me.uk/index.html. Riches is a collector who has gathered photos and information on a variety of scientific and drawing instruments.

Shell-Gellasch, Amy, ed. Hands on History: A Resource for Teaching Mathematics. Mathematical Association of America Notes No. 72. Washington, DC, 2007.

Shell-Gellasch, Amy, and Richard Jardine, eds. From Calculus to Computers: Using the Last 200 Years of Mathematical History in the Classroom. Mathematical Association of America Notes No. 68. Washington, DC, 2005.

Stanley, Philip E., ed. A Source Book for Rule Collectors. Mendham, N.J.: Astragal Press, 2003. Compilation of articles on various types of rulers, reprints of primary sources, and other historical accounts.

Stanley, William Ford. Mathematical Drawing and Measuring Instruments. 6th ed. London: E. & F. N. Spon, 1888. Classic 19th-century treatise on the manufacture and operation of various instruments.

About the Authors

Amy Ackerberg-Hastings earned a Ph.D. in the history of technology and science from Iowa State University in 2000 and teaches historical research methods and writing at the University of Maryland University College. From 2011 to 2013, she was a project assistant at the National Museum of American History, where she prepared ten of the object groups profiled in this article. She has written about the history of mathematical instruments for the MAA, the Canadian Society for History and Philosophy of Mathematics, the Johns Hopkins University Press, and the International Journal on the History of Mathematics Education.

Amy Shell-Gellasch received her Doctor of Arts degree in mathematics from the University of Illinois at Chicago in 2000, teaches mathematics at Montgomery College in Rockville, MD, and serves as a Behind-the-Scenes volunteer at the National Museum of American History. She has edited three MAA volumes on using history to teach mathematics: From Calculus to Computers: Using the Last 200 Years of Mathematics History in the Classroom, Hands on History: A Resource for Teaching Mathematics, and Mathematical Time Capsules.