A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation
Overview
Dynamic representations help make Omar Khayyam's marvelous, yet seldom-seen, approach to solving one form of a cubic equation accessible, encouraging student engagement with Khayyam's 11th-century solution in an undergraduate history of mathematics course.
A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - Introduction
Introduction
 |
| Figure 1. Statue of Omar Khayyam in Nishapur, Iran (photographed by Muhammad Mahdi Karim, December 2011, Wikimedia Commons, licensed under GFDL 1.2) |
This paper provides an example of how technology can benefit student engagement and facilitate greater appreciation for Omar Khayyam's eleventh-century approach to constructing a solution to a cubic equation. The GeoGebra applet included here presents the result of Khayyam's marvelous construction in a format more accessible to modern readers than his writings in translation. This dynamic representation eliminates the difficulty of visualizing and interpreting a static image from Khayyam's proof, thus surmounting some of the obstacles to and maintaining the benefits of including Khayyam's solution in an undergraduate course in the history of mathematics.
Studying primary sources from the history of mathematics is one way to foster an understanding of mathematics as an ongoing, creative process that occurs in specific times and places. Primary sources can also illuminate gradual change, including incremental shifts in perspective that do not persist as part of our current mathematical landscape. Although primary source material provides these rich opportunities for mathematical and historical insights, students often find it frustrating to deal with archaic sources that originate in a profoundly different worldview. Linguistic and notational differences pose challenges, too. Students are sometimes uninterested in overcoming these difficulties, especially when they know simpler, more efficient, or more general modern methods – as in the case of solutions for polynomial equations of small degree. This paper presents an accessible, interactive format designed to remove difficult realities of studying a primary source while retaining Khayyam's remarkable mathematical result.
A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - Polynomials in History of Mathematics Courses
Since algebra is a foundational component of modern mathematics very familiar to undergraduates, it can provide a helpful touchstone throughout a history of mathematics course. Investigating the treatment of finding solutions for polynomial equations can provide a nice coherence to a range of material from ancient Greece through Niels Henrik Abel's nineteenth-century proof that no general solution exists for a quintic equation. Along the way, students encounter the work of Diophantus, al-Khwarizmi, Cardano, Viete, Descartes, Recorde, Newton, Euler, Lagrange, Gauss, Ruffini and many others as a notion emerges of algebra as a generalized problem-solving tool. This focus encourages students to think about how mathematical practitioners throughout history have dealt with similar kinds of problems. These investigations also can be used to highlight particular features of the historical context, perhaps a view of the purpose of mathematics, or the role of abstraction, or the nature of mathematical justification. The investigation of equation-solving also raises significant questions about the nature of notation and the development of algebra.
While the modern framework of algebraic solutions to polynomial equations can aid student understanding, it can also hinder deeper appreciation for the nuance of historical mathematics in context. So familiar is the modern notion of a quadratic equation of the form \(ax^2 + bx + c = 0\) solvable by the quadratic formula, that it is easy to read modern ideas into an historical text. It is indeed a challenging mental exercise to think in a context that allows only positive integer coefficients – a place where \(x^2+ bx = c\) fundamentally differs from \(x^2 + c = bx\) – or to imagine a mathematical world where \(x^2\) literally represents a square and dimensionality fundamentally matters in a polynomial-like expression. The way historical practitioners approached these problems can feel very unnatural to modern students.
The demonstration here is designed to minimize these difficulties so students can first understand the result of Khayyam's construction before delving into historiographical questions. In particular, the GeoGebra applets connect Khayyam's geometrical approach to the cubic and a familiar cubic graph so that students can visualize the relationship between Khayyam's construction and the idea of \(x\)-intercepts as roots of the polynomial. The modern software furthermore allows a dynamic representation that enables students to explore this relationship for a variety of cubic equations. The modern technology provides scaffolding for students to understand Khayyam's construction and result. This knowledge will then support further historical discussion about what Khayyam's static image communicates about his own mathematical context.
A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - A Common Cubic Narrative
In a general History of Mathematics survey course, the work of Girolamo Cardano is a common focal point for studying a general solution to the cubic. Cardano's well-known solution to the cubic appeared in Ars Magna in 1545 and is often credited as the first publication of a general solution to cubic equations.

Figure 2. The title page of Cardano's Ars Magna in Convergence's Mathematical Treasures (image courtesy of Columbia University Libraries).
Students usually encounter Cardano's solution either with 3D manipulatives of the type described by William Branson (Branson), or in terms of an algebraic formulation as done by William Dunham (Dunham, pp. 133-146). Not only does Cardano's method offer a very satisfying intersection of algebraic and geometric methods, but the related historical narrative is rich with drama and intrigue, briefly outlined below (Fauvel and Gray, pp. 253-254).
Scipione del Ferro, a fifteenth-century mathematics professor at the University of Bologna, knew a method of algebraic solution for equations of the form “cube and things equal to numbers,” or \(x^3 + ax = b\) with \(a, b > 0\). At some point, del Ferro shared his guarded knowledge with his student Antonio Maria Fióre, who proceeded to make a living by challenging others to mathematical problem-solving contests. Since Fióre knew del Ferro's secret, he always posed problems of the form \(x^3 + ax = b\). Fióre's trick worked until he challenged Niccoló Tartaglia in 1535.

Figure 3. Niccoló Tartaglia (1499-1557), from Convergence's Portrait Gallery. (This image was provided by the Dibner Library of Science and Technology, The Smithsonian Institution Libraries, and its use must conform to the Library’s rules and standards.)
Tartaglia developed his own solution and won the contest (although he declined Fióre's prize of 30 free dinners). Word of Tartaglia's fame and accomplishment reached Girolamo Cardano in Milan. After a long campaign, Cardano convinced Tartaglia to meet with him in 1539 to divulge the secret in verse on the condition that Cardano swear not to publish it. Cardano and his student Ludovico Ferrari subsequently learned that del Ferro knew the solution method. Since they also developed the material further, discovering how to solve other types of cubics, and, thanks to Ferrari, also quartics, they decided to publish this work in Ars Magna in 1545. The enraged Tartaglia fought bitterly against Cardano and Ferrari for years afterwards.

Figure 4. Girolamo Cardano (1501-1576), from Convergence's Portrait Gallery.
The hint Cardano initially got from Tartaglia worked only for a special class of cubics of the form \(x^3 + ax = b\) with \(a, b > 0\). For contemporary readers, of course, \(ax^3 + bx^2 + cx + d = 0\) encompasses all possible cases, where the coefficients are positive, or negative, real, or imaginary. Prior to the widespread adoption of negative numbers, though, mathematical practitioners considered each possible combination of positive coefficients for a cubic equation. It is, naturally, difficult (if not impossible) for students to imagine practicing mathematics without the generalized problem-solving tools of modern algebra. It is likewise often challenging for students to appreciate how, in context, Tartaglia had actually given Cardano the solution to one type of cubic. Cardano then continued working with Ferrari to extend the result to include other types of cubics. In total, they investigated fourteen types of cubic equations. Due to these efforts, Cardano's name is now attached to the three equations that give the three roots of the modern cubic equation \(ax^3 + bx^2 + cx + d = 0\), which encompasses all the various forms of medieval cubics.
Although Cardano gets significant credit, he and his fellow Italian mathematicians were certainly not the first to grapple with solutions of cubic equations. Some ancient Babylonian tablets from the 20th-16th centuries BCE have tables for calculating cubes and cube roots, although there is no evidence they used these tables to solve equations. The doubling of a cube is a well-known problem of classical antiquity attempted by mathematical practitioners including Hippocrates, Menaechmus, and Archimedes, although it is extremely unlikely that any of them formulated the problem in terms of a cubic equation (Aminrazavi and Van Brummelen). The Nine Chapters on the Mathematical Art, a classic Chinese text compiled around the 2nd century BCE, includes some methods for solving some cubic equations. In 7th century China, Wang Xiaotong solved 25 cubic equations of the form \(x^3+px^2+qx=N\) (Mikami, pp. 53-56). In the 11th century, Omar Khayyam contributed a geometric solution to the theory of cubic equations. In twelfth-century India, Bhaskara II attempted the solution of cubic equations. In Persia, Sharaf al-Din al-Tusi treated several types of cubic equations in his Treatise on Equations. The treatment of cubics additionally occupied many other mathematical practitioners from the 9th through the 16th centuries (Aminrazavi and Van Brummelen).
These considerable efforts are often overlooked in undergraduate history of mathematics survey classes. There are many defensible explanations for this, ranging from lack of space in a semester syllabus to the challenges – linguistic, cultural, and mathematical – posed by the material itself. The GeoGebra applet included here aims to highlight one of these seldom-seen investigations in an accessible way. Omar Khayyam's constructive solution to the cubic serves as one example from the richly textured history of work on finding solutions to cubic equations. The use of GeoGebra software removes the difficulty of interpreting Khayyam's static diagram, enabling students to focus on appreciating the construction and understanding the justification that the constructed segment is, in fact, a solution. This dynamic visualization also links Khayyam's construction with a modern Cartesian graph of a cubic equation. Students can interact with this dynamic representation, making Khayyam's remarkable work more accessible and engaging, and thus easier to integrate into a History of Mathematics course.
A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - Omar Khayyam and Cubic Equations
Khayyam's full name, Abū’l-Fath Ghiyāth al-Dīn ‘Umar ibn Ibrāhīm al-Khayyāmī al-Nīshāpūrī, suggests that his family trade was making tents, but his modern reputation hinges on the poetry, mathematics, and philosophy he generated in a region near present-day Afghanistan. Biographical information on Khayyam is taken from the article about him in the Dictionary of Scientific Biography (Rosenfeld and Youschkevitch).
Khayyam may be most well-known for his Rubā’iyāt quatrains which critique the fundamental tenets of religion through discussion of issues such as epistemology, eschatology, determinism, and quest for meaning. In mathematics, Khayyam worked within an Islamic tradition of investigating Euclid's parallel postulate and discussing the definition of ratios. In addition to producing a thorough investigation of cubics, Khayyam also discovered a general method for root extraction of arbitrarily high degree. He appears to have arrived at questions about cubic equations through his investigation of geometrical problems.
In a translated excerpt of Khayyam's work, he discussed a “square square,” or, for modern readers, an \(x^4\) term, as something that “does not exist in reality in any way,” but instead in the realm of philosophy (Fauvel and Gray, p. 226). He continued to say “whatever is obtained by algebra is obtained” by four things: “number, object (\(x\)), square (\(x^2\)), and cube (\(x^3\)).” Dimensionality provided the justification for this. Khayyam specified that number is “a state of mind independent of all magnitudes. This does not exist in reality.” Khayyam clarified that “number only comes into existence when it is denoted by a material cause.” For Khayyam, a straight line denoted the object familiar to modern readers as \(x\). A square, which we denote by \(x^2\), Khayyam “denoted by a quadrilateral of equal sides with right angles whose side is equal to a straight line.” And, finally, he described a cube, known to us as \(x^3\), as “a solid which is bounded by six equal surfaces of four sides whose sides are equal, angles are right angles.” Those four sides were each straight line objects, or, for us, \(x,\) and each surface was a square; in our notation, \(x^2\). Khayyam referenced Euclid's Elements (XI, 27) for the construction of a cube and asserted that “an object with more than three dimensions is impossible” (Fauvel and Gray, p. 226).
Khayyam stated that methods for finding unknowns for the six different forms of quadratic equations have been thoroughly “explained in books of algebraists” (Fauvel and Gray, p. 226). In fact, ruler and compass constructions to solve quadratic equations and similar methods date as far back as the Greeks. Khayyam would have been familiar with both the Elements of Euclid and the Conics of Apollonius. Khayyam enumerated the following types of cubic polynomials listed as equations (0.1) to (0.19) below. He used the language of “a cube equal to squares” for what the modern reader will recognize as \(x^3 = ax^2\), or “a cube plus edges equal to squares and numbers” for \(x^3 + ax = bx^2 + c,\) and so on, but we adopt polynomial notation here.
| (0.1) | \(x^3\) | \(= ax^2\) | ||
| (0.2) | \(x^3\) | \(= ax\) | ||
| (0.3) | \(x^3\) | \(= a\) | ||
| (0.4) | \(x^3 + ax^2\) | \(= b\) | ||
| (0.5) | \(x^3 + ax^2\) | \(= bx\) | ||
| (0.6) | \(x^3 + a\) | \(= bx\) | ||
| (0.7) | \(x^3 + a\) | \(= bx^2\) | ||
| (0.8) | \(x^3 + ax\) | \(= b\) | ||
| (0.9) | \(x^3 + ax\) | \(= bx^2\) | ||
| (0.10) | \(ax^2 + bx\) | \(= x^3\) | ||
| (0.11) | \(ax^2 + b\) | \(= x^3\) | ||
| (0.12) | \(ax + b\) | \(= x^3\) | ||
| (0.13) | \(x^3\) | \(= ax^2 + bx + c\) | ||
| (0.14) | \(x^3 + ax\) | \(= b + cx^2\) | ||
| (0.15) | \(x^3 + ax^2 + b\) | \(= cx\) | ||
| (0.16) | \(x^3 + ax^2 + bx\) | \(= c\) | ||
| (0.17) | \(x^3 + ax^2\) | \(= bx +c\) | ||
| (0.18) | \(x^3 + ax\) | \(= bx^2+c\) | ||
| (0.19) | \(x^3 + a\) | \(= bx^2 + cx\) |
Because the coefficients \(a\), \(b\), and \(c\) must be greater than zero for Khayyam, these represented different forms of cubic equations. Equations (0.1), (0.2), (0.5), (0.9), and (0.10) are solvable by methods from Euclid's Elements, Book II. Finding solutions for the remaining fourteen cubic equations required solid geometry, specifically conics and conic sections.
To contemporary students, a geometric solution to a cubic equation may seem strange. Exploring this approach poses a challenge of communicating how geometric problems motivated the study of cubic equations. Medieval Islamic algebra is, in many ways, a foreign terrain both conceptually and notationally. We do not have access to sources that reveal the particular insight that led to Khayyam's construction. In fact, this is a common situation when dealing with historical mathematics. Rarely do we have access to the developmental process of historical practitioners of mathematics. One exceptional example is the recent discovery of a previously unknown text, The Method, by Archimedes, that resolved centuries of questions about how he generated the formulas he proved by methods of contradiction. For now, we have no such insight in the case of Khayyam. This foray into medieval Islamic mathematics nonetheless invites discussion of the mathematical environment and tools available to Khayyam – as well as how they differed from those of Cardano and others. Encountering the perspective that powers of \(x\) correspond to actual geometrical dimensions is also a valuable addition to a student's experience of historical mathematics. In this context, bounded in ways by three dimensions of physical space, the solution of a cubic equation marked a significant achievement.
A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - Khayyam's Construction
Khayyam began by providing directions from which the reader can construct a line segment that is the solution to a polynomial of the form “cubes and squares and roots equal a number” (Fauvel and Gray, p. 233). Note that “cubes” corresponds to a modern \(x^3\) term. Likewise, Khayyam's “squares” would be \(x^2\) and his “roots” \(x.\) Modern notation expresses this sum of cubes, squares, and roots equal to a number in the form \(x^3 + C_1x^2 + C_2x = C_3,\) with \(C_1, C_2, C_3>0.\) In Khayyam's proof (Fauvel and Gray, pp. 233-234), he treated each of these terms as a parallelepiped volume, suggesting a contemporary articulation of the form \(x^3 + ax^2 + b^2x = c^3.\) (For example, in the cubic \(x^3 + 4x^2 + 6x = 8,\) values for the construction would be \(a = 4,\) \(b = {\sqrt{6}},\) and \(c = 2.\)) The following set of instructions constructs a line segment \({\overline{x}},\) whose length \(x\) is a solution to a cubic equation of the form \(x^3 + ax^2 + b^2x = c^3,\) \(a, b, c >0.\) The result of this construction can be seen in Figure 5, and Figure 6 is a movie showing all steps of this construction.

Figure 5. Khayyam's construction, in which line segment \(\overline{LB}\) (for Khayyam) or its length \(LB\) (for us) is a solution to the cubic equation \(x^3 + ax^2 + b^2x = c^3,\) where \(a, b, c >0.\)
First, Khayyam said to construct a line segment \(\overline{HB}\) of length \(b\), the square root of the given number of edges. Then build a rectangular solid of volume \(c^3\) whose base is a square with sides of length \(b\). Construct a line segment \(\overline{BG}\) perpendicular to \(\overline{HB}\) so that the length of \(\overline{BG}\) is the height of this rectangular solid. Since the area of the base is \(b^2\) and the volume \(c^3\), then in terms of coefficients of the modern polynomial, \(\overline{BG}\) is of length \(\frac{c^3}{b^2}.\) The final piece of the construction utilizing given information is to put point \(D\) in line with line segment \(\overline{GB}\) such that \(\overline{DB}\) is a line segment of length \(a.\)
Next, construct a semi-circle with diameter \(\overline{GD}\). In Khayyam's diagram, this is the semi-circle in the upper half plane. The line segments \(\overline{GB}\) and \(\overline{HB}\) then determine a rectangle that is completed by adding point \(K\) and line segments \(\overline{GK}\) and \(\overline{HK}\). Draw then a hyperbola passing through point \(G\) with asymptotes \(\overline{HK}\) and \(\overline{HB}\). This hyperbola will intersect the semicircle again at a known point \(Z\). Drop a line from \(Z\) perpendicular to diameter \(\overline{GD}\) that intersects \(\overline{GD}\) at point \(L\) and intersects line segment \(\overline{KH}\) at point \(T\). Khayyam asserted that the line segment \(\overline{LB}\) is the solution to the cubic, whereas we would say that its length \(LB\) is a solution. The conflation of a line segment and its length may appear sloppy to modern readers, but this is faithful to Khayyam's presentation, in which the line segment is viewed as the solution.
At this point, although Khayyam had constructed the segment which satisfies the given cubic, his instructions continued in order to complete the geometrical constructions necessary to justify \(\overline{LB}\) as a solution. So, he said, draw a line through point \(Z\) perpendicular to the line segment \(\overline{ZLT}\) just constructed. Extend line segment \(\overline{HB}\) to intersect that line at point \(A\). These rectangles concluded Khayyam's construction.
Khayyam's construction is illustrated dynamically in the two-minute movie and the interactive applet in Figures 6a and 6b below.
Figure 6a. Khayyam's construction, in which the length \(LB\) of the line segment \(\overline{LB}\) is the positive solution to the cubic equation \(x^3+7.9x^2 +{{1.3}^2}x={2.1}^3.\) This solution is shown as a zero on the graph of the cubic function \(f(x) = x^3+7.9x^2 +{{1.3}^2}x-{2.1}^3\) at right. After starting the two-minute movie, to make the viewing window larger, click the "Full screen" icon in the lower right corner. To return to this article, press the Escape key.
Figure 6b. Khayyam's construction, in which the length \(LB\) of the line segment \(\overline{LB}\) is the positive solution to the cubic equation \(x^3+7.9x^2 +{{1.3}^2}x={2.1}^3.\) This solution is shown as a zero on the graph of the cubic function \(f(x) = x^3+7.9x^2 +{{1.3}^2}x-{2.1}^3\) at right. Use the arrows to click through each step of the construction, or click the circular "Play" (or "Pause") icon to see the slideshow. The box labeled "s" may be used to change the speed of the slideshow. Finally, to change the cubic equation, adjust the sliders for coefficients \(a,\) \(b,\) and \(c.\)
Intermingled with the above instructions is a justification that the constructed line segment \(\overline{LB}\) indeed satisfies the cubic. A presentation of Khayyam's argument follows on the next page. Key steps are highlighted and explanations of geometric facts perhaps less familiar to modern readers are included. The main tools in Khayyam's argument are ratios and geometric reasoning, along with the properties of the hyperbola and circle.
A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - Khayyam's Geometric Demonstration
The construction gives instructions from which the reader can construct a segment that gives the solution to a polynomial of the form “cubes and squares and roots equal a number.” Because mathematical practice of the time insisted on maintaining dimensionality, it would only be possible to add terms with like dimension, so each term in the polynomial would essentially be viewed as a three-dimensional rectangular box. For Khayyam, then, finding the solution of a cubic was a geometrical question of finding the right sized line segment \(\overline{LB}\) with which three boxes can be built so that their combined volumes equal a given volume. The first box is a perfect cube with volume \((LB)^3\). The second box has a square base of area \((LB)^2\) and given height \(DB\). The third box has height \(LB\) and given square base of area \((HB)^2\). The total volume of these three boxes must be equal to the given volume \((HB)^2 \times BG\). This condition generates the cubic equation \[(LB)^3 + DB \times (LB)^2 + (HB)^2 \times LB = (HB)^2 \times BG\] in \(LB\) and Khayyam's construction yields a line segment \({\overline{LB}}\) whose length satisfies it.
Khayyam includes with the construction geometric reasoning to verify this claim. Below is a version of the proof that follows closely a translation of his presentation (Fauvel and Gray, pp. 233-234). This version outlines five key steps in the argument, with each step fully explained in turn. Below this geometric demonstration is then a suggestion for the reader to rework the argument in terms of contemporary algebraic notation, perhaps better to understand the relationship between the line segment \(\overline{LB}\) and the polynomial \(x^3 + ax^2 + b^2x = c^3\).
Step 1. First show that the areas of the rectangles \(\square GLTK\) and \(\square ZABL\) are equal.
Note that \(\blacksquare ABCD\) indicates the area of the rectangle with vertices \(A,\) \(B,\) \(C,\) and \(D,\) and \(\square ABCD\) denotes the rectangle itself.

Figure 7. Since \(\blacksquare ZAHT = \blacksquare GBHK\) and rectangles \(\square ZAHT\) and \(\square GBHK\) share \(\square LBHT\), then the areas of the green and purple rectangles are equal. The above figure shows the area computation in the case of \(x^3 + 7.9x^2 + 1.3^2 x = 2.1^3\).
Apollonius established a property of hyperbolas stating that the product of the distances from any point on the curve to each of the asymptotes is a constant. Since points \(G\) and \(Z\) are both on the same hyperbola with asymptotes \(\overline{HK}\) and \(\overline{HB}\), this means that the rectangles \(\square ZAHT\) and \(\square GBHK\) have the same area. Since these rectangles share the common rectangle \(\square LBHT\), this means the difference rectangles \(\square GLTK\) and \(\square ZABL\) also have equal area as illustrated in Figure 7.
Step 2. Next, develop the ratio \(\displaystyle\frac{(LZ)^2}{(GL)^2} = \frac{(HB)^2}{(LB)^2}.\)

Figure 8. A computed example of equal ratios \(\displaystyle\frac{(LZ)^2}{(GL)^2}\) and \(\displaystyle\frac{(HB)^2}{(LB)^2}\) in the case of \(x^3 + 7.9x^2 + 1.3^2 x = 2.1^3\).
Since we have equal areas \(\blacksquare GLTK =\) \(\blacksquare ZABL,\) this means that \((LZ) \times (LB) = (GL) \times (LT)\), so \(\displaystyle \frac{LZ}{GL} = \frac{LT}{LB}.\) Since \(HB\) is equal to \(LT\), then \(\displaystyle \frac{LZ}{GL} = \frac{HB}{LB}.\) Likewise, then, their squares will also be in proportion, which gives the ratio for Step 2.
Step 3. Then, use the semi-circle to obtain \(\displaystyle \frac{(LZ)^2}{(GL)^2} = \frac{LD}{GL}.\)
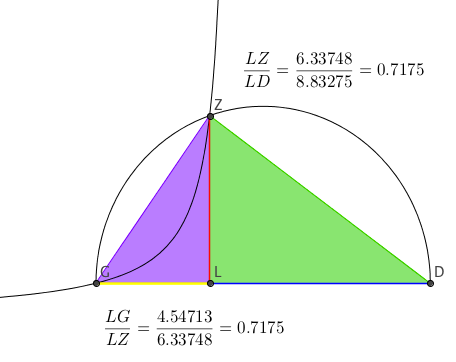
Figure 9. The green and purple triangles are similar. This yields the ratio \(\displaystyle \frac{LG}{LZ} = \frac{LZ}{LD}\), which is necessary for Step 3.
Because triangle \(\triangle DGZ\) is inscribed on the diameter in a semi-circle (as shown in Figure 9), it is a right triangle by Thales' Theorem. Then triangles \(\triangle LGZ\) and \(\triangle LDZ\) are also right triangles and, in fact, these three triangles are similar. Thus, we have \(\displaystyle \frac{LG}{LZ} = \frac{LZ}{LD}\) which gives the necessary piece for our substitution: \(\displaystyle (LZ)^2 = GL \times LD\). The equality for Step 3 follows directly.
Step 4. Next, demonstrate that \((HB)^2 \times GL = LD \times (LB)^2.\)
Combine Steps 2 and 3 above for \(\displaystyle \frac{(LZ)^2}{(GL)^2} = \frac{(HB)^2}{(LB)^2} = \frac{LD}{GL}.\) This means \((HB)^2\times GL = LD \times (LB)^2.\) Khayyam interpreted this as a geometric fact in terms of geometric solids, saying that the solid whose base is a square with sides of length of \(HB\) and height \(GL\) will have volume equal to a solid whose base is a square with sides of length \(LB\) and height \(LD\).
Step 5. Finally, verify that the length of the constructed segment \(\overline{LB}\) satisfies the cubic.
Since point \(B\) is between \(D\) and \(L\), then \(LB\) + \(DB\) = \(LD\). This means we can divide the box with base of area \((LB)^2\) and height \(LD\) into two smaller boxes: the cube with volume \((LB)^3\) plus a box with base of area \((LB)^2\) and height \(DB\). This, combined with Step 4 above, gives \[(HB)^2 \times GL = LD \times (LB)^2 = (LB + DB) \times (LB)^2 = (LB)^3 + DB \times (LB)^2.\] Now add to each side the volume \((HB)^2 \times LB\) to get \[ (HB)^2 \times GL + (HB)^2 \times LB = (LB)^3 + DB \times (LB)^2 + (HB)^2 \times LB.\] Since \(GL + LB = GB\), then \[ (HB)^2 \times GB = (LB)^3 + DB \times (LB)^2 + (HB)^2 \times LB,\] and \(LB,\) the length of the constructed line segment \({\overline{LB}},\) solves the cubic.
A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - An Algebraic Rendering of the Demonstration
A geometric solution to a cubic equation may seem peculiar to modern eyes, but the study of cubic equations (and indeed much of medieval algebra) was motivated by geometric problems. Khayyam stated in his text that the arithmetic problem of the cubic remained to be solved. In particular, he sought to articulate an algorithm for finding root(s) of a cubic equation by operating on its coefficients. He never produced such a solution; nor did anyone else until Girolamo Cardano in the mid-16th century. Readers of this article may be particularly interested to see the relationships between a modern polynomial and Khayyam's geometric treatment of a cubic.
Consider the polynomial \(x^3 + ax^2 + b^2x = c^3.\) To follow Khayyam's demonstration, take \(HB = b,\) \(DB = a,\) and \(BG = \frac{c^3}{b^2} = p.\) Recall the hyperbolic property from Apollonius that states the product of the distances from any point on the curve to each of the asymptotes is a constant. We repeat Figure 5, which illustrates Khayyam's construction, for convenience:

Figure 5. Khayyam's construction, in which line segment \(\overline{LB}\) (for Khayyam) or its length \(LB\) (for us) is the solution to the cubic.
If we take G = \((p,b)\) to be a fixed point on the hyperbola and Z = \((x,y)\) to be any point on the hyperbola, then this property for any point Z = \((x,y)\) could be written as \(pb = x(y + b)\). This would be in relation to an origin \((0,0)\) at the intersection of segments \(\overline{BH}\) and \(\overline{TH}\). Readers may wish to work through the remainder of Khayyam's justification from this modern perspective.
A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - Combining Khayyam's Construction with a Modern Graph
Notably, Khayyam's construction generates a single line segment \(\overline{LB}\) which solves the cubic equation of the form \(x^3 + C_1x^2 + C_2x = C_3,\) where \(C_1,C_2,C_3>0.\) In Figure 6 and Figure 7, for an example, we have fixed the coefficients to be \(x^3 + 7.9x^2 + 1.3^2 x = 2.1^3,\) and in Figure 10, below, our example is \(x^3 + 4.8x^2 + 1.4^2 x = 1.7^3.\) In Figure 10, we have reflected Khayyam's construction about the line \(\overline{HB},\) the vertical asymptote of the hyperbola. Then, superimposing a Cartesian graph of a cubic shows clearly that \(BL\) corresponds exactly to the positive root of the cubic.
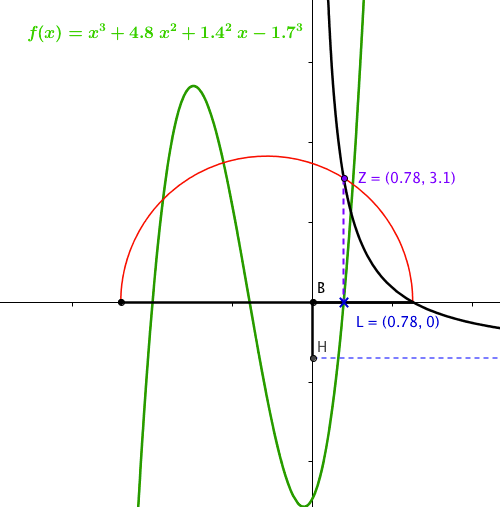
Figure 10. A reflection of Khayyam's construction for \(x^3 + 4.8x^2 + 1.4^2 x = 1.7^3,\) superimposed with a Cartesian graph of the equivalent cubic function. We take line segment \(\overline{HB},\) an asymptote for the hyperbola, as a vertical axis and line segment \(\overline{BL}\) to have length \(x\), which is exactly the value of a root to the cubic polynomial.
The slider bars in the GeoGebra applet in Figure 11 (below) enable students to explore how Khayyam's construction works for cubics with a range of coefficients. This dynamic exploration facilitates an appreciation of the general nature of the proof – Khayyam's method is not simply constructing one root to one specific polynomial. His construction technique constructs one root for any polynomial of the form \(f(x) = x^3 + C_1x^2 + C_2x - C_3,\) where \(C_1, C_2, C_3 > 0.\) The applet also presents in an accessible visual form the relationship between Khayyam's line segment \(\overline{LB}\) and a root of the cubic graph familiar to many students.
Figure 11. A reflection of Khayyam's construction for \(x^3 + ax^2 + b^2 x = c^3,\) with various positive values of \(a,b,\) and \(c,\) superimposed with a Cartesian graph of the equivalent cubic function. We take line segment \(\overline{HB},\) an asymptote for the hyperbola, as a vertical axis and line segment \(\overline{BL}\) to have length \(x\), which is exactly the value of a root to the cubic polynomial.
In Figures 10 and 11, superimposing a Cartesian graph of a cubic shows clearly that \(BL\) corresponds exactly to the positive root of the cubic. But what of the other roots?
A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - Shouldn't a Cubic Have Three Roots?
The Medieval Islamic geometrical perspective ruled out negative coefficients and solutions, but this constructive technique from Khayyam is nonetheless capable of finding all real solutions to a cubic of the form \(x^3 + C_1x^2 + C_2x = C_3.\) A few additions to the construction generate the other two real roots (if they exist). First, we need to construct the complete circle on diameter \(\overline{GD}\) and not simply the top semi-circle. Second, we need the other half of the hyperbola through point \(G\) with asymptotes \(\overline{HK}\) and \(\overline{HB}\). The lower half of the hyperbola intersects the circle at two points, or at one point of tangency, or not at all. If the lower half of the hyperbola intersects the circle at two distinct points, the \(x\)-values corresponding to those intersection points are two negative roots to the cubic. If the lower half of the hyperbola intersects the circle at a point of tangency, the \(x\)-value of that point corresponds to a repeated negative root. If the lower half of the hyperbola does not intersect the circle, then there is a pair of complex roots. We know, by Descartes' Rule of Signs, that polynomials of the form \(x^3 + ax^2 + b^2 x = c^3,\) with \(a, b, c>0,\) cannot have more than one positive root. Khayyam's construction as presented finds a single, positive root and, if enhanced by completing the circle and hyperbola, gives additional information about all roots to a cubic of the specified form.
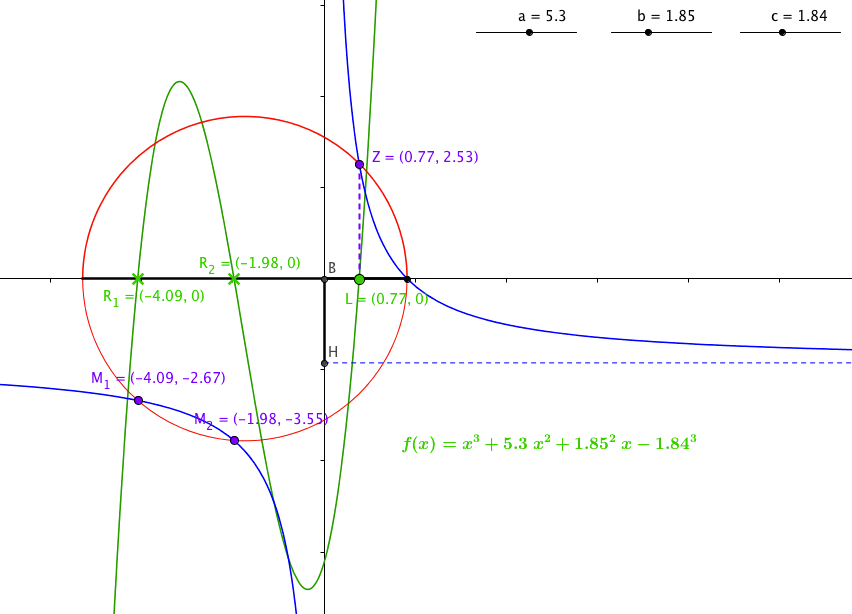
Figure 12. A reflection of Khayyam's construction for the cubic \(x^3 + 5.3x^2 + 1.85^2x = 1.84^3,\) enhanced with the complete hyperbola and both halves of the circle. The Cartesian graph of the cubic function \(f(x) = x^3 + 5.3x^2 + 1.85^2x - 1.84^3\) is superimposed on the construction. This illustrates that the \(x\)-coordinates of the points of intersection (not along the \(x\)-axis) between the circle and the hyperbola are, in fact, roots to the cubic.
Figure 13. A reflection of Khayyam's construction for the cubic \(x^3 + ax^2 + b^2x = c^3,\) enhanced with the complete hyperbola and both halves of the circle. The Cartesian graph of the cubic function \(f(x) = x^3 + ax^2 + b^2x - c^3\) is superimposed on the construction. This illustrates that the \(x\)-coordinates of the points of intersection (not along the \(x\)-axis) between the circle and the hyperbola are, in fact, roots to the cubic.
A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - Conclusion
In his Treatise on Algebra, Khayyam set out to deal systematically with solving fourteen types of cubic equations using constructions and justification based on intersecting conic sections (Rashid and Vahabzadeh). The demonstration in this article illustrates his approach in one case of the cubic, the one we wrote as equation (0.16), \(x^3 + ax^2 + bx = c,\) with \(a, b, c > 0,\) in our list in the section, Omar Khayyam and Cubic Equations. Demonstrations of Khayyam’s solution methods for the cubic in equation (0.8), \(x^3 + ax = b,\) where \(a, b > 0,\) are available at GeoGebra via the following links:
- Maurice O'Reilly, Omar Khayyam's approach to solving certain cubic equations, https://www.geogebra.org/m/nbwq58f8
- John Golden, A Cubic Solution of Omar Khayyam, https://www.geogebra.org/m/hF8Hjuv6
- Paul Rakow, Omar Khayyam's geometric solution of a cubic equation, https://www.geogebra.org/material/show/id/rTV3y4Bb
- ank3721, Khayyam_NCTM, https://www.geogebra.org/m/YZvw7sux
Like the applets in this article, these all provide examples of how technology can facilitate student engagement with substantial questions about the history of mathematics.
The use of GeoGebra software reduces the difficulty of interpreting Khayyam's static diagram, and of dissecting the dependencies inherent in the construction to see how the technique can apply to every cubic of this form. Reflecting Khayyam's construction and superimposing a Cartesian graph of the cubic also provides a useful connection between his unfamiliar approach to solving a cubic and the more familiar process of locating a root on a graph. Tools like these GeoGebra applets frame historical results in a language accessible to students so they can first understand the result – but this is not the end of the story. The twenty-first century software provides scaffolding for deeper exploration of historiographical questions.
In a mathematical context where powers of \(x\) literally corresponded to geometrical dimensions, solving cubic equations represented the height of mathematical achievement. But what did Khayyam achieve? Given the above observation, is it accurate to say that Khayyam did in fact, solve the complete cubic problem? Or did Cardano do something unimagined by Khayyam? In what ways are or are not these techniques addressing similar questions? Questions like these invite students to delve into issues of mathematical and historical context. What does it mean to attain a mathematical result? Investigating solutions to cubic equations that do not persist as the first general solution gives rise to explorations of innovation and novelty. These GeoGebra representations may provide students with an understanding of Khayyam's marvelous construction that is adequate to engage these and other questions, facilitating fruitful discussion in an history of mathematics classroom.
A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - References
References
Aminrazavi, M. and Van Brummelen, G. “Umar Khayyam,” The Stanford Encyclopedia of Philosophy (Fall 2011 Edition), Edward N. Zalta (ed.), http://plato.stanford.edu/archives/fall2011/entries/umar-khayyam
Branson, W. B. “Solving the Cubic with Cardano,” Convergence (September 2013)
http://www.maa.org/press/periodicals/convergence/solving-the-cubic-with-cardano
Dunham, W. Journey through Genius: The Great Theorems of Mathematics, Penguin Books, 1991.
Fauvel, J. and Gray, J. The History of Mathematics: A Reader, The Open University, 1987.
Mikami, Y. The Development of Mathematics in China and Japan (2nd ed.), New York: Chelsea Publishing Co., 1974.
Rashid, R. and Vahabzadeh, B. Omar Khayyam, the Mathematician, New York: Bibliotheca Persica Press, 2000.
Rosenfeld, B.A. and Youschkevitch, A. P. “Al-Khayyam,” Dictionary of Scientific Biography, 2008, Encyclopedia.com. (October 12, 2014), http://www.encyclopedia.com/doc/1G2-2830902291.html
Swetz, F.J. and Katz, V.J. “Mathematical Treasures - Ars Magna Title Page,” Convergence (May 2008), http://www.maa.org/press/periodicals/convergence/mathematical-treasures-ars-magna-title-page