Pythagorean Cuts – Extensions to Regular Polygons
Extensions to Regular Polygons
Can the notion of Pythagorean cuts be extended to, say, regular n-gons? Consider, for example, the regular hexagons built on the sides of right triangle ABC, as shown in Figure 10, below.
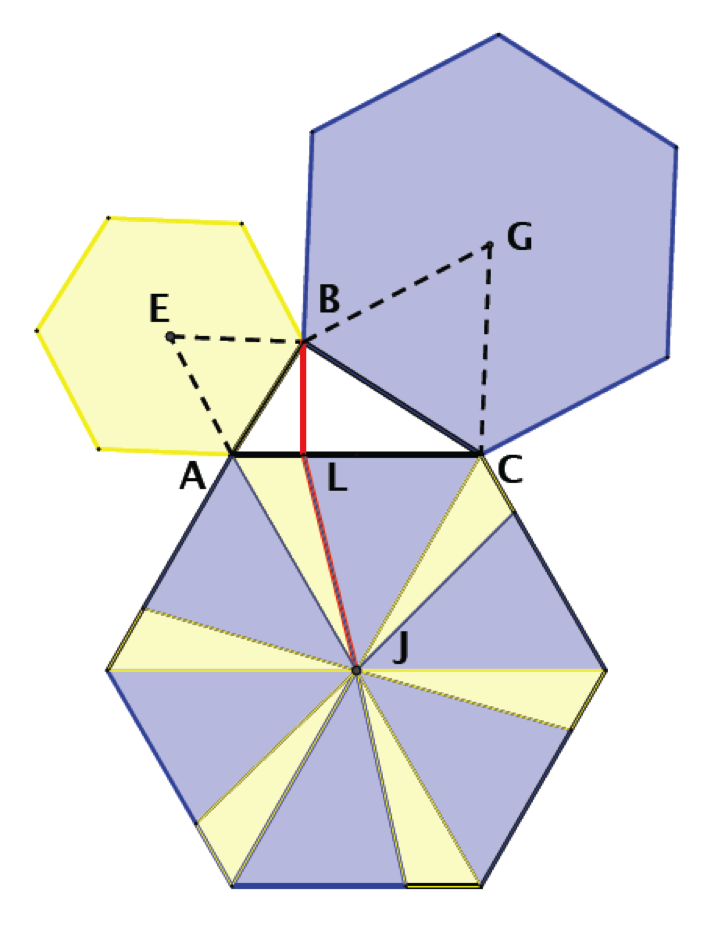
Figure 10: Regular hexagons on the sides of a right triangle. Line segment LJ, shown in red, is one of six line segments forming a sort of generalized Pythagorean cut.
Can the hexagon on AC be divided into two parts each having area equal to that of one of the hexagons on AB and BC? Knowing how to divide triangles in this way gives us a way to divide the hexagon on AC into two sets of six pieces each, so that the areas of the pieces in each set add up to the area of the hexagon on AB or BC. If BL is perpendicular to AC, we know that LJ is a Pythagorean cut for equilateral triangle AJC, so that the area of triangle ALJ equals the area of triangle AEB. Marking off a segment equal to AL on each side of the hexagon with center J ensures that the sum of the areas of the triangles shaded in yellow in hexagon J will equal the area of the hexagon E. Consequently, since the area of triangle LCJ equals the area of triangle BCG, the sum of the areas of the triangles shaded in blue in hexagon J must equal the area of hexagon G. Thus,
area of hexagon J = area of hexagon E + area of hexagon G.
In this way, the Pythagorean cut can be replicated to ensure that the n-gon on the hypotenuse is subdivided into two collections, each consisting of n congruent triangles, such that the sum of the areas of the triangles in each collection equals the area of one of the two smaller n-gons. Please note that although the basic triangle for the hexagon is an equilateral triangle, the Pythagorean cut described above will hold for any isosceles triangle and thus for any regular n-gon.