Impacts of a Unique Course on the History of Mathematics in the Islamic World
Overview
I have been teaching a new and quite unique course on the History of Mathematics in the Islamic World for a general liberal arts audience for the past few years. What I have learned in the process has been transformational for myself and highly surprising and influential for my students. This article discusses several aspects of the course and its impacts on the instructor, students who have taken the course, and others.
Introduction
The idea that I teach a course on the History of Mathematics in the Islamic World at Kenyon College in Gambier, Ohio, originated from a colleague outside my department. Having no training in the history of mathematics, my reaction was “this is a great idea, but I hardly know anything about it. I would first need to learn the subject before I could teach it.” I am so grateful to this colleague because her suggestion has been profoundly influential and transformative in my intellectual and academic life. The course also has had a similar impact on many of the students who have taken it. Additionally, a larger audience has learned about the subject from the lectures the author has given during the last few years in many different venues, including community centers, departmental colloquia at colleges and universities, and international meetings. My students also gave presentations at a community center to help inform the general public on the subject.
Some of the most fundamental notions of modern mathematics and science are a legacy of the medieval Islamic civilization (see Note). Although current research is far from giving us a full account of their contributions, we know that this legacy includes the number system that we use today, the fields of algebra and trigonometry, the concept of algorithm, the foundations of optics, the scientific method, and important works in astronomy that played a crucial role in the Copernican revolution. Yet, these contributions are generally little known, not only in the West, but also in the Islamic World. Moreover, there are widely held misconceptions about the nature of scientific contributions from the Islamic civilization. The new course I began teaching at Kenyon College is an attempt to increase awareness about contributions to the development of modern science from the medieval Islamic civilization, and to address some of these misconceptions based on evidence and research.
Note: I will be using the terms “medieval Islamic civilization” and “Islamic civilization” in a very broad sense. We are particularly referring to the medieval Islamic civilization for which the time period goes approximately from the late 7th century to the 16th century (inclusive). Geographically, this civilization spanned a large region – from Spain in the west to China and India in the east. Therefore, it encompassed much diversity in terms of languages, ethnicity, and cultures. It also included many different political powers and entities, such as Umayyad, Abbasid, Fatimid, al-Andalus, Seljuk, Ottoman, Safavid, and many others. It was ethnically and religiously highly diverse. Individuals from many different backgrounds contributed to scientific knowledge and progress; being a Muslim was not a prerequisite for this contribution. Arabic was the language of science during this time period, and it has been the language of religious studies. Again, we use the terms “medieval Islamic civilization” and “Islamic civilization” in a very broad sense, and in no way do we mean to imply a monolithic civilization or culture.
Impacts of a Unique Course on the History of Mathematics in the Islamic World - Initial Challenges and the Design of the Course
Kenyon College is a small liberal arts college, so the course I designed, History of Mathematics in the Islamic World, needed to appeal to a general liberal arts audience. General History of Mathematics courses at the undergraduate level are common across colleges and universities in the U.S., but I have not seen an introductory history of mathematics course that focuses on the Islamic world. Finding suitable textbook(s) was a real challenge. Fortunately, I came across J. Lennart Berggren’s Episodes in the Mathematics of Medieval Islam [2] (suggested by experts) for the mathematics content of the course. I also chose George Saliba’s Islamic Science and the Making of the European Renaissance [22] for the history and social science aspects of the course. I usually spend one day discussing Bradley Steffens’ book, Ibn al-Haytham: First Scientist [25], written for a general audience with useful information for the students in the course.
 |
 |
Figure 1. Left: Cover of the book, Ibn al-Haytham: First Scientist, by Bradley Steffens. Right: Title page of a Latin translation of Ibn al-Haytham's (Alhazen's) Optics, published in Basel, Switzerland, in 1572 (courtesy of History of Science Collections, University of Oklahoma Libraries). A complete copy of this book can be viewed online courtesy of ETH-Bibliothek Zürich via e-rara: http://dx.doi.org/10.3931/e-rara-9817.
Abu Ali al-Hasan ibn al-Haytham (965-1040), commonly known as Alhazen in the west, is one of the giants of Islamic science. He is known as the father of optics; however, his main contribution to science was introducing the experimental method into scientific inquiry in a systematic way. His work in optics is connected to a well-known geometry problem known as Alhazen’s problem in the literature, as well as to ideas of integral calculus ([10], [17]).
I have taught the course, History of Mathematics in the Islamic World, a few times since Spring 2011. The audience has been overwhelmingly general liberal arts students with very few majors in mathematics or natural sciences. It fulfills my college’s quantitative reasoning requirement, and it contributes to the Islamic Civilization and Cultures program which was recently established at Kenyon. About 60-65% of the course is devoted to mathematical content from Berggren’s text [2], and the rest is history and social science content, mainly from Saliba's book [22] with some additional supplementary materials. A weekly outline of the material discussed in the course is as follows.
| Week 1 | Overview and Introduction. Lives and works of selected Islamic scholars: Al-Khwārizmī, Al-Biruni, Omar al-Khayyám, Al-Kāshī, Ibn al-Haytham | |
| Weeks 2-3 | Islamic Arithmetic (Berggren Chapter 2) Reading and Class Notes Guide: Sections 2.3 & 2.4 Reading and Class Notes Guide: Section 2.7 |
|
| Weeks 4-5 | Geometrical Constructions in the Islamic World (Berggren Chapter 3) Reading and Class Notes Guide: Section 3.4 |
|
| Week 6 | Midterm Exam I, Saliba Chapters 1 & 2 Saliba Ch. 1: The Islamic Scientific Tradition: Question of Beginnings I Saliba Ch. 2: The Islamic Scientific Tradition: Question of Beginnings II |
|
| Week 7 | Saliba Chapters 2 & 3 Saliba Ch. 3: Encounter with the Greek Scientific Tradition |
|
| Weeks 8-9 | Algebra in Islam (Berggren Chapter 4) Reading and Class Notes Guide: Section 4.4 |
|
| Weeks 10-11 | Trigonometry in Islam (Berggren Chapter 5) | |
| Week 12 | Midterm Exam II, Saliba Chapter 4: Islamic Astronomy Defines Itself: The Critical Innovations | |
| Week 13 | Saliba Chapters 5-7, selected additional readings Saliba Ch. 5: Science between Philosophy and Religion: The Case of Astronomy Saliba Ch. 6: Islamic Science and Renaissance Europe: The Copernican Connection Reading and Class Notes Guide: Chapter 6 Saliba Ch. 7: Age of Decline: The Fecundity of Astronomical Thought |
|
| Week 14 | Presentations of final projects |
Mathematical content constitutes the larger part of the course (about 60-65%) and it is challenging for this audience. As an additional resource for the students, I created several video lessons on selected topics from Berggren’s text [2]. They are publicly available on the course website: http://www2.kenyon.edu/Depts/Math/Aydin/Teach/Fall14/128/index.html. An innovative element I introduced to the course is a community service component, which is described later in this article.
I often use handouts for daily class activities (sometimes supplemented by PowerPoint presentations) to help students organize their notes and identify major points in each section. A sample of a few of these handouts are included for download in the schedule above.
In lieu of a final exam, students do a final project in this course on a topic of their choice. Many potential ideas and resources are suggested, but students are free to choose a different topic, subject to the approval of the instructor. The most popular topic has been mathematics – and geometry in particular – in Islamic art and architecture. There are many aspects of this topic for students to explore, including:
- constructions of Islamic geometric patterns,
- Islamic influence on European architecture,
- mathematics of mosques,
- geometry of muqarnas, and
- geometry of Kufic calligraphy.
Some other examples of topics students have chosen for their final projects include:
- contributions of particular Islamic scholars to mathematics and sciences, including Ibn al-Haytham, Jamshid al-Kāshī, Omar Khayyám, and Thābit ibn Qurra,
- the Alhazen problem,
- cryptology in the Islamic world,
- the Qibla problem,
- astronomy in the Islamic world,
- number systems and numerical approximations, and
- mathematical geography and cartography.
The list of potential topics and resources is very large and it continually grows. The final project gives students the chance to explore a topic they are interested in but we did not have time to discuss in class, or go deeper into a topic that was briefly discussed in class.
More details about the course, including the course syllabus, actual daily calendar, homework and reading assignments, exam dates, links to publicly available video lessons, information and resources for the final project, and links for additional resources can be found on the course web site from Fall 2014: http://www2.kenyon.edu/Depts/Math/Aydin/Teach/Fall14/128/index.html
Once again, the textbooks I have used in my History of Mathematics in the Islamic World course thus far are:
- J. Lennart Berggren’s Episodes in the Mathematics of Medieval Islam [2];
- George Saliba’s Islamic Science and the Making of the European Renaissance [22]; and
- Bradley Steffens’ Ibn al-Haytham: First Scientist [25].
In addition to the second edition of Berggren’s Episodes in the Mathematics of Medieval Islam, published in 2016 [3], there are a few other textbooks that could be used for a course on the History of Mathematics in the Islamic World. For instance, one could use selections from:
- Victor Katz’s A History of Mathematics: An Introduction [11];
- Katz’s and Karen Parshall’s Taming the Unknown: A History of Algebra from Antiquity to the Early Twentieth Century [12];
- Katz’s Sourcebook in the Mathematics of Egypt, Mesopotamia, China, India, and Islam [13a], especially the chapter contributed by Berggren, “Mathematics in Medieval Islam,” pp. 515-675; and/or
- Katz’s Sourcebook in the Mathematics of Medieval Europe and North Africa [13b], especially the chapter contributed by Berggren, “Mathematics in the Islamic World in Medieval Spain and North Africa,” pp. 381-547.
The Convergence article, "Combining Strands of Many Colors: Episodes from Medieval Islam for the Mathematics Classroom" [24], presents several modules on Islamic mathematics that would be very useful for instructors interested in incorporating this material into their courses.
Impacts of a Unique Course on the History of Mathematics in the Islamic World - What I Learned and Impact on My Scholarship
I started learning about the material for my History of Mathematics in the Islamic World course from scratch. I was truly fascinated but also deeply disappointed by what I learned. I quickly realized that, despite new discoveries in recent decades, the research in the field is highly incomplete. This was stated by virtually every expert in the subject, most of whom are western researchers. (See the Note below for quotations on this topic from experts in the field of Islamic mathematics.) Worse still, there are many widespread misconceptions and exaggerations and much simply false information on the subject. This is the case not only in the west but also in the Islamic world as well. This unfortunate state of affairs can be largely attributed to what Saliba called “The Classical Narrative.” As a person who was born and raised in the Muslim majority country of Turkey and spent about half of his life in the U.S., Saliba’s description of the classical narrative resonated strongly with me as I witnessed it in so many different ways and places; from my home country to the local school district in rural Ohio, to textbooks on history of mathematics or science.
The details of the classical narrative can be found in Saliba’s Islamic Science and the Making of the European Renaissance [22], but in essence it is a certain way of describing the nature of scientific activities in the Islamic civilization which is based not so much on evidence or documentation, but rather on some preconceived ideological assumptions. It belittles the contributions to science from the medieval Islamic civilization, and views the preservation of the ancient Greek scientific heritage through translations as the main contribution of the Islamic civilization. Thus, according to this view, the role of the Islamic civilization was to serve essentially as a refrigerator for Greek ideas. It downplays or overlooks many fundamental and original contributions to mathematics and science from the Islamic civilization, and its influence on Renaissance Europe. For example, connections between Islamic scholars such as Nasir al-Din al-Tūsī (1201-1274) and ʿAlāʾ al‐Dīn ʿAlī ibn Ibrāhīm ibn al‐Shāṭir (c. 1305-1375) and Renaissance scholars such as Nicolaus Copernicus (1473-1543) are largely unknown ([20], [7]).
As a person who grew up in Turkey, I can attest that the classical narrative seems to be widespread in the Islamic world as well. As a result, the view that modern science is a western phenomenon [18] with ancient Greek origins and a revival in Renaissance Europe is common. Few people know about the significant and fundamental original contributions to science from the Islamic civilization. On the other extreme of the spectrum, there are people who have heard about some of the Islamic contributions to science, but they lack accurate knowledge and tend to exaggerate these contributions. One common misconception of this sort is the idea that Muslims first invented zero.
To be fair to the general public, even the researchers missed some of the fundamental facts in the field. For example, the invention of decimal fractions had been incorrectly attributed to Simon Stevin for a long time [15], and the connections between Copernicus and earlier Islamic scholars were not known until the second half of the 20th century ([20], [7]). Research in more recent decades has provided a wealth of outcomes that challenge, contradict, or disprove the classical narrative, but it takes more than articles in specialized academic journals to remedy the damage caused by this narrative. For example, after studying the work of Copernicus and earlier Islamic scholars closely, Noel Swerdlow and Otto Neugebauer came to the conclusion in 1984 that “[i]n a very real sense, Copernicus can be looked upon as, if not the last, surely the most noted follower of the Maragha School” [27, p. 295]. This is a vastly different assessment than the one the classical narrative proposes.
To return to another example, although researchers realized in the mid 20th century that decimal fractions were invented and systematically treated many centuries before Stevin (1548-1620) in the Islamic world ([21], [15]), a popular book published in the 21st century still claims that Stevin was the first inventor [6]. A Nobel Laureate repeats this false claim in the foreword (page xiii):
The decimal system is so familiar to us that one might forget that it actually had to be invented by someone. This someone also had to find out how to add, subtract, multiply and divide such numbers. His name is Simon Stevin, ….
Therefore, there is a need to disseminate the results of established research to the general (educated) public. This is in addition to the great need to study the vast amount of original scientific material from the Islamic world that has not yet been examined by modern scholars. Expert after expert acknowledges that the research in this field is highly incomplete. (See the Note for details.)
It is encouraging that a considerable amount of research has been done in the field of Islamic mathematics in recent decades. For example, survey articles by Berggren [4] and Glen Van Brummelen [29] give a summary of recent research through 2011. Still, much research remains to be done (again, see the testimonials in the Note below). Also, as noted above, there is still a large gap between what specialists know and what the (educated) general public knows that needs to be closed. The classical narrative is so widespread and has been around for so long that it will take time and effort to disseminate research findings in the field and change perceptions. This means it is important that contributions from the Islamic civilization be mentioned by those in the know when the history of certain topics in mathematics is discussed or taught. For example, a recent article in Convergence [5] that focuses on Stevin's work as a tool for helping future teachers understand multiplication of decimal fractions seems to me to have missed an opportunity to educate the larger community about the development of decimal fractions by Islamic mathematicians. One wishes the author had noted the highly relevant facts that Abu'l Hasan al-Uqlīdisī wrote about decimal fractions in around 952 in the city of Damascus [21] and Jamshīd al-Kāshī, a leading mathematician and astronomer at the observatory in Samarkand, presented a systematic treatment of decimal fractions in the year 1427 ([2], [3], [15]).
The History of Mathematics in the Islamic World course is an attempt to fill the gap between what academic researchers have discovered and what the educated public knows. The purpose of the course is not to promote the achievements of a particular culture. It is about understanding the history of mathematics better. It is true that we focus on the Islamic world; this is because it is an area that has been long neglected and misconceptions have caused a lot of damage to our understanding of the history of science. Moreover, there have been interesting and exciting discoveries by modern historians of science that are not yet widely known among the educated public. Without understanding what happened in the Islamic world, one really does not understand European history, or the history of mathematics more generally. As Saliba stated in Islamic Science and the Making of the European Renaissance ([22], p. ix), “I must quickly caution those readers [readers who feel a sense of kinship with the Islamic civilization] not to read this book as an expression of greatness of the Islamic scientific tradition ….” The goal instead is to understand global history of science better by studying history of Islamic science and disabuse ourselves of common misconceptions.
Given this state of affairs and my interest in the subject, I felt as if I needed to make a contribution. For this purpose, being able to read original documents, hence a reading knowledge of classical Arabic, was necessary. I spent a considerable amount of time studying Arabic, taking Arabic courses at Kenyon and attending a summer language program in Jordan. Then I started a major translation project in collaboration with a colleague from another institution in Ohio. We are translating from Arabic to English Al-Kāshī’s Miftāh Al-Hisāb, one of the most important mathematics books of the medieval Islamic civilization. Berggren described it as the “crowning achievement of Islamic arithmetic” ([3], p. 22). We have made significant progress in the translation project but there is still a long way to go. We published our first article related to the translation project in 2015 in Archive for History of Exact Sciences [1]. My work in studying Arabic and starting the translation project has been supported by two grants from the Great Lakes Colleges Association (GLCA) New Directions Initiative. As a result, a totally new area of research and teaching has been added to my professional life. Before talking to my colleague at Kenyon College who proposed the idea of the new course, I had no plans or intentions to start working in this field. I consider this experience to be a good example of the commitment to life-long learning and broad education that we would like to promote for our students, particularly at liberal arts colleges.
Note: Experts agree that much work remains to be done on the history of Islamic mathematics. Testimonials from some of these researchers follow.
I have not attempted to write "The History of Mathematics in Medieval Islam". Such a book could not be written yet, for so much material remains unstudied that we do not know enough of the whole story. – J. L. Berggren, in Episodes in the Mathematics of Medieval Islam ([2], page viii)
Clearly the field still offers an abundance of material for further investigation, and there is much work yet to be done. – J. L. Berggren ([4], page 91)
A complete history of mathematics of medieval Islam cannot yet be written, since so many of these Arabic manuscripts lie unstudied and even unread in libraries throughout the world. The situation has been improving recently as more and more texts are being edited and translated, but political difficulties continue to block access to many important collections. Still, the general outline of mathematics in Islam is known. In particular, Islamic mathematicians fully developed the decimal place value number system to include decimal fractions, systematized the study of algebra and began to consider the relationship between algebra and geometry, brought the rules of combinatorics from India and reworked them into an abstract system, studied and made advances on the major Greek geometrical treatises of Euclid, Archimedes, and Apollonius, and made significant improvements in plane and spherical trigonometry. – V. Katz, in A History of Mathematics: An Introduction ([11], page 267)
The historian of the Islamic exact sciences is frequently confronted with an embarras de richesse – hundreds of manuscript sources which have never been studied in modern times. – E. S. Kennedy, "Islamic Mathematical Geography," in Studies in the Islamic Exact Sciences (1983), page 18.
Today, even in the Islamic World, their activities and achievements have been completely forgotten …. Virtually all of the materials presented in this book have never been researched before in modern times. – David A. King, in In Synchrony with the Heavens: Studies in Astronomical Timekeeping and Instrumentation in Medieval Islamic Civilization (2004), page ix
Impacts of a Unique Course on the History of Mathematics in the Islamic World - Some Pedagogical Aspects
Anyone who studies the history of mathematics realizes that the way we teach mathematics is often misleading. Historically, new mathematical material is rarely discovered in the way it is presented in textbooks. When the teachers do not know about the history of the material well enough to explain the way mathematics was originally developed (when the details of the historical development are known, which is not always the case), some valuable pedagogical dimensions are lost. I would like to give a few examples that show the disconnect between historical development and teaching practice.
Today, when they hear the term algebra, most students probably think of symbols (such as x, y, and z) and their manipulations. However, for many centuries algebra was done completely in prose (except that sometimes geometry and geometric figures were used to explain or justify algebraic procedures). The introduction of symbolism into algebra is a much later phenomenon ([8], [28], [12]). Hence symbol manipulation is not the essence of algebra. As teachers of mathematics we need to better explain what the main idea is in algebra. As Al-Samawʾal explicitly stated and Omar Khayyám further explained, algebra is operating on the unknown quantities in the same way you operate on the known quantities, and using the relations between the known and the unknown quantities to determine the unknown quantities. Knowing the historical development is relevant and helpful.
The method of “completing the square” is a standard one in the modern school curriculum. We often teach it as a purely algebraic procedure to manipulate and solve quadratic expressions or equations (by extension, possibly higher degree expressions as well). Historically, however, it was based on the geometry of squares, rectangles, and L-shaped figures formed from them, which together represented quadratic expressions and equations. In the example below, we'll show how Thābit ibn Qurra (836-901) used a geometry theorem stating that an L-shaped geometric figure has the same area as a square to transform a quadratic equation we would write as \(x^2 + m = nx\) into the form \[m+\left(x-\frac{n}{2}\right)^2 = \left(\dfrac{n}{2}\right)^2,\] thereby making it easier to solve. Since the general idea of this method was to replace L-shaped figures by squares, perhaps it would be more accurate to call the method "converting to the square."
Early Islamic scholars, who were pioneers of algebra, used the idea of "completing the square" or "converting to the square" to justify their procedures to solve quadratic equations. Rigorously established geometry theorems from Euclid's Elements formed a solid foundation for their approach. For example, Thābit ibn Qurra’s use of Propositions 5 and 6 from Book II of the Elements in justifying solutions to quadratic equations is described in Berggren's text ([2], pages 104-107). It is unfortunate that many teachers and students miss out on this connection between geometry and algebra that was historically well established.
Euclid's Elements, Book II, Proposition 5. If a line AE is divided at B and bisected at W, then the rectangle AB x BE plus the square on BW is equal to the square on AW.
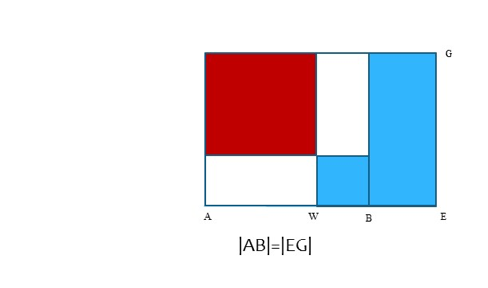
Figure 2. The diagram above illustrates Proposition 5 of Euclid's Elements. Under the given hypotheses, the area of the L-shaped blue region is equal to the area of the red square.
For more details on Euclid's Elements, Book II, Proposition 5 and Proposition 6, see David Joyce's presentation of the text at his website: http://aleph0.clarku.edu/~djoyce/java/elements/.
Ibn Qurra used Proposition 5 to solve one type of Al-Khwārizmī’s quadratic equations; namely, the quadratic equation that we would write as \(x^2 + m = nx,\) where \(x,\) \(m,\) and \(n\) are positive.

Figure 3. The diagram above illustrates the application of Proposition 5 to the solution for \(x\) of the quadratic equation \(x^2 + m = nx,\) where \(x,\) \(m,\) and \(n\) are positive. By Proposition 5, m + |BW|2 = |AW|2. Since |AW| and m are known, |BW| can be found. Since |BW| = \(x - \dfrac{n}{2}\) and \(n\) is known, \(x\) can be found. Or, in more modern terms, the area equation, m + |BW|2 = |AW|2, can be written algebraically as \[m+\left(x-\frac{n}{2}\right)^2= \left(\frac{n}{2}\right)^2,\] and solved for \(x.\)
In the quadratic equation \(x^2+m=nx,\) \(m\) and \(n\) are known, positive quantities. In the figure above, the area of the rectangle GB is \(m.\) One side of the largest rectangle is of length \(n\) (hence known), the other side is of length \(x\) (hence unknown). The length of segment AB is also \(x,\) where \(n> x\) and, in this case, \(x> \dfrac{n}{2}.\) Therefore, the figure represents the equation \(x^2+m=nx\) (since each side of the equation is the area of the largest rectangle).
Now we apply Proposition 5. First note that since \(n\) is known and W is the midpoint of segment AE, the length of segment AW is known to be \(\dfrac{n}{2}.\) Consider the L-shaped blue region. Its area is \[m+\left(x-\frac{n}{2}\right)^2.\] By Proposition 5, its area is also equal to \(\left(\dfrac{n}{2}\right)^2.\) Thus, we obtain the equation \[m+\left(x-\frac{n}{2}\right)^2 = \left(\dfrac{n}{2}\right)^2.\] Therefore, the original equation \(x^2+m=nx\) is transformed to \[m+\left(x-\frac{n}{2}\right)^2= \left(\frac{n}{2}\right)^2\] by Proposition 5. This is precisely what we get when we “complete the square” in the equation \(x^2+m=nx\) in a purely symbolic way.

Figure 4. The page above is from a manuscript copy of Al-Khwārizmī's Al-Jabr. For details of how the square is completed by filling in its four corners, see "Mathematical Treasures - Al-Khwarizmi's Algebra" here in Convergence. (Source: Columbia University Libraries)
Today, algebra is arguably the most important branch of modern mathematics as evidenced by the fact that one can take almost any subfield of modern mathematics and stick the adjective "algebra" in front of it and there turns out to be such a discipline; for example, algebraic geometry, algebraic number theory, algebraic topology, algebraic coding theory, algebraic combinatorics, and many others. It is really interesting to trace the origins of the point of view that made algebra such a powerful tool in modern mathematics. When we study the works of Omar Khayyám (1048-1131), one of the great mathematicians of medieval Islam who is better known as a poet, we find some hints. Al-Khwārizmī (780-850), an earlier and possibly better known Islamic mathematician, wrote the first known algebra book in history, copies of which survive (see Notes 1 and 2). From the title of this book, we get the English word algebra as a transliteration of the Arabic “al-jabr” ( الجبر ) [19], and Al-Khwārizmī's own name became the term algorithm over the ages. While Al-Khwārizmī classified and solved quadratic equations in a systematic way, Omar Khayyám did the same for cubic equations. One major difference between the works of the two scholars was the following: al-Khwārizmī studied quadratic equations systematically and presented numerical recipes (“algorithms”) to solve them, whereas Khayyám could only solve cubic equations in purely geometric ways. That is, his solution to a particular problem would be a geometric quantity such as the length of a line segment obtained after a sequence of geometric constructions, some involving only Euclidean tools and others requiring conic sections. Khayyám acknowledged that he failed to find numerical solutions to cubic equations like Al-Khwārizmī did for quadratic equations, and he hoped that mathematicians after him would succeed in doing so. Indeed, his wish was fulfilled some four centuries later. Despite this shortcoming, his view of algebra was remarkably similar to the modern view. We can see that his work contained the seed of the huge tree that we have in modern mathematics when we read his words (quote from [2], pages 123-124):
Algebra. By the help of God and with his precious assistance I say that algebra is a scientific art. The objects with which it deals are absolute numbers and (geometrical) magnitudes which, though themselves unknown, are related to things which are known, whereby the determination of the unknown quantities is possible … What one searches for in the algebraic art are the relations that lead from the known to the unknown, to discover which is the object of algebra …
As Berggren pointed out, if these relations happen to come from geometry, the problem is no less algebraic in Khayyám’s view. The main idea of algebra, according to Khayyám, is to use relationships between known and unknown quantities to figure out the unknown(s). It does not matter where those quantities come from. They need not be numbers or numerical values. Today, we can appreciate the value of Khayyám’s work and his point of view in a deeper way.
A recent article in Convergence, "A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation" [14], illustrates Khayyám’s method of solution to cubic equations using GeoGebra and provides more information about his work and the history of cubic equations.
 |
 |
Figure 5. Left: Muhammed ibn Musa al-Khwārizmī (circa 780-850) was the author of the earliest known book in history in which the term algebra was used as a technical mathematical term. Moreover, his name is the source of the term algorithm, a fundamental notion in modern computing. His contributions to astronomy were acknowledged by the naming of a crater on the moon after him. (Source: Wikimedia Commons)
Right: Statue of Omar Khayyám (1048-1131) in Nishapur, Iran (photographed by Muhammad Mahdi Karim, December 2011. Source: Wikimedia Commons, licensed under GFDL 1.2)
I recently realized from a computer programming textbook ([23], page 14) that the term algorithm had a much narrower meaning historically than it does today, referring originally to procedures to solve algebraic or numerical equations. (Incidentally, I had been teaching computer programming using [23] as a textbook for many years before I began teaching the History of Mathematics in the Islamic World course, but the note there did not capture my attention before.) As noted above, the term algorithm comes from Al-Khwārizmī’s own name and the term algebra from the title of Al-Khwārizmī’s algebra text. Thus, two fundamental terms of modern science come from the same source. Al-Khwārizmī gave recipes, or procedures, to solve quadratic equations in [19], effectively the quadratic formula but entirely in words. Hence, one might be tempted to conclude that his algebra text was the reason why both terms came from the same scholar. But it turns out that it is his work in another area that explains why the term algorithm is associated to his name. Al-Khwārizmī wrote one of the earlier books in the Islamic civilization that introduced the decimal system from India. The original Arabic text is lost but a Latin translation is extant. The first word of the title of the Latin translation of that book, Algoritmi de numero Indorum (Al-Khwārizmī on the Indian Numbers), gave rise to the word algorithm ([16], where the authors translate the title as Al-Khwarizmi on the Hindu Art of Reckoning). Unfortunately, many students and teachers are not aware of these connections.
Note 1. We are fortunate to have copies of Al-Khwārizmī’s original text in algebra in Arabic, which has been translated to English. Unfortunately, a great many historical scientific books are lost.
Note 2. There were certainly works in earlier civilizations that can be considered as algebra, but scholar of Islamic mathematics Roshdi Rashed classified Al-Khwārizmī’s book as “a foundation text for algebra, since it is the work in which algebra was, for the first time in history, conceived as a mathematical discipline independent of geometry and of arithmetic” [19].
Impacts of a Unique Course on the History of Mathematics in the Islamic World - Impacts on Students and the Larger Community
Most of the students who have taken the History of Mathematics in the Islamic World course say that it has been an eye-opening course and they are extremely surprised and saddened that they had never heard of such great contributions to mathematics and the sciences from the Islamic civilization before taking the course. Some of the students stated (in final reflection papers at the end of the semester and course evaluations) that they could not help but communicate what they learned in this course to family members or high school teachers. I have had students contact me to discuss matters related to the content of the course after graduating from college. It is evident that the course was deeply enlightening for many students and had a profound and long-lasting impact on them.
The following comments from two students, one from each of two different offerings of the course, are more detailed than most, but typical in other ways. Notes [in brackets] have been inserted by the author for clarification.
Student A, from Fall 2013:
When I first came to Kenyon, I remember perusing the course listings, eager to begin my “liberal arts journey.” Upon seeing “History of Mathematics in the Islamic World,” I knew this was one course my other friends attending big universities would never have the opportunity to take…..
When I went home for Thanksgiving Break I couldn’t help but explain the misconceptions of Copernicus, innovations of Al-Khwārizmī, and various talents of Omar Khayyám. I’m not sure if my family completely understood everything I explained, but I was just so eager to share with them my newly acquired knowledge.
If my goal in signing up for this course was to truly experience the essence of a liberal arts education, I know I have succeeded. I’m grateful for making the decision to take this course because it has been enlightening in so many ways, and I hope I can [convey] this enlightenment to others in the future.
Student B, from Fall 2011:
Overall, this class has corrected many of the misconceptions that I have had on the contributions of Islamic mathematicians and scientists. My freshman year of high school, in my World History class, my final project was a debate over whether the Tang Dynasty or the Abbasid Dynasty was more influential. Though I was debating on the side of the Tang Dynasty, I remember many of my opponents’ arguments. As a conclusion for my reflection paper, I would like to include an email I sent to my high school history teacher, which I felt compelled to write after taking this class: …..
One innovative element I tried in the course was a community service component. Since most of the Muslim community is not aware in an accurate way of the historic contributions of Islamic civilization to modern science, I thought it would be useful for the Islamic community to hear final presentations from my students at the end of the semester. In lieu of a final exam for the course, students do a final project which has two components, either an oral presentation or a poster, and a paper. For the first few offerings of the course, students always presented their projects to the class. In Fall 2014, I arranged for them to present at an Islamic community center in Columbus, Ohio, which is about one hour away from the Kenyon College campus. Despite some difficulties in logistics, it was a successful and useful experience for both the students in the class and the local community in central Ohio. Feedback from both students and audience members about this experience follows.
Comments from students who participated in the event at the Community Center (December 14, 2014):
I thought that the presentations in Columbus went really well. I was happy with my classmates’ findings. I thought that the audience found the work engaging, which made me feel good. Sometimes, when you are just working on a project in isolation, you can’t really tell if other people are going to like what you are saying, or even understand it fully. However, I thought that everyone in the class did a good job in making the material relatable. Also, the responses from the audience were heartwarming. A lot of the things we do in classes, here at Kenyon, don’t seem like they are all that applicable outside the walls of academia. This made it seem like the research we were doing was useful for people who weren’t college students. I wish Kenyon gave more opportunities to engage with the general public.
The most rewarding aspect of the class was being able to present our final projects at the Noor Islamic Center. My partner and I had worked extensively on the project and we were thrilled to finally be presenting to an audience at the Center. I respect the members of the Islamic Center immensely and I was completely elated when one member had come up to me and asked me to write down some terms from our presentation so that she could look them up later. In fact, many individuals had come up to me and thanked me for teaching them something that they had little prior knowledge [of]. It was amazing how invested they were in what we had worked on and how open they were with their gratitude. Truthfully, it was I that was most grateful. It was so uplifting that the Center had wanted us to come all the way from Gambier to give our presentations. It was in the moments [preceding] our presentations in which everyone [was] conversing and thanking us, that everything that I had worked for in the course had come together. I became vehemently proud of my work in the course and confident of the knowledge I had acquired. This class has taught me many things that will carry on through my academic career, as well as beyond my schooling.
I think the presentations organized for us at the NICC at the end of this semester put an extra emphasis on the importance of what we’ve learned this semester. Besides having the opportunity to present our findings to a community to whom our course applies heavily, it was fantastic to hear their pleasure at listening to our presentations at the end of the event. My main problem with science and mathematics courses in my life has been my inability to see how they apply to the world I live in, but due to the cultural component in this course that was no problem at all. I also think the trip to the Mosque at the beginning of the semester was integral to my appreciation of these presentations at the end.
Our final trip to the NICC was really enjoyable. It was really fulfilling to see all of the community members so genuinely interested in our presentations. I felt as if we actually shared something valuable that they did not know before, which made me glad.
After our group’s final project presentation at Noor Islamic Culture Centre in Columbus, I met an Iraqi community member who echoed my response to the material I learned in this class. The woman explained to me that she was interested in the intellectual history of the Middle East. Having attended secondary school and higher education [university] in Iraq, she studied a very basic introduction to the general interests of scholars such as Ibn al-Haytham and al-Khwārizmī. Both Islamic scholars were either Iraqi or lived much of their lives in Iraq. However, the woman explained that she had not learned the specific technical details of these scholars’ works. Prior to taking this class, I knew the broad areas of interest certain popular Islamic scientists entertained. For instance, I knew that al-Khwārizmī invented algebra and Ibn Sina was an anatomist and expert physician. The Iraqi woman and I agreed that prior to exposure to this class we did not know specific technical details of the Islamic scholars’ scientific output. Whereas both the Iraqi woman and I knew specific details of Isaac Newton’s gravitational theory, we did not know much on the specific scientific content of the scholars.
It was very rewarding to go to the cultural center and present. All the talks were very good, and, even though we didn’t get to properly present [some groups had posters, others gave talks], it actually worked very well. It meant that our entire presentation was more personal, and we interacted with a lot of people. It was nice to get to talk to people about our project. Even though we got back a little late, it was still very fun and it was nice to get to go to the cultural center again.
Comments from community members who attended the presentations at the Community Center:
"All the students are so well-versed on these topics. Excellent! Thank you!"
"Thank you for coming. Wonderful presentation. Hope students can come again."
"Thank you for coming. The presentation was useful and informative. Learned a lot. I did not know about Islamic scholars & math and science."
"Tiles/rugs/art beautiful. I see tessellations in many of them."
"I really liked your presentation about math."
Impacts of a Unique Course on the History of Mathematics in the Islamic World - Our Recent Work on History of Mathematics
As mentioned above, I undertook a large translation project in collaboration with a colleague at another institution who is a mathematician and a native speaker of Arabic. We have been working on translating one of the most important mathematics books of the medieval Islamic civilization, Miftāh al-Hisāb, which can be translated as either Key to Arithmetic or Calculator’s Key, by Ghiyāth al-Dīn Jamshīd Masʿūd al-Kāshī (1380-1429), who is known as al-Kāshī or al-Kāshānī. Researchers who have studied Miftāh al-Hisāb, completed in 1427, agree that it is “the crowning achievement of Islamic arithmetic” ([3], p. 22). It has three main parts: one on arithmetic, one on geometry and measurement, and the third part on algebra. Among its many jewels are algorithms to find (approximate as rational numbers) square roots and higher order roots of integers.

Figure 6. Written in 1427, Al-Kāshī's Miftāh al-Hisāb is one of the most important mathematics books of the medieval Islamic civilization. These pages are from one of the oldest known manuscripts of Miftāh al-Hisāb, from Süleymaniye Library in Istanbul, written in 1450 (854 h.) (Source: Image used by kind permission of Süleymaniye Library, Istanbul, Turkey)
This book came to the attention of western researchers in 1948 ([15]). Prior to this date, Simon Stevin (1548-1620) was widely assumed to be the first inventor of the decimal fractions. However, Miftāh al-Hisāb contains a systematic treatment of the decimal fractions. Still, it was not al-Kāshī who first introduced decimal fractions. According to the best available research and original sources, decimal fractions were first introduced in the middle of the tenth century, almost five centuries before Al-Kāshī and over six centuries before Stevin, by the scholar Abu'l Hasan Ahmad ibn Ibrahim al-Uqlīdisī (920-980), known as Al-Uqlīdisī, in his book Kitab al-fusul fi al-Hisāb al-Hindi (The Book of Chapters in Indian Arithmetic), which has been translated into English [21].
The story of modern researchers’ understanding of the origin of decimal fractions is highly instructive, showing that the lack of research and lack of evidence from original sources can lead to an incorrect understanding of the history of mathematics. Furthermore, once misconceptions are widely circulated, it is then very difficult to correct them, as highly reputable people may repeat inaccurate information. As noted above, it takes more than scholarly articles in research journals to change the common narrative.
While our translation project is not yet complete, we noticed that the content of Miftāh al-Hisāb contains another potential connection between al-Kāshī and Stevin. We observed that Stevin also presented algorithms to find (again, to approximate) roots of integers. On the surface, the procedures by al-Kāshī and Stevin look very different. A close examination of their work, however, reveals that they actually used the same underlying algorithm. The details are described in our recent paper [1]. We also observed that Stevin’s procedure contains a flaw and does not always work. Moreover, he did not seem to understand the rationale behind at least one step in his algorithm, hence did not seem to have a full understanding of the algorithm he presented. So far, to the best of our knowledge, nobody has established a link between the two scholars, but, based on these observations, we wonder if there was any direct or indirect connection between Al-Kāshī and Stevin. Like many other questions in the history of science (such as if and how Copernicus came to know of the works of earlier Islamic scholars such as ibn Shātir and al-Tūsī [20], [7]), this is an open question at the moment.
An alternative method of approximating square roots of integers by a 12th century Islamic scholar, Abu Bakr al-Hassar, with the flexibility of improving the accuracy of approximation by increasing the number of iterations, is presented in the Convergence article, "Extracting Square Roots Made Easy: A Little Known Medieval Method" [9].
Impacts of a Unique Course on the History of Mathematics in the Islamic World - Changes to the Course and Conclusion
Changes to the Course
I plan to make a few changes to the History of Mathematics in the Islamic World course in the next offering in Fall 2017. First, there is now a long-awaited second edition of Berggren's textbook [3]. He has corrected mistakes in the first edition and added more material; notably, contributions of the western part of the Islamic world to mathematics. I plan to use the second edition [3] in Fall 2017. Steffens has written a novel about Ibn al-Haytham [26], which I plan to incorporate as well. As noted above, the final project in the course consists of two parts: a paper and a presentation. For the presentation, students have had two options: a talk or a poster. Now, I will add a third option of digital storytelling (a video). I got this idea when I attended a digital storytelling workshop recently and tried making a video that told the story of Ibn al-Haytham. I think some students will like this idea. I also plan to have students present their final projects at the Islamic Community Center in Columbus again. This time around, I will try to arrange all the logistics in summer before the semester starts.
Conclusion
Teaching this new History of Mathematics in the Islamic World course has been profoundly influential on my scholarly life and it has helped many people to better understand and appreciate a chapter in the history of science that has usually been inadequately or misleadingly represented. It is clear that there is a great need for more academic research in this field as well as a great need to disseminate available information to the general public. More of this material can and should be taught in secondary schools, colleges, and universities. If you have an interest in learning more about the subject, raising awareness about it, or offering a similar course, I would be happy to work with you.
Impacts of a Unique Course on the History of Mathematics in the Islamic World - References
[1] N. Aydin and L. Hammoudi, “Root Extraction by Al-Kāshī and Stevin,” Archive for History of Exact Sciences 69 (2015), 291-310, DOI 10.1007/s00407-015-0150-3
[2] J. L. Berggren, Episodes in the Mathematics of Medieval Islam, Springer-Verlag, 1986.
[3] J. L. Berggren, Episodes in the Mathematics of Medieval Islam (2nd ed.), Springer-Verlag, 2016.
[4] J. L. Berggren, “Mathematics and Her Sisters in Medieval Islam: A Selective Review of Work Done from 1985 to 1995 [1997],” in From Alexandria through Baghdad: Surveys and Studies in the Ancient Greek and Medieval Islamic Mathematical Sciences in Honor of J. L. Berggren (N. Sidoli, G. Van Brummelen, editors), Springer, 2014.
[5] K. M. Clark, "'In these numbers we use no fractions': A Classroom Module on Stevin's Decimal Fractions," Convergence (January 2011), DOI:10.4169/loci003333
[6] J. T. Devreese and G. V. Berghe, ‘Magic is No Magic’: The Wonderful World of Simon Stevin, WIT Press, 2008.
[7] W. Hartner, “Copernicus, the Man, the Work and Its History,” in Proceedings of the American Philosophical Society 117, no. 16 (1973): 413-422.
[8] A. Heefer, “On the Nature and Origin of Algebraic Symbolism,” Ghent University, Belgium, http://logica.ugent.be/albrecht/thesis/PMP2007Heeffer.pdf
[9] F. Katscher, "Extracting Square Roots Made Easy: A Little Known Medieval Method," Convergence (November 2010), DOI:10.4169/loci003494
[10] V. Katz, “Ideas of Calculus in Islam and India,” Mathematics Magazine 68 (1995): 163-174.
[11] V. Katz, A History of Mathematics: An Introduction (3rd ed.), Addison-Wesley, 2009.
[12] V. J. Katz and K. H. Parshall, Taming the Unknown: A History of Algebra from Antiquity to the Early Twentieth Century, Princeton University Press, 2014.
[13a] V. Katz (editor), Sourcebook in the Mathematics of Egypt, Mesopotamia, China, India, and Islam, Princeton University Press, 2007. See especially J. Lennart Berggren, “Chapter 5. Mathematics in Medieval Islam,” pp. 515-675.
[13b] V. Katz (editor), Sourcebook in the Mathematics of Medieval Europe and North Africa, Princeton University Press, 2016. See especially J. Lennart Berggren, “Chapter 3. Mathematics in the Islamic World in Medieval Spain and North Africa,” pp. 381-547.
[14] D. Kent and M. Sherman, "A GeoGebra Rendition of One of Omar Khayyám's Solutions for a Cubic Equation," Convergence (August 2015).
[15] J. J. O’Connor and E. F. Robertson, "Ghiyath al-Din Jamshid Mas'ud al-Kashi," MacTutor History of Mathematics Archive (July 1999). http://www-history.mcs.st-andrews.ac.uk/Biographies/Al-Kāshī.html
[16] J. J. O’Connor and E. F. Robertson, "Arabic mathematics: forgotten brilliance?" MacTutor History of Mathematics Archive (November 1999). http://www-groups.dcs.st-and.ac.uk/history/HistTopics/Arabic_mathematics.html (See also "Index of Islamic mathematics" and "Arabic/Islamic mathematicians in our archive in chronological order": http://www-groups.dcs.st-and.ac.uk/history/Indexes/Arabs.html.)
[17] D. Perkins, Calculus and Its Origins, Mathematical Association of America, 2012.
[18] R. Rashed, “Science as a Western Phenomenon,” in Encyclopedia of the History of Science, Technology, and Medicine in Non-Western Cultures (2008), 1927-1933. http://link.springer.com/referenceworkentry/10.1007%2F978-1-4020-4425-0_9290
[19] R. Rashed, Al-Khwārizmī: The Beginnings of Algebra (edited, with translation and commentary by Roshdi Rashed), London: Saqi, 2009.
[20] V. Roberts, “The Solar and Lunar Theory of Ibn al-Shātir: A Pre-Copernican Copernican Model,” Isis 48 (1957): 428-432.
[21] A. S. Saidan, The Arithmetic of Al-Uqlīdisī, D. Reidel Publishing, 1978.
[22] G. Saliba, Islamic Science and the Making of the European Renaissance, MIT Press, 2007.
[23] W. Savitch, Problem Solving with C++ (7th ed.), Addison Wesley, 2009.
[24] R. K. Schwartz, "Combining Strands of Many Colors: Episodes from Medieval Islam for the Mathematics Classroom," Convergence (November 2010), DOI:10.4169/loci003546
[25] B. Steffens, Ibn al-Haytham First Scientist, Morgan Reynolds Publishing, 2007.
[26] B. Steffens, The Prisoner of Al-Hakim, A Novel, Blue Dome Press, 2017.
[27] N. M. Swerdlow and O. Neugebauer, Mathematical Astronomy in Copernicus's De revolutionibus Part I, Springer-Verlag, 1984.
[28] F. R. Vallhonesta, “Algebraic Symbolism in the First Algebraic Works in the Iberian Peninsula,” Philosophica 87 (2012): 117-152. Available: http://www.philosophica.ugent.be/fulltexts/87-4.pdf
[29] G. Van Brummelen, “A Survey of Research in the Mathematical Sciences in Medieval Islam from 1996 to 2011,” in From Alexandria Through Baghdad: Surveys and Studies in the Ancient Greek and Medieval Islamic Mathematical Sciences in Honor of J. L. Berggren (N. Sidoli, G. Van Brummelen, editors), Springer, 2014.