- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Frank Morgan's Math Chat - HALES PROVES HEXAGONAL HONEYCOMB CONJECTURE
 |
June 17, 1999
Last week Professor Thomas Hales of the University of Michigan announced a proof of the Hexagonal Honeycomb Conjecture, which says that regular hexagons as in Figure 1 provide the least-perimeter way to enclose infinitely many unit areas in the plane. This may partly explain why hexagons occur in nature, as in the bees' honeycomb (but see [FT3] below). Although widely believed and often asserted as fact, even by such notables as Herman Weyl [W], this conjecture eluded proof until last week.
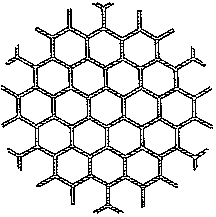
Hales proves that this hexagonal tiling provides the least-perimeter way to enclose infinitely many unit areas. From [FT2, p. 207], used by permission.
It is easy to show that the regular hexagon has less perimeter than any other hexagon of the same area. Polygons with more sides, such as a regular octagon, tending toward the circle, do better, and polygons with fewer sides, such as a square, do worse. For reasonable tilings of the plane, however, the average number of sides is at most six, and the advantage of having some polygons with more sides is less than the disadvantage of having some polygons with fewer sides. Using this fact, Fejes Tóth [FT1, FT2] proved the conjecture for polygons (with straight sides).
The second complication is that the sides can bulge in or out. Bulging out helps, while bulging in hurts. Of course if one region bulges out, the neighboring region bulges in. Hales proved that the advantage of bulging out is less than the disadvantage of bulging in. Therefore polygons are best, and regular hexagons are best of all.
The key lemma is an "isoperimetric" estimate for perimeter in terms of area, with penalties for bulging out or for more than six sides.
Actually, since the plane is infinite, one can only talk about limiting averages of perimeter per region. The proof begins with a reduction to finite clusters, which requires assuming that the regions are connected.
This is the same Hales who recently proved Kepler's Conjecture on the tightest way to pack unit balls in space.
References. See also the Hales web page at http://www.math.lsa.umich.edu/~hales/.
[FT1] L. Fejes Tóth, Lagerungen in der Ebene auf der Kugel und im Raum, Die Grundlehren der Math. Wiss., Vol. 65, Springer-Verlag, Berlin, 1953, III.9, p. 84.
[FT2] L. Fejes Tóth, Regular Figures, International Series of Monographs on Pure and Applied Mathematics Vol. 48, Macmillan Co, NY, 1964, sect. 26, Cor., p. 183.
[FT3] L. Fejes Tóth, What the bees know and what they do not know, Bull. AMS 70 (1964), 468-481.
[M] Frank Morgan, The hexagonal honeycomb conjecture, Trans. AMS 351 (1999), 1753-1763.
[W] Hermann Weyl, Symmetry, Princeton Univ. Press, 1952, Princeton Sci. Lib. ed., 1989, p. 85.
OLD CHALLENGE (inspired by Wiley Miller). Player A writes three different integers, positive or negative, on three pieces of paper and reveals them one at a time. Player B selects one of the three when it is revealed, trying to pick the middle value. What are B's chances of winning? What are the best strategies? (What if B's goal is to pick the largest value?)
ANSWER. Of course B can win one-third of the time, just by picking his choice ahead of time at random. A can make sure that B can do no better than that by always starting with -1, 1, and then picking the third integer from {-2, 0, 2} at random. That way, the first two numbers revealed provide no information about which number is the middle one.
If B's goal is to pick the largest value, again B can win one-third of the time just by picking his choice ahead of time at random. Jean-Pierre Carmichael, , Joe Conrad, Joseph DeVincentis, and Glenn Iba observe that if A produces all six possible orderings at random, B can do better, can win half the time, by choosing the second number if it is bigger than the first and otherwise the third. (An article in the March American Mathematical Monthly, "Decision making: a golden rule," by Sardelis and Valahas, discusses such strategies.) But if B follows this strategy, then A can do much better by always making the first number the biggest!
According to Game Theory, A and B can finally settle down to a pair of strategies which neither will be able to improve. In this case A can still hold B to winning one-third of the time by always starting with say 0, followed by 1,2 or 1,-2 or -1,-2 each a third of the time. B can do no better than picking his choice head of time at random, with one-third probability of success.
For developing Game Theory John Nash won the 1994 Nobel Prize in Economics. The theory applies as well to strategies of business and war. We've recommended the recent Nash biography, "A Beautiful Mind," by Sylvia Nasar.
NEW CHALLENGE. Neville Barnard likes the equation 2 + 2 = 2 x 2, and asks for other similar equations, involving two or more numbers on each side of the equation.
Send answers, comments, and new questions by email to Frank.Morgan@williams.edu, to be eligible for Flatland and other book awards. Winning answers will appear in the next Math Chat. Math Chat appears on the first and third Thursdays of each month. Prof. Morgan's homepage is at www.williams.edu/Mathematics/fmorgan.
Copyright 1999, Frank Morgan.




