- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Symphonic Equations: A Mathematical Exploration of Music

Goldman, Caruthers, and Kung at the Carnegie Institution for Science
When St. Mary’s College of Maryland mathematics professor David Kung heard a public radio story about a presentation devoted to math and music, he took issue with the presentation’s title.
The seminar was called "Math and Music—Closer Than You Think," but, as Kung told a packed auditorium at the Carnegie Institution for Science on February 26, he already regarded the two disciplines as "epsilon apart."
Math-savvy members of the audience chuckled at this remark, but the MAA Distinguished Lecture "Symphonic Equations: A Mathematical Exploration of Music" also offered music enthusiasts plenty to engage with and mull over.
An amateur violinist himself, Kung had two of the "Closer Than You Think" musicians on stage with him: cellist Yvonne Caruthers and flutist Aaron Goldman, both members of the National Symphony Orchestra. The three of them presented a program in three movements, one focusing on each of overtones, resonance, and transformations. Musical interludes from a Vivaldi trio punctuated the evening.
The first movement bore the title "Symphony in a Single Note," an allusion to the complexity of the vibration that coaxes music from a string on a violin or the column of air inside a flute. (It’s not just a sine wave.) The discussion of overtones—which touched on differential equations and Newton’s laws of motion, summation notation, and boundary conditions—afforded Kung the opportunity to make two pet points about mathematics.
He asked the audience to use mathematical reasoning to determine whether covering the end of a tube would make it sound a higher, lower, or unchanged note when struck. He explained that, often, the goal of mathematics is to predict the future.
"I think we missed that in a lot of our math classes," Kung said. "It seems to me that when I was taking a lot of my math classes the goal wasn’t something so grand . . . the goal was more like to get through chapter four."
Kung also emphasized that the abstractness of mathematics gives it the power of broad application. Think about adding, he said. Although you first learn to add two piles of, say, apples, you soon discover that you can add other things.
"You can add fish, you can add cinnamon rolls, you can add spark plugs," Kung riffed. "Once you know the sort of abstract idea of addition, you can apply it in all of these different places."
The same math helpful in understanding musical overtones also describes the energy levels of an electron, Kung said.
In the second movement, titled "Bridges, Wineglasses, and the Bay of Fundy," Kung used the wooden boxes that form the bodies of stringed instruments as an entrée into the topic of resonance.
He corrected a common misconception—it was aeroelastic flutter that took down the Tacoma Narrows Bridge, not wind-speed resonance—and, with a demonstration of Tuvan throat singing, showed that his musical talents extend beyond his prowess on the violin.
The third and final movement, "Bach’s Mathematical Foresight," hearkened back to the earlier prediction theme. This time, though, it was Bach who anticipated the future of mathematics—through the use of transformations in the composition of his fugues and canons.
Although the mathematical study of transformations falls under the umbrella of group theory—pioneered by Gauss and Galois as recently as the early 1800s—Kung noted that "composers were using similar ideas long before."
Consider, for example, Canon 14 from Bach’s "Fourteen Canons on the First Eight Notes of the Goldberg Ground." It comprises a single line of music, along with a cryptic subtitle: "a canon in four parts with augmentation and diminution." Each of the second through fourth parts, it turns out, is derived from the written one via a combination of augmentation, transposition, and inversion.
Kung, Caruthers, and Goldman performed the canon, with Caruthers gamely assuming responsibility for the bottom two parts.
Before the final musical offering of the evening—the last movement of the Vivaldi trio—Kung reiterated the reciprocity that exists between math and music: "Math helps us understand music, and music helps us understand math," he said.
He also reminded the audience of a quote he’d introduced at the beginning of the third movement. Gottfried Leibniz said that "music is a secret exercise in arithmetic of the soul, unaware of its act of counting."
"I want you to listen for the 'arithmetic of the soul' that’s hidden in this music," Kung said. And brought his violin to his shoulder. —Katharine Merow
Watch "Symphonic Equations: Waves and Tubes," a miniexcursion into math and music
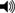 Listen to an interview with Kung and Ivars Peterson, MAA Director of Publications (mp3)
Listen to an interview with Kung and Ivars Peterson, MAA Director of Publications (mp3)

This MAA Distinguished Lecture was funded by the National Security Agency.




