- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Beauty for Truth's Sake: On the Re-Enchantment of Education

Publisher:
Brazos Press
Publication Date:
2010
Number of Pages:
156
Format:
Paperback
Price:
22.99
ISBN:
9781587432620
Category:
Monograph
[Reviewed by , on ]
Marcos B. Gouvêa
12/26/2011
I am not a mathematician, but I spent most of my formative years around them. But if I was never quite drawn into the fascination of my father and his colleagues, I was nonetheless sure of the charm of the thing. How else could you explain so many disparate people smiling at the elegance of one proof, or such pleasure in spotting the clever way out of a problem?
The author of this book is likewise not a mathematician. But he is eager to remind students of the humanities of a well-established tradition that respected and insisted on that charm. Caldecott wishes to inspire a recovery of the medieval and ancient perception of all that is, to move students to replace the vision of an inert universe with that of a cosmos: an order composed, balanced and articulated for worship. The author’s perspective is unabashedly Catholic but only incidentally apologetic: his main aim is to pique his readers’ interest in the possibility of a meaningful world. Granted so many examples of the elegant mathematical harmonies found in the stars, songs and spirits, the reader may really begin to wonder: what is behind all this? And can I join in?
To this end, Caldecott supplies a number of short discussions of how mathematical patterns are reflected in nature and culture. On the one hand, we hear of the orbit of planets, the harmonies of a scale, the appearance of φ in nature; on the other, about the role of such patterns in particularly fertile traditions of architecture and theology.
Ironically, the book’s greatest weakness lies in the author’s treatment of these crucial examples. To rehabilitate a Christian and/or neo-Pythagorean vision of world, Caldecott must commit to the view that mathematics is discovered, not invented. It is not the intention of this book to present an argument defending that claim, but the examples could stand to be a fair sight more charming. Particularly in the case of theology, one feels he wants us to feel more awe than he has earned.
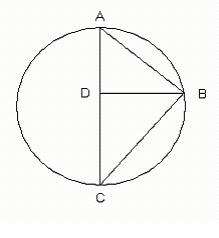 The most striking example may be his use of geometrical figures to illustrate certain characteristics of the Trinity (p.81ff.). Following Simone Weil, Caldecott begins with a circle and draws a right triangle ABC with the B lying on the circle’s perimeter and the diameter AC serving for the hypotenuse. In such a figure, the length of the line BD perpendicular to AC is the mean proportional of AD and DC.
The most striking example may be his use of geometrical figures to illustrate certain characteristics of the Trinity (p.81ff.). Following Simone Weil, Caldecott begins with a circle and draws a right triangle ABC with the B lying on the circle’s perimeter and the diameter AC serving for the hypotenuse. In such a figure, the length of the line BD perpendicular to AC is the mean proportional of AD and DC.
For Weil, this relationship seemed a powerful image of the incarnation, the relationship between circle and line being bridged as the Son of God bridges the gap between divinity and created humanity. Caldecott, however, sees a further meaning hidden here: “For if we multiply our Logos line by 7 we obtain a close approximation of the circumference of the circle (the exact multiplier is more like 7.025)” (p.86). Caldecott exegetes in the following way: seven is significant for being a symbol of perfection in the Bible, particularly in the creation narrative in Genesis; the remainder in the multiplier represents “the vital but infinitesimal human contribution [to salvation?], our free cooperation with grace” (p.87).
Protestant (and Augustinian!) objections aside, this meditation deflates the whole example. The power of Weil’s symbol lies in its accuracy; it is the elegance and necessity of the geometrical relationships that reminds us of dogma. In the author’s coda, however, the inexactness of the relation reduces us to an imposition of meaning. If it is not exactly seven, then to introduce the Biblical number seems forced; it is an introduction rather than a discovery of meaning. Even worse, the point about the remainder requires accuracy only of theology, not of geometry. Was not the point that they were mutually reinforcing?
This is perhaps the clearest instance of a significant problem with the book: in his excitement about the connections between mathematics and theology, Caldecott loses sight of the importance of mathematical and scientific proof as a means of persuasion. Barry Mazur once wrote that mathematicians who insist that math is discovered should “learn the trade, from prophets and lyrical poets, of how to communicate an experience that transcends the language available to describe it.” (See his article on Mathematical Platonism and its Opposites.) This gift Caldecott has in spades. What he lacks, however, is that training far more central to the mathematical trade, persuading his fellows with rigorous and even beautiful proofs. Without that particular charm, Caldecott will struggle to coax denizens of the mathematical universe to see the cosmos.
Marcos B. Gouvêa is the son of a mathematician and a candidate for a PhD in Classical Languages and Literatures at the University of Chicago. And yes, his Latin is better than his father’s.
The table of contents is not available.
- Log in to post comments




