Geometry Illuminated: An Illustrated Introduction to Euclidean and Hyperbolic Plane Geometry

An ‘illustrated’ book on plane geometry? Surely it couldn’t be otherwise. But ‘geometry illuminated’, and with no batteries included? What’s going on here?

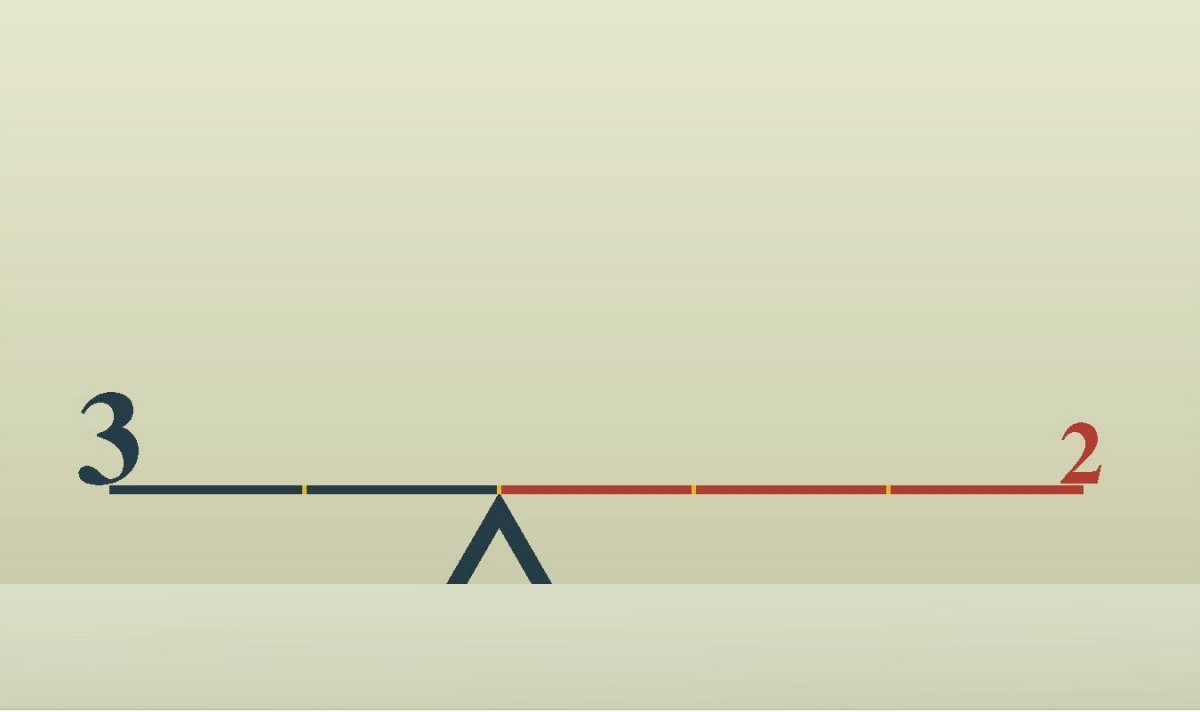
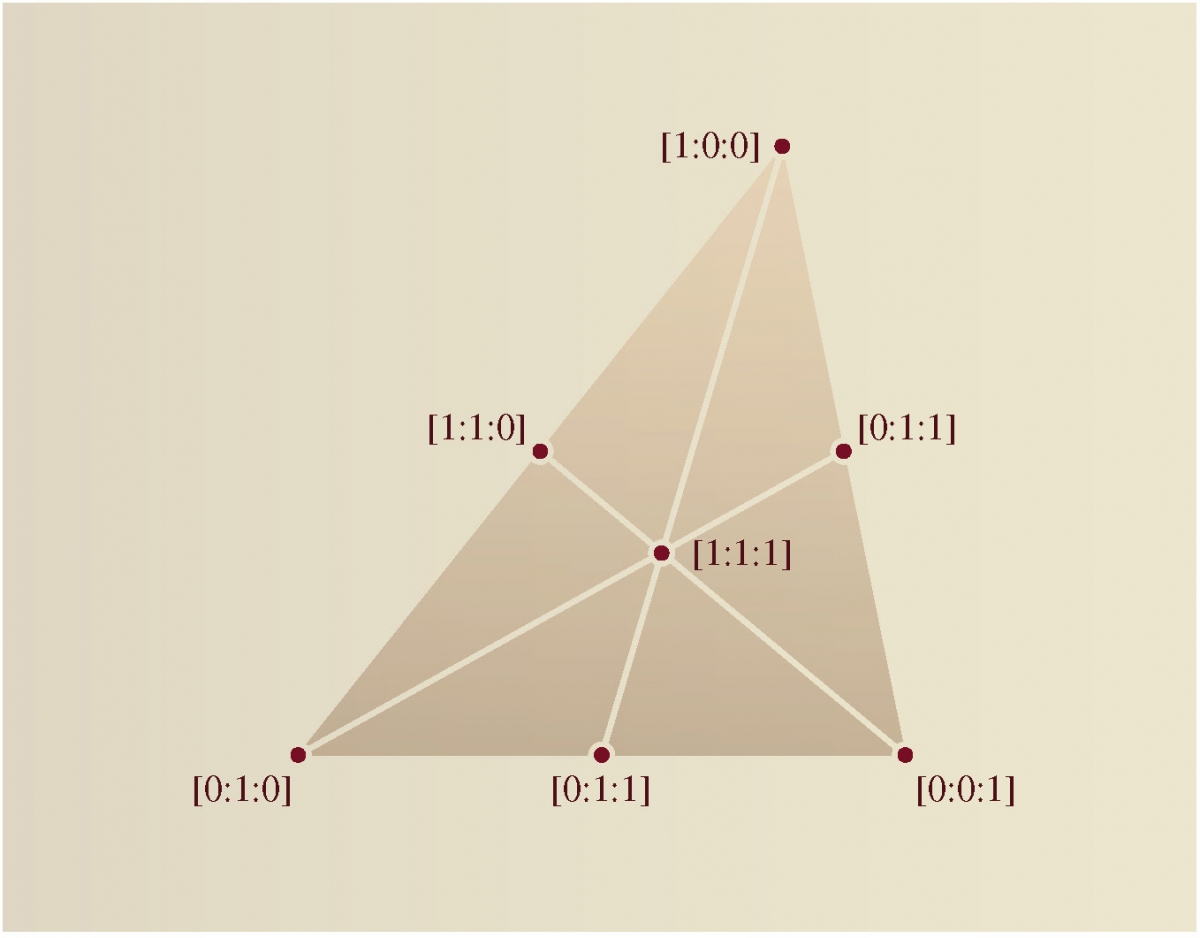Well, here is an example. In his introduction of barycentric coordinates, Matthew Harvey begins with the leverage principle of the simple seesaw, and then extends the analogy to a weighted mobile. He proceeds in stages to more conventional illustrations so that, within a few pages, the concept and techniques of barycentric and trilinear coordinates are firmly established and used to locate circumcentres and incentres of triangles.

(The color images in this review come from the ebook version and are used here with the publisher's permission; the printed version has grayscale images.)

This is typical of the whole book; the chapter on the pseudosphere contains a wealth of illustrations that would enhance any publication on differential geometry. Indeed, this book couldn’t be more fully provided with pictorial aids to understanding, and the abundance of artwork is why it is such a hefty tome (543pp).

Harvey offers a non-compartmentalized treatment of four main themes: Neutral Geometry, Euclidean Geometry, Euclidean Transformations and Hyperbolic Geometry. It is principally addressed to undergraduate math majors, who should have good understanding of the real number system, familiarity with basic linear algebra, complex numbers, differential equations and multivariable calculus. And yet, despite the extensive coverage of geometrical ideas provided here, there are several possible truncated routes through the book — each one forming the basis of a one-semester course (a semester on non-Euclidean geometry, for example).

The scene is set by a brief prologue on the importance of ‘Axioms and Models’ — as exemplified by the world’s smallest geometry (the Fano Plane). The spirit of David Hilbert pervades the subsequent introduction to neutral geometry, whilst Playfair’s axiom is the cornerstone upon which the ensuing edifice of Euclidean geometry is erected. Thus, Parts 1 and 2 occupy almost half the book, wherein the reader will have explored triangles in neutral geometry, the Saccheri-Legendre theorem and the scalene triangle theorem.

A major topic in Euclidean geometry is that of ‘concurrence’, and many lovely geometric properties emanate from this idea. For circles, there are the familiar notions of incentre, centroid, orthocentre and the surprising properties of the nine-point circle. Other pleasing Euclidean results include the Nagel point, the Euler line and the theorems of Ceva and Menelaus.

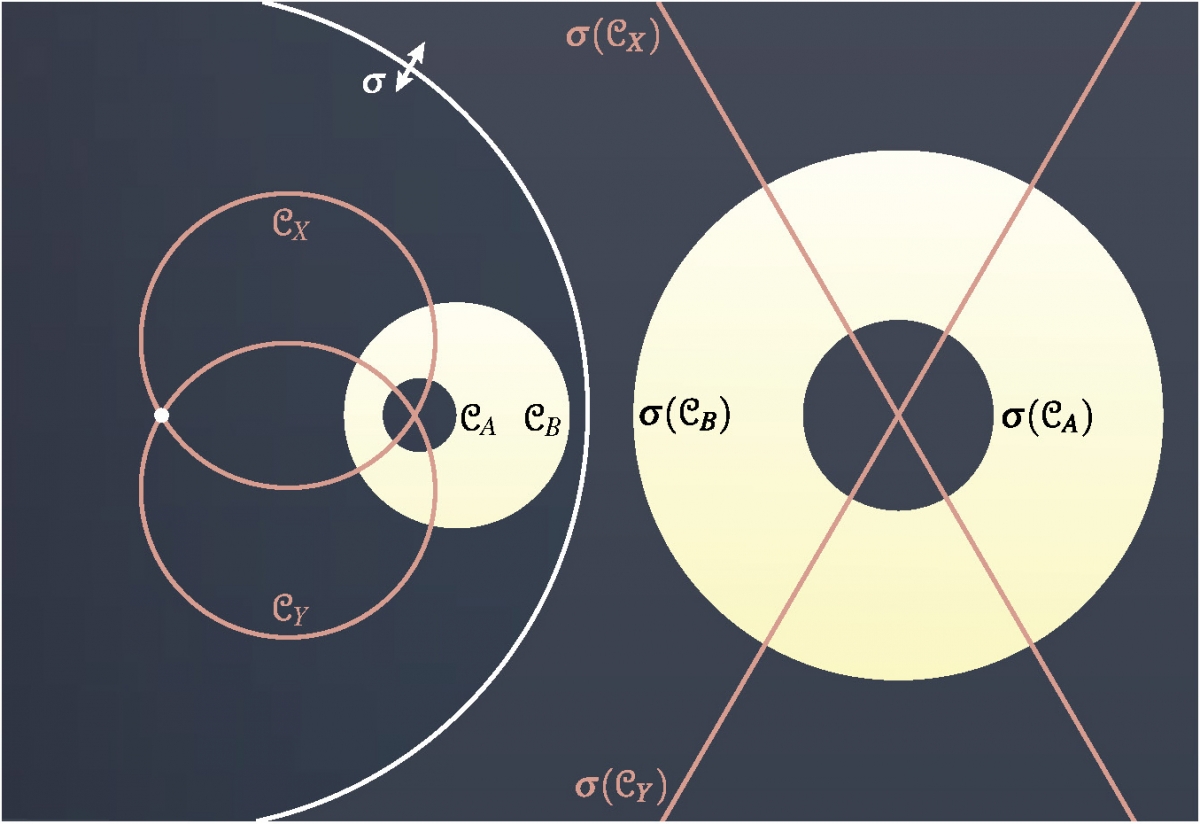A variety of such theorems are also established by use of the Euclidean transformations that are extensively discussed in Part 3. And, although this treatment doesn’t extend to affine transformations (or projective geometry), it concludes with a lengthy exposition on the use of inversion — which serves as a precursor for the ensuing coverage of hyperbolic geometry.

Non-Euclidean neutral geometry is initially viewed from the standpoint of the negation of Playfair’s axiom, and various models for hyperbolic geometry are introduced after that. For instance, multivariable calculus and linear algebra are brought to bear on the pseudosphere as a model of the hyperbolic geometry. And if it’s thought possible to introduce differential geometry (up to Gaussian curvature) within eight pages, then this is the book to do it. The motivation is, of course, the determination of geodesics on the pseudosphere. After that, the story is based on the Poincaré disc, which forms the context for hyperbolic isometries and hyperbolic trigonometry.

To my mind, this book stands out from the crowd partly because of the way in which its imaginatively devised illustrations are used to stage the introduction of basic concepts and to guide the reader through various steps in a proof. It’s not just a matter of pretty pictures, however, because Matthew Harvey’s written commentary is easy going and yet mathematically precise. He has written a truly lovely book, which is now top of my reading list as an introduction to geometry at this level.

Peter Ruane is retired from the field of mathematics education, which involved the training of primary and secondary school teachers. His postgraduate study included of algebraic topology and differential geometry, with applications to superconductivity.