Sequential Experiments with Primes

This book champions two wonderful ideas. The first is that mathematics can be performed through experimentation. The second is that undergraduates are quite qualified to conduct mathematical research. Neither statement is new. Sequential Experiments with Primes does a wonderful job weaving these themes together and illustrating them with numerous examples. Caragiu’s book is a lovely synthesis of both ideas illustrated with sequences based on prime numbers. The author’s goal is to show how mathematics professors can encourage undergraduate research and he has a hit with this book.

Experimental Mathematics

By way of background, an early discussion of experimental mathematics (see Experimental Mathematics) can be found in this groundbreaking book Mathematics by Experiment by Borwein and Bailey. More recently, for example, Sullivan, Townsend and Werzanski show how undergraduates conduct research in graph theory with “An Introduction to Lazy Cops and Robbers on Graphs” (The College Mathematics Journal, vol. 48, No. 5, November 2017).

One theme explored in the book is to encourage experimenters to play with sequences and maybe prove a conjecture. For example, many readers are undoubtedly familiar with the as yet unproven \( 3x + 1 \) Collatz conjecture. Choose a starting integer, say \( x_{0} \) and iterate as follows:\[x_n = \left\{ \begin{array}{l} \frac{1}{2} x_{n-1} \; \; \mbox{for } x_n \; \; \mbox{even} \\ \\ 3 x_{n-1} + 1 \; \; \mbox{for } x_n \; \; \mbox{odd} \end{array} \right.\] until the sequence takes the value \(1\). If you can prove the sequence always goes to \(1\) for any \(n\), then you will have proven the conjecture.

A theorem from the book

Caragiu gives his readers something new and exciting. I found the following theorem to be exquisite for its simplicity and experimental potential:

Theorem 3.1 If a, b are positive integers with \( a \mid b \), then every prime sequence \( \{ x_n \}_{n \geq 0} \) satisfying the recurrence \( x_{n} = P(a x_{n-1} + b) \) is ultimately periodic. (The function \( P( \cdot ) \) returns the greatest prime factor of the argument.)

Caragiu provides a readily understandable proof, but the real takeaway is just how simple the theorem is to understand and to play with it. Students can easily write an Octave function, plot results, and see for themselves if the function becomes periodic or not. This is experimental mathematics for number theory.

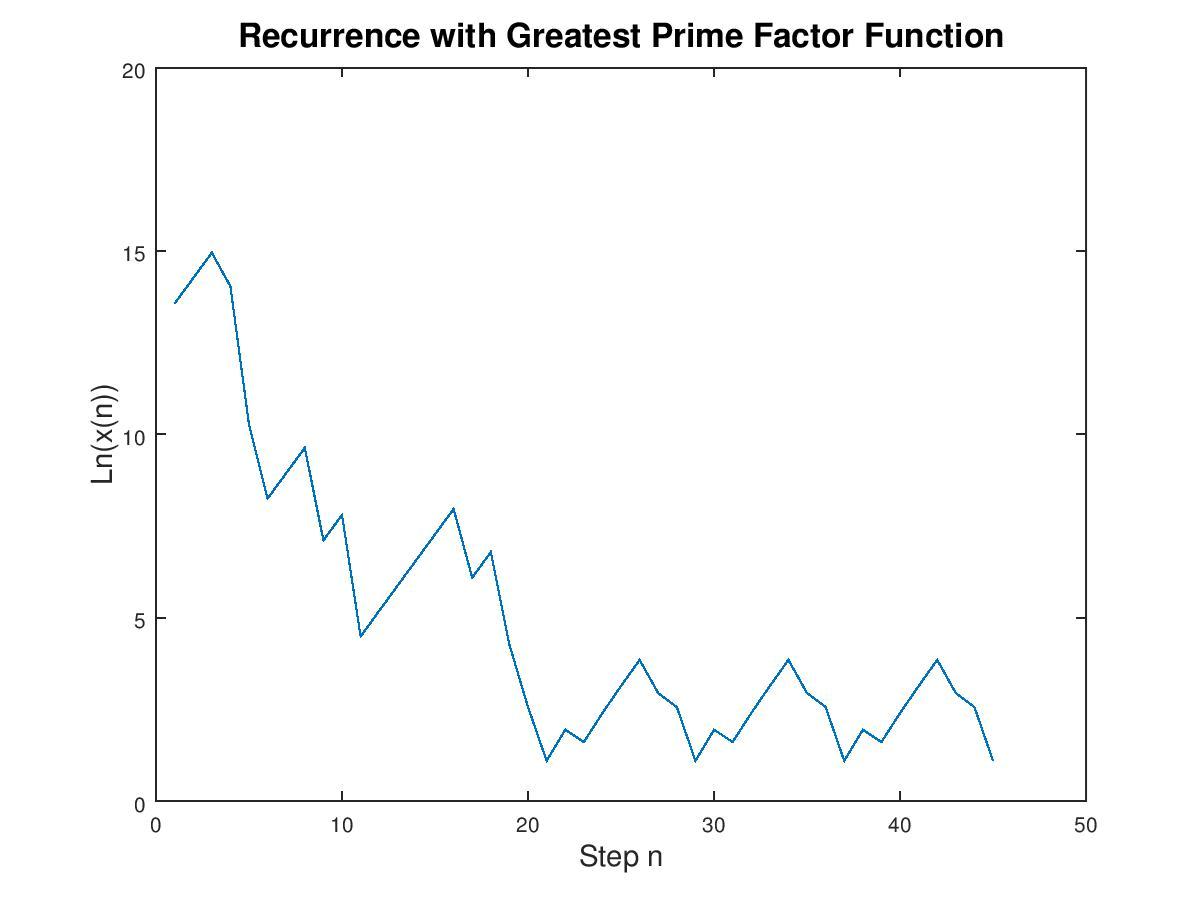
Figure 1: Example of a recurrence based on the greatest prime function.

I couldn’t resist a little play and reproduced a plot from the text, shown in Figure 1. This shows the largest number of iterations (that is, 19) to reach periodicity among all the primes less than 1,000,000 for the function: \( x_{n} = P(2x_{n-1} + 1 ) \; \; ; \; x_{0} = 779111 \) .

A project from the book

The book also offers what it calls “Computational Exploration Projects” as suggestions for student experimentations. CEP4, for example, asks the reader to experiment with a GPF-k-step-Fibonacci sequence having the recurrence relationship: \( x_{n} = P ( x_{n-1} +x_{n-2} + x_{n-3} + \cdots + x_{n-k} ) \)

Let’s take an example for \( k=3 \) and \( x_{0}=1, \; x_{-1} = 0 \; ; \; x_{-2} = 0 \) and we get the plot in Figure 2. The sequence is ultimately periodic with period 100. Note the peaks in the plot at sample indices 73, 173, 273, etc. I also tried this with the initial condition \( x_{0} = 47 ; \; x_{-1} = x_{-2} = 0 \) which produced a single-valued series. Can you see why that happened?

The author provides more experimental ideas such as multiple dimensional GPF sequences with recursions over matrices. I’ll leave the reader to explore the book for more details.

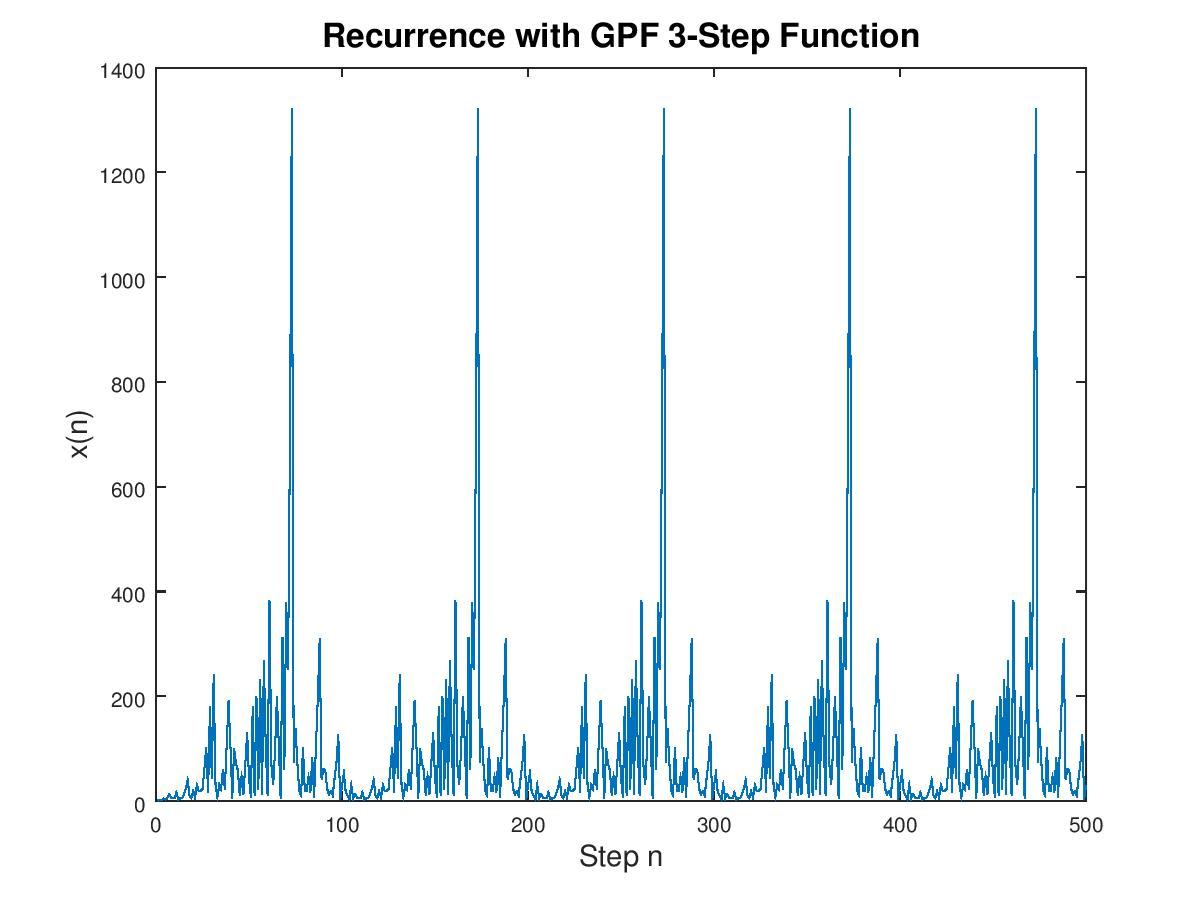
2: Example of a 3-term Fibonacci like sequence for the Greatest Prime Factor function.

By and large, this book offers you many ideas to explore and is an excellent foray into experimental mathematics. Caragiu calls out students by name for special mention; what a lovely way to recognize their work. The text mixes Maple and MATLAB scripts so readers can see implementations in two different languages.

A comment

The text is not without a few shortcomings. The editing could be improved, as I found a few typos. Plus, readers would benefit from figures with captions. While the author explains the figures with nearby text, a caption catches the eye and makes the figures more standalone.

In sum

Overall, this is an excellent book. If you are interested in experimental math and want to play, you’ll enjoy this book.

David S. Mazel is a practicing engineer in Washington, DC. He welcomes your thoughts and feedback. He can be reached at mazeld at gmail dot com.