- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Art of Insight in Science and Engineering

Publisher:
MIT Press
Publication Date:
2014
Number of Pages:
408
Format:
Paperback
Price:
30.00
ISBN:
9780262526548
Category:
Monograph
[Reviewed by , on ]
Tushar Das
08/4/2015
Sanjoy Mahajan is a trained physicist who teaches science and who is passionate about pedagogy. Mahajan’s infectious enthusiasm overflows onto every page of his new how-to-solve-it manual that is aimed at students and teachers of the physical sciences and engineering. The basic premise of his book is this: when attempting to understand the complexity of the world around us, one needs to cultivate insight rather than precision. The book boldly eschews rigorous methods, “for rigor easily becomes rigor mortis or paralysis by analysis,” and tries to comfort the reader early with “We’ll use as little mathematics as possible — algebra and geometry mostly, trigonometry sometimes, and calculus rarely — so that the mathematics promotes rather than hinders insight, understanding, and flexible problem solving.”
This genre of popular scientific writing, that may have had its first taste of commercial success with John Allen Paulos’s 1988 Innumeracy: Mathematical Illiteracy and Its Consequences, appears to have recently witnessed a revival of sorts, a recent example being Weinstein and Adam’s Guesstimation: Solving the World’s Problems on the Back of a Cocktail Napkin, whose success has since spawned a second volume.
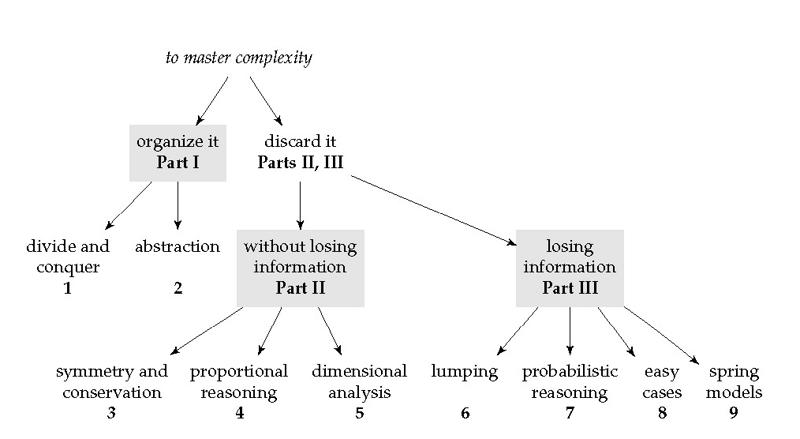
Mahajan has crafted his book based on his own teaching experiences and subsequent pedagogical revelations. A subtle shift in perspective led to a focus on teaching reasoning tools (one per chapter over nine chapters in total) and how to apply such tools to various topics, rather than the other way round starting with a list of topics from the physical sciences and then learning how to solve problems from each of those topics. The chapters are organized as shown in the following diagram taken from the preface:
This is the author’s second how-to-solve-it manual. His first book, Street-Fighting Mathematics, The Art of Educated Guessing and Opportunistic Problem Solving, was published in 2010. Mahajan is keen for readers to share suggestions and improvements and has made both his books available online under a Creative Commons Attribution Noncommercial Share Alike license. They may be found on the MIT press website. Though one could want every high-school STEM teacher to be encouraged to take a course or seminar out of one or both of Mahajan’s books while still in training, the wide range in both topics and sophistication makes the book very far from self-contained. A detailed instructor’s guide would probably help in increasing the book’s usage in classroom settings. That said, the problems are great fun. Instructors working in a college of science will gain a bag full of new ideas and examples to share with their classes. For example, Mahajan’s brief discussion of logarithmic scales (see Section 3.1.3) gave me more than a few ideas for when I next teach precalculus.
To give the potential reader some flavor of Mahajan’s style, I share a few of his discussions on one topic, the geometric mean, as they appear in various points along the book. The geometric mean first appears, somewhat mysteriously, when Mahajan is teaching us how to “talk to one’s gut” (in Section 1.6) as “the correct mean when combining quantities produced by our mental hardware”. He goes on to explain, more usefully, how it should be viewed as the midpoint between two endpoints on a logarithmic scale. Further down the road, we meet it on the beach: the approximate distance to the horizon, as seen from height \(h\) is \(\sqrt{Dh}\), where \(D\) is the diameter of the earth.
Later in Section 6.4.7, the “distance from the shore to the horizon“ idea is reapplied to solve an engineering problem: estimating the contact radius of a solid ball resting on the ground. The following appearance seemed curious enough to be worth quoting verbatim:
For me [Mahajan], its most surprising appearance was in the “Programming and Problem-Solving Seminar” course taught by Donald Knuth (who also created \(\TeX\), the typesetting system for this book). The course, taught as a series of two-week problems, helped first-year PhD students transition from undergraduate homework problems to PhD research problems. A homework problem requires perhaps 1 hour. A research problem requires, say, 1000 hours: roughly a year of work, allowing for other projects. (A few problems stapled together become a PhD.) In the course, each 2-week module required about 30 hours — approximately the geometric mean of the two end-points. The modules were just the right length to help us cross the bridge from homework to research.
As a last example I quote from one of the more challenging problems in the book (see p. 313): “The arithmetic and geometric means are easy cases of a higher-level abstraction: the power mean.” Mahajan goes on to define the \(k\)-th power mean of two positive numbers \(a\) and \(b\) as \[ M_k(a,b) \equiv \left(\frac{a^k + b^k}{2}\right)^{\frac1k} , \] and after asking the reader to figure out what \(k\) should be to get the arithmetic mean, the root mean square, and harmonic mean of \(a\) and \(b\), he ends with the following teaser: “(Surprising!) What is $k$ for the geometric mean?”
For fun I surveyed a number of my colleagues (both pure and applied mathematicians, and mathematics educators) to ask what a geometric mean really meant, and where it might be located in their own mathematical corpus. Almost none of their answers aligned with the rich variety of ideas presented by Mahajan!
There were a number of places where the mathematics and physics being discussed was sufficiently sophisticated that readers must be prepared for steep learning curves. Sophistication aside, various parts of the book will make a mathematician cringe. For example, consider the following discussion from the beginning of Section 6.3.4:
Acceleration is the derivative of velocity: \(a=dv/dt\). Using the definition of derivative, \[ \frac{dv}{dt} = \frac{\text{infinitesimal change in }v}{\text{(infinitesimal) time required to make this change in }v}.\] Infinitesimal changes and times are difficult to picture, so an analysis based on calculus often does not help us see why a result is true.
A lumping approximation, by discarding complexity, can give this insight. A way to remember the lumping approximation, first use \(6 = 6\) to cancel the \(6\)s in \(16/64\): \[ \frac{1\!\!\!\not{6}}{\not{6}4}=\frac{1}{4}.\] The result is exact! Although this particular cancellation is dubious, it suggests the analogous lumping approximation \(d=d\). The resulting cancellation turns derivatives into algebra: \[ \frac{\not{\!d}v}{\not{d}t} \sim \frac{v}{t}.\]
Despite misgivings, Mahajan has written an inspiring though racy (some might even call it dangerous) book. He teaches you to jump in and “gutstimate” via simple, easy-to-apply reasoning tools, and so overcome your worst fears when overwhelmed by the complexity of the problem before you. It will pay great dividends to a highly-motivated and obsessively curious reader.
Tushar Das is an Assistant Professor of Mathematics at the University of Wisconsin–La Crosse.
|
Part I |
Organizing complexity 1 Divide and conquer 2 Abstraction |
|
Part II |
Discarding complexity without losing information 3 Symmetry and conservation 4 Proportional reasoning 5 Dimensions |
|
Part III |
Discarding complexity with loss of information 6 Lumping 7 Probabilistic reasoning |
|
Index Bibliography |
- Log in to post comments




