Who's #1? — The Science of Rating and Ranking

As most anyone with even a passing interest in sports is aware, sports rankings are now a virtual obsession with the media. Since rankings are subject to mathematical analysis, many mathematicians (and others) have constructed ranking systems of widely varying credibility. From the widely disparaged BCS ratings in college football to the latest Vegas line, ratings and their associated rankings are everywhere. Besides the big business of college sports, Netflix also uses a ratings system to rate its films. They awarded a $1 million prize to a team who improved their ratings system by 10%. And, of course, there is the Google page ranking system, the subject of an earlier book, Google’s PageRank and Beyond: The Science of Search Engine Rankings, by the same authors. Who’s #1 provides a fascinating tour through the world of rankings and is highly recommended.

To be clear before we delve into the details: a rating system assigns a number to each of a set of teams. Those same teams can then be ranked (1^st, 2^nd, …) based on their numerical rating. The BSC system assigns a decimal between 0 and 1 to each team in its rating universe. Ranking is then computed by ranking the team with the highest BSC rating as #1 and then moving down the line. Ranking can be done by a voting system (also part of the BCS ranking system) but such voting schemes are subject to Arrow’s results and thus never certain to produce results which satisfy even minimal conditions such a voting scheme ought to satisfy (pages 3–4).

Who’s # 1 provides a generous sampling of the various ways to construct a rating system as well as an analysis of the strengths and weaknesses of each of them. There are several examples used throughout. Here’s one of them: how would you rate these 5 football teams based on their performance against each other?

(Baffled by the initials? UNC = University of North Carolina, UVA = University of Virginia, and VT = Virginia Tech.)

There are two obvious ways to rate the teams: win-loss record and total point differential. These yield the following ratings and associated rankings:

While the two ratings agree on 3 of the 5 teams, the point differential reverses the ranking for UVA and UNC. Even though UNC won 2 games and UVA won only 1, UVA lost by a smaller overall margin. However, a closer analysis reveals this was due mostly to the fact that UVA beat Duke by 31 points while UNC beat Duke by only 3. Perhaps UVA ran up the score against the hapless Blue Devils and we shouldn’t give them so much credit for that? The issue of point differential and the presumed evil of teams running up the score against weaker opponents surfaces again and again as various rating schemes are considered.

Just how different are these two rankings? Chapter 16 investigates just that topic — the quantitative measure of concordance/discordance among two ranked lists. The simplest (assuming both lists contain the same teams/items) is the Kendall Tau (page 204):

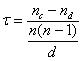
Here n_c represents the number of times two teams are ranked the same in each list, while n_d represents the number of times the rankings differ (in either direction). The denominator represents the total number of such comparisons and hence –1 ≤ τ ≤ 1, with 1 representing perfect agreement and –1 representing complete disagreement. In our example, τ = .8. Needless to say, this is not all that can be said about such comparisons — consult chapter 16 for the details.

Each chapter presents one or more seemingly plausible ratings systems along with a bit of history concerning their creation. Here are two examples.

Massey Rating System

Created in 1997 by Kenneth Massey as part of his honors thesis at Bluefield College, this rating is one of those used in the BCS ratings scheme. In its simple form, the Massey systems uses least squares analysis to find a set of ratings r_i with the property that the difference in ratings predicts the margin of victory/defeat when team i plays team j (r_i – r_j = y_k). We thus start with a matrix equation of the from Xr = y, where the margins of victory are known (for games already played) and we are seeking to find a least squares solution for vector r. This is overdetermined and inconsistent so Massey solves the normal equation X^TXr = X^Ty. Adding the constraint that the sum of all ranks must be 0 yields the following Massey Rating for our intrepid ACC football rivals:

Massey added an additional wrinkle by creating offensive and defensive rankings for each team; a system which allows Duke to crawl out of the cellar in one category by placing 4^th in Offensive Ranking. For more on Massey consult Who’s #1? or google “Massey.” The remainder of the chapter outlines the other components of the BSC formula including the Notre Dame rule. See page18 for details.

Chess and the NFL: The Elo Rating System

From college football we move to chess — where rankings carry less monetary but significantly greater political significance. Those of us who were alive when Bobby Fisher was at his peak recall that a drop in his ranking was considered tantamount to our losing the cold war. The method discussed was created by Arpad Elo, a physics professor at Marquette University. His notion was to treat a player’s performance as a normally distributed random variable X whose mean µ changes only very slowly after a player’s game is established. As the system was implemented it was discovered that performance is not generally normally distributed. The current system assumes that expected scoring difference between two players is a logistic function of their ratings.

Langville and Meyer complete the chapter on Elo ratings with an analysis of the 2009–2010 National Football League season. With full season data, the Elo ratings correctly predict (hindsight accuracy) 75.3% of all games. Computing the Elo ratings as the season progressed yields a foresight accuracy of 62.2%. That’s pretty good, but winning at Vegas requires not just picking the winner, but the margin of victory — for that analysis proceed to chapter 9!

I would recommend this book for any college library. It’s a great source of projects for students at all levels. Beginning students could try some of the schemes on their local athletic conference while advanced students could attempt to add to the collection of ratings schemes and dream of saving (or destroying) the BCS.

Richard Wilders is Marie and Bernice Gantzert Professor in the Liberal Arts and Sciences and Professor of Mathematics at North Central College. His primary areas of interest are the history and philosophy of mathematics and of science. He has been a member of the Illinois Section of the Mathematical Association of America for 30 years and is a recipient of its Distinguished Service Award. His email address is [email protected].