American Mathematical Monthly - April 2017

The April issue of the Monthly offers many springtime treats: connections between error-correcting codes and sporadic Mathieu groups, convergent power series methods for solving differential equations modeling tides, angles in integer-side-length “grade school” triangles, Lexell’s theorem for spherical triangles, and Ulam’s problem whether all subsets of the plane can be obtained from the σ-algebra of generalized rectangles.

In the Notes section, you can encounter a superpowered prime generator, the greatest common divisor of binomial coefficients, a combinatorial proof of a theorem of Frobenius about number of m-torsion elements in a group, how to determine convergence of series whose terms are defined recursively, and a simple and a negative answer to Golomb’s conjecture on prime gaps: that there is no increasing sequence {a_k} of positive integers and positive constant B such that {a_k + n} contains at most B primes for every integer n.

Besides tantalizing problems for your consideration, Marion Cohen reviews Mom the Chemistry Professor: Personal Accounts and Advice from Chemistry Professors Who are Mothers, a book that spotlights the dilemmas and delights that face women scientists raising children.

Happy reading!

  — Susan Jane Colley, Editor

JOURNAL SUBSCRIBERS AND MAA MEMBERS:

To read the full articles, please log in to the member portal by clicking on 'Login' in the upper right corner. Once logged in, click on 'My Profile' in the upper right corner.

Table of Contents

Build a Sporadic Group in Your Basement

p. 291.

Paul E. Becker, Martin Derka, Sheridan Houghten and Jennifer Ulrich

All simple finite groups are classified as members of specific families. With one exception, these families are infinite collections of groups sharing similar structures. The exceptional family of sporadic groups contains exactly twenty-six members. The five Mathieu groups are the most accessible of these sporadic cases. In this article, we explore connections between Mathieu groups and error-correcting communication codes. These connections permit simple, visual representations of the three largest Mathieu groups: M₂₄, M₂₃, and M₂₂. Along the way, we provide a brief, nontechnical introduction to the field of coding theory.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.291

Convergent Power Series for Boundary Value Problems and Eigenproblems with Application to Atmospheric and Oceanic Tides

p. 306.

John P. Boyd and Houjun Wang

It is usually impossible to apply power series to solve boundary value and eigenvalue problems because the radius of convergence does not extend to the boundaries. Hough functions, which solve a second order eigenproblem, are always entire functions or can be computed wholly in terms of entire functions. The eigenvalues ε are approximated by the zeros of the highest computed power series coefficient, which is always a polynomial in ε. The rate of convergence with series truncation N is proportional to exp(−μN) for some positive constant μ. A brief table contains the entire Maple code for the algorithm. The scheme can also be extended to eigenproblems on an unbounded domain as here illustrated by the quantum harmonic oscillator and quartic oscillator. Computer algebra is very useful; the power series method can also be implemented in a stable, purely numerical fashion by applying trigonometric interpolation on a disk in the complex x-plane and Chebyshev interpolation on a real interval in ε. Power series are briefly compared with Chebyshev, Fourier, and spherical harmonic spectral methods, which are mostly superior. The success of power series raises an interesting history-of-science issue: Why was there so little progress in solving Laplace’s tidal equations in the nineteenth century?

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.306

More Grade School Triangles

p. 324.

Arno Berger

Planar triangles with each side having a positive integer length are among the simplest geometrical objects imaginable. What can be said about the angles of such triangles? In particular, are these angles rational or at least algebraic numbers when measured in degrees? This article demonstrates that the answer in general is negative, except for three distinguished families of triangles. One family is well known since antiquity: With the largest angle equal to 90 degrees, it simply is the family of Pythagorean right triangles. Though not nearly as well-known, the other two families also deserve to be part of every geometry teacher’s toolkit.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.324

On Lexell’s Theorem

p. 337.

Hiroshi Maehara and Horst Martini

Lexell’s theorem states that two spherical triangles ABC and ABD have the same area if C and D lie on the same circular arc with endpoints A* and B*, which are the antipodal points of A and B, respectively. We present an elementary treatment for the case that the circular arc is a semicircle. In addition, a new proof of Lexell’s theorem is presented, without using Girard’s theorem. Finally, we give an improved version of Lexell’s theorem in terms of the chord-tangent angle.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.337

A Little Ado about Rectangles

p. 345.

Antonio Avilés and Grzegorz Plebanek

We discuss a problem of Ulam: whether every subset of the plane can be obtained by making countably many set operations with generalized rectangles.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.345

Notes

A Superpowered Euclidean Prime Generator

p. 351.

Trevor D. Wooley

A variant of Euclid’s prime generator is discussed with some of its brethren.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.351

On the Greatest Common Divisor of Binomial Coefficients

p. 353.

Carl McTague

Every binomial coefficient aficionado knows that the greatest common divisor of the binomial coefficients 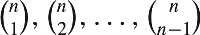 equals p if n = pⁱ for some i > 0 and equals 1 otherwise. It is less well known that the greatest common divisor of the binomial coefficients  equals (a certain power of 2 times) the product of all odd primes p such that 2n = pⁱ + p^j for some 0 ≤ i ≤ j. This note gives a concise proof of a tidy generalization of these facts.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.353

A Counting Proof of a Theorem of Frobenius

p. 357.

David E. Speyer

Frobenius showed that, if m divides the order of a finite group, then the number of m-torsion elements in that group is divisible by m. We provide a quick combinatorial proof.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.357

Convergence for Series With Terms Defined by a Recurrence Relation

p. 360.

Evelyn R. Easdale, Jolene E. Fleming and Bogdan D. Suceavă

We investigate whether a series    with terms defined recursively by the relation x_n+1 = f (x_n), for all n ≥ 1, converges or diverges. For the examples studied, the ratio test is inconclusive. We provide a theorem to decide whether such series are either convergent or divergent under some natural analytic conditions.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.360

Golomb’s Conjecture on Prime Gaps

p. 365.

Christian Elsholtz

Question 10208b (1992) of THIS MONTHLY asked: Does there exist an increasing sequence {a_k} of positive integers and a constant B > 0 having the property that {a_k + n} contains no more than B primes for every integer n? A positive answer to this question became known as Golomb’s conjecture. In this note, we give a negative answer, making use of recent progress in prime number theory.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.365

Problems and Solutions

p. 369.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.369

Book Review

p. 379.

Mom the Chemistry Professor: Personal Accounts and Advice from Chemistry Professors Who Are Mothers edited by R. Cole, C. Marzabadi, G.Webster, and K.Woznach

Reviewed by Marion Cohen

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.379

MathBits

100 Years Ago This Month in The American Mathematical Monthly

p. 323.

A Telescoping Proof of the AM–GM Inequality

p. 356.

Mehtaab S. Sawhney

DOI: http://dx.doi.org/10.4169/amer.math.monthly.124.4.356