- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
American Mathematical Monthly -August/September 2009
![]()
August/September 2009
Ramanujan's Series for 1/π : A Survey
By: Nayandeep Deka Baruah, Bruce C. Berndt, and Heng Huat Chan
nayan@tezu.ernet.in, berndt@math.uiuc.edu, matchh@nus.edu.sg
In his famous paper "Modular equations and approximations to π,'' Ramanujan stated 17 infinite series representations for 1/π, which were not entirely proved until 1987. This paper provides a survey of Ramanujan's series for 1/π, further series for 1/π, their roles in calculating the digits of π, and the connections of these series with other investigations in number theory. We will discuss, in particular, the contributions of S. Chowla, R. William Gosper, Jr., Jonathan and Peter Borwein, David and Gregory Chudnovsky, Jesús Guillera, Gabriella Montez (the precocious student in the movie "High School Musical''), and the authors. Ramanujan's ideas, which depend on Eisenstein series, will be examined in detail with one example.
Almost All Integer Matrices Have No Integer Eigenvalues
By: Greg Martin and Erick B. Wong
gerg@math.ubc.ca, erick@math.ubc.ca
We examine the probability that a square matrix with integer entries is singular (hence has 0 as an eigenvalue) and the probability that a square matrix with integer entries has at least one integer eigenvalue. Both of these probabilities depend upon a bound for the absolute value of the size of the integer entries; our quantitative results show that both probabilities tend to 0 as the bound increases. These results answer a question, posed by Hetzel, Liew, and Morrison in a recent issue of this Monthly, on the diagonalizability of randomly chosen matrices with integer entries.
New Insight into Cyclodial Areas
By: Tom M. Apostol and Mamikon A. Mnatsakanian
apostol@caltech.edu, mamikon@caltech.edu
A point on the boundary of a circular disk that rolls once along a straight line traces a cycloid. The cycloid divides its circumscribing rectangle into a cycloidal arch below the curve and a cycloidal cap above it. The area of the arch is three times that of the disk, and the area of the cap is equal to that of the disk. The paper provides deeper insight into this well-known property by showing (without integration) that the ratio 3:1 holds at every stage of rotation. Each cycloidal sector swept by a normal segment from the point of contact of the disk to the cycloid has area three times that of the overlapping circular segment cut from the rolling disk. This surprising result is extended to epicycloids (and hypocycloids), obtained by rolling a disk of radius r externally (or internally) around a fixed circle of radius R. The factor 3 is replaced by (3 + 2r/R) for the epicycloid, and by (3 – 2r/R) for the hypocycloid. This leads to several interesting consequences. For example, for any cycloid, epicycloid, or hypocycloid, the area of one full arch exceeds that of one full cap by twice the area of the rolling disk. Other applications yield (again without integration) compact geometrically revealing formulas for areas of cycloidal radial and ordinate sets.
Branched Polymers
By: Richard Kenyon and Peter Winkler
A branched polymer is a connected configuration of non-overlapping unit balls in space. Building on and from the work of David Brydges and John Imbrie, this article presents an elementary calculation of the volume of the space of branched polymers of order n in the plane and in 3-space. Our development reveals some more general identities, and allows exact random sampling. In particular we show that a random 3-dimensional branched polymer of order n has diameter of order 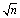 . Along the way, we give the first elementary proof of Rayleigh's notorious "random flight" theorem, which says that the probability that an n-step unit-vector random walk in the plane ends within distance one of its starting point is 1/(n+1).
. Along the way, we give the first elementary proof of Rayleigh's notorious "random flight" theorem, which says that the probability that an n-step unit-vector random walk in the plane ends within distance one of its starting point is 1/(n+1).
Notes
On a Theorem of Abel
By: Shui-Hung Hou
mahoush@inet.polyu.edu.hk
In this note, we provide an elementary proof of a theorem of Abel, which states that if P(x) and Q(x) are two polynomials such that  , Q(x) has no multiple roots, and
, Q(x) has no multiple roots, and  , then
, then 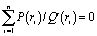 , where r1,...,rn are the n distinct roots of Q(x).
, where r1,...,rn are the n distinct roots of Q(x).
Ramanujan Primes and Bertrand's Postulate
By: Jonathan Sondow
jsondow@alumni.princeton.edu
The nth Ramanujan prime is the smallest natural number Rn such that for all x ≥ Rn the interval (x/2,x] contains at least n primes. Bertrand's postulate is R1 = 2. Ramanujan proved that Rn exists and gave the first five values as 2, 11, 17, 29, 41. In this note we provide upper and lower bounds for Rn, and show that it is asymptotic to the 2nth prime. We also estimate the length of strings of consecutive Ramanujan primes among all primes, explain why there are more twin Ramanujan primes than expected, and make three conjectures.
Light Subsets of N with Dense Quotient Sets
By: Shawn Hedman and David Rose
shedman@flsouthern.edu, drose@flsouthern.edu
If a set S of natural numbers has natural density greater than zero, then the set of quotients of elements of S is dense in the positive reals. We show that the converse of this fails in a strong way. If S has natural density zero, then it is said to be light. We generalize this notion and show that there exist arbitrarily light sets of natural numbers having dense quotient sets.
The Least Prime in Certain Arithmetic Progressions
By: Juan Sabia and Susana Tesauri
jsabia@dm.uba.ar, stesauri@dm.uba.ar
In this note we give an upper bound for the least prime in certain arithmetic progressions. Although Linnik’s theorem gives an asymptotically more precise bound, the proof here is completely elementary and is based on an observation already made by Legendre in 1830.
A Simple Continuous Bijection from Natural Sequences to Dyadic Sequences
By: Oliver Deiser
deiser@math.fu-berlin.de
We construct a simple continuous bijection from the space of all infinite sequences of natural numbers to the space of all infinite dyadic sequences.
Reviews
Basic Real Analysis and Advanced Real Analysis
By: Anthony W. Knapp
Reviewed by: Neil Falkner





