American Mathematical Monthly - February 2015

Thaw out from that harsh winter freeze with the February Monthly. In our lead articles, Yves Nievergelt explains to us the ins and outs of Backward Analysis in “Backward Analysis Explained with Monthly Payments,” and Chris O’Neill and Roberto Pelayo offer us a way to measure the degree of primeness of an element in “How Do You Measure Primality?” Gerald Folland reviews “Hidden Harmony—Geometric Fantasies: The Rise of Complex Function Theory” by Umberto Bottazzini and Jeremy Gray.” The Problem Section will help you warm up by the fire. Help us celebrate Pi Day in March with a special paper covering the history of Pi in the Monthly by Jon Borwein and Scott Chapman. See you then! - Scott T. Chapman, Editor

JOURNAL SUBSCRIBERS AND MAA MEMBERS:

To read the full articles, please log in to the member portal by clicking on 'Login' in the upper right corner. Once logged in, click on 'My Profile' in the upper right corner.

Backward Analysis Explained with Monthly Payments

Yves Nievergelt

Using only algebra, this exposition presents the concept of backward analysis. Numerical examples from finance demonstrate how backward analysis guarantees that the computed value of a polynomial of degree exceeding thirty-one million is accurate to all but the penultimate digit, despite a hundred million intermediate rounding errors. Methods from celestial mechanics then provide initial estimates for the solution of financial polynomial equations. The same analysis applies to the computation of elementary functions from calculus and special functions from differential equations.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.122.02.91

How Do You Measure Primality?

Christopher O’Neill and Roberto Pelayo

In commutative monoids, the ω-value measures how far an element is from being prime. This invariant, which is important in understanding the factorization theory of monoids, has been the focus of much recent study. This paper provides detailed examples and an overview of known results on ω-primality, including several recent and surprising contributions in the setting of numerical monoids. As many questions related to ω-primality remain, we provide a list of open problems accessible to advanced undergraduate students and beginning graduate students.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.122.02.121

A New Proof for a Sharp van der Corput’s Lemma

Carlos A. Catalá de la Torre

We give a simple proof of a sharper bound in a van der Corput’s lemma found by K. Rogers in 2005. Continuity and a simple system of ODEs are used for proving the sharp bound. This lemma is of special interest in analytic number theory as well as the theory of oscillatory integrals, which appear frequently throughout mathematics.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.122.02.138

Geometry of the Cardioid

Arseniy V. Akopyan

In this article, we discuss the cardiod. We give purely geometric proofs of its well-known properties.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.122.02.144

Notes

Elementary Prime Identities

G. Molinari

We prove an identity involving prime numbers, which gives new elementary proofs of two well-known prime properties. Furthermore, the identity and its corollaries may contribute to a better understanding of the distribution of the primes.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.122.02.151

On Elementary Bounds for

Joachim Gräter and Karl-Joachim Wirths

By means of elementary arguments, we derive lower and upper bounds for the infinite series

DOI: http://dx.doi.org/10.4169/amer.math.monthly.122.02.155

An Easy Generalization of Euler’s Theorem on the Series of Prime Reciprocals

Paul Pollack

It is well known that Euclid’s argument can be adapted to prove the infinitude of primes of the form 4k − 1. We describe a simple proof that the sum of the reciprocals of all such primes diverges. More generally, if q is a positive integer and H is a proper subgroup of the units group (Z/qZ) ×, we show that .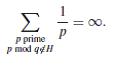

DOI: http://dx.doi.org/10.4169/amer.math.monthly.122.02.159

A Comprehensive Pythagorean Theorem for all Dimensions

Daniel Drucker

We use a 200-year-old theorem on determinants to prove a very general version of the Pythagorean theorem. It relates the square of the n-dimensional volume of an n-parallelotope in Rm to the sum of the squares of the n-dimensional volumes of the orthogonal projections of the parallelotope onto the k-dimensional coordinate subspaces of Rm.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.122.02.164

Two Elementary Properties of Entire Functions and Their Applications

Bao Qin Li

We give two elementary properties for entire functions. The first is a direct consequence of Cauchy’s theorem, which implies both Liouville’s theorem and the Fundamental Theorem of Algebra. The second is an analytic version of the Fundamental Theorem of Algebra for entire functions, which also gives a characterization of polynomials with a prescribed degree.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.122.02.169