- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
An Investigation of Historical Geometric Constructions - Using the Quadratrix to Trisect an Angle
Once the quadratrix has been formed, move point E anywhere along arc BED. Using Hippias’ method, we will find an angle one-third the measure of angle DAE. Move points C' and E such that point F is the intersection of the quadratrix and AE (see Figure 10).
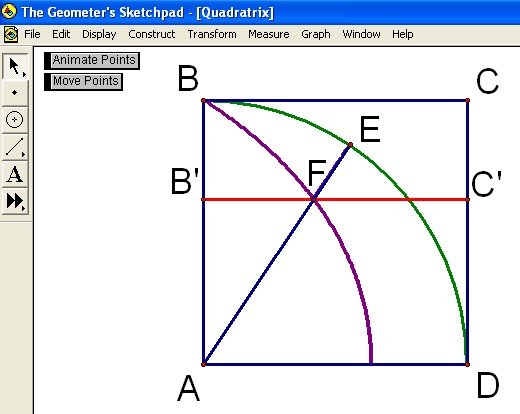
Figure 10: Using the Quadratrix To Trisect Angle DAE
Construct a perpendicular line to AD through the point F. Construct the intersection point of this perpendicular line and segment AD and label it H. Next construct segment FH and hide line FH. The trisection of an angle has now been reduced to trisecting the line segment FH. Formally construct a point (K) along FH such that HK is one-third the length of FH. Click here to see the animation of this construction.
Construct a parallel line to AD through point K. Identify the intersection of the parallel line with the quadratrix, and name this point J. Construct ray AJ. The measure of angle DAJ is one-third the measure of angle DAE (see Figure 11).
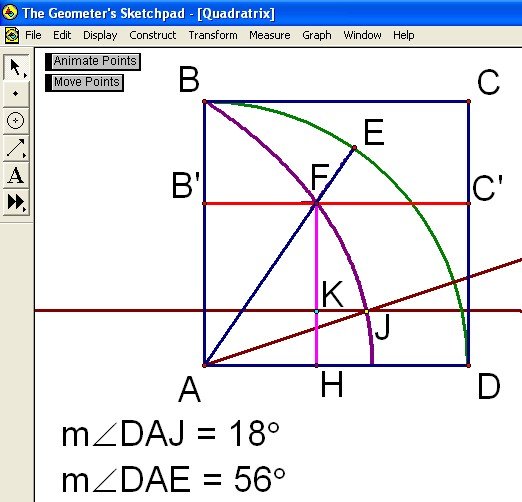
Figure 11: Using the Quadratrix to Trisect Angle DAE
As one can see, the quadratrix can be used to easily reduce the problem of trisecting an angle to that of trisecting a line segment; furthermore Hippias generalized this method to subdivide any given angle into any number of equal subangles.
Although many scholars attempted to trisect an angle, the more popular construction of the three famous geometric construction problems was to find a square with the same area as a given circle. Hippocrates of Chios made major contributions toward mathematics while trying to solve this problem.
Suzanne Harper and Shannon Driskell, "An Investigation of Historical Geometric Constructions - Using the Quadratrix to Trisect an Angle," Convergence (August 2010)




