- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Can You Really Derive Conic Formulae from a Cone? - Deriving the Symptom of the Acute-angled Cone
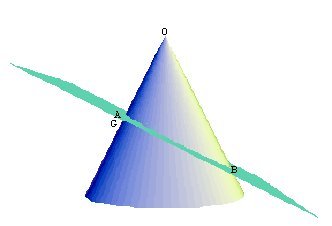 Consider the acute-angled cone with vertex O and a plane intersecting a generating line OG at a right angle at point A. The plane intersects the cone in the oxytome with diameter AB.
Consider the acute-angled cone with vertex O and a plane intersecting a generating line OG at a right angle at point A. The plane intersects the cone in the oxytome with diameter AB.
A dynamic view of this construction will be helpful in what follows.
[In order to open the dynamic view in a new window to allow you to show the text and the derivation side-by-side, right click or Ctrl-click on the link.]
 |
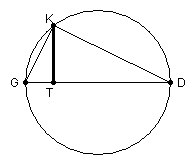 |
Consider an arbitrary ordinate (i.e. y value) TK constructed on the axis at T. We wish to determine the relationship between TK and AT, that is, the symptom of the conic. The ordinate TK is located in a horizontal plane that cuts the cone in the circle with diameter DG. In this horizontal plane construct the segments GK and DK, which results in a right triangle inscribed in a semicircle. (The triangle is right by Elements, Book III, Proposition 20). We also know that triangles GTK and KTD are similar (by Book VI, Prop. 8) and this implies
|
|
|
|
|
(1) |
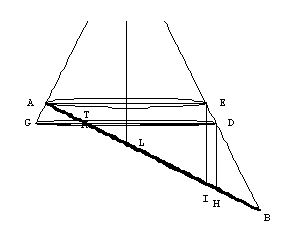
Now consider the similar triangles TAG and TDH in the plane through O, G, and D, the axial plane. The triangles are similar because they each have a right angle and opposite vertical angles. This in turn implies
|
|
|
|
or |
 |
|
|
(2) |
Also in the axial plane are the pairs of similar triangles HDT and IEA, and BDT and BEA. From these we see that
|
|
|
|
|
(3) |
|
|
(4) |
Combining (3) and (4) we have
|
|
|
|
|
(5) |
Notice also that in triangle IEA the line OL bisects AE so it must also bisect AI, making IA = 2AL. Putting this together with (1) and (2) we have
|
|
(5) |
This might not look like an equation that we recognize, but if we let KT = y, the distance from the center of the ellipse to T be x, AB = 2a, and 2AL = p we have
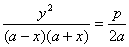

 .
.
This does look like the equation of an ellipse.
Gary S. Stoudt, "Can You Really Derive Conic Formulae from a Cone? - Deriving the Symptom of the Acute-angled Cone," Convergence (June 2015)

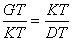 or
or
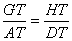
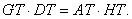
 or
or and
and .
. or
or .
.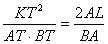 .
.


