- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Can You Really Derive Conic Formulae from a Cone? - Deriving the Symptom of the Ellipse
Apollonius, Conics, Book I, Proposition 13
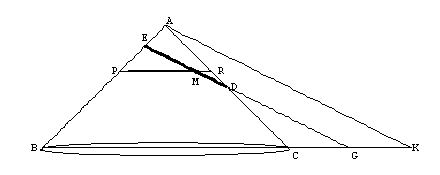
If a cone is cut by a plane through its axis, and also cut by another plane on the one hand meeting both sides of the axial triangle, and on the other extended neither parallel to the base nor subcontrariwise, and if the plane the base of the cone is in, and the cutting plane meet in a straight line perpendicular either to the base of the axial triangle or to it produced, then any straight line which is drawn from the section of the cone to the diameter of the section parallel to the common section of the planes, will equal in square some area applied to a straight line to which the diameter of the section has the ratio that the square on the straight line drawn from the cone's vertex to the triangle's base parallel to the sections's diameter has to the rectangle contained by the intercepts of this straight line (on the base) from the sides of the triangle, an area having as breadth the straight line cut off on the diameter beginning from the section's vertex by this straight line from the section to the diameter, and deficient (έλλειπου) by a figure similar and similarly situated to the rectangle contained by the diameter and parameter. And let such a section be called an ellipse (έλλειψις). We will still consider the cone with vertex A and a plane through the axis intersecting the cone. This plane intersects the cone in the axial triangle ABC, where BC is the diameter of the base circle of the cone.
 |
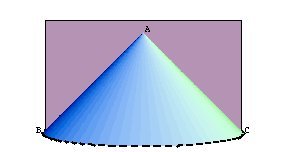 |
 To generate the ellipse the cutting plane must intersect both sides of the axial triangle. Once again this works for all cones in general, but we illustrate here with a right circular cone.
To generate the ellipse the cutting plane must intersect both sides of the axial triangle. Once again this works for all cones in general, but we illustrate here with a right circular cone.
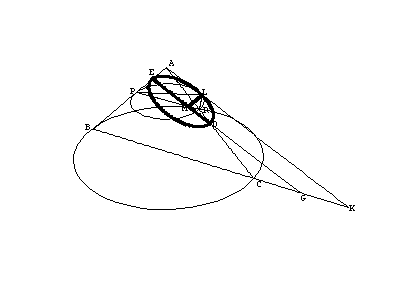
A dynamic view of this construction will be helpful in what follows.
 |
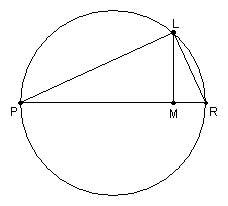 |
Consider an arbitrary ordinate (i.e. y value) ML constructed on the axis at M. We wish to determine the relationship between ML and EM, that is, the symptom of the conic. The ordinate ML is located in a horizontal plane that cuts the cone in the circle with diameter PR. In this horizontal plane construct the segments PL and LR, which results in a right triangle inscribed in a semicircle. As we saw before in the case of the parabola, by similar triangles this implies
|
|
|
|
|
(1) |
Apollonius next constructs a segment EH, perpendicular to DE, such that
|
|
(2) |  |
where AK is parallel to ED. [As in the previous section, all the lengths DE, AK, BK, and KC are known. He is simply finding the point H that makes the ratio true.]
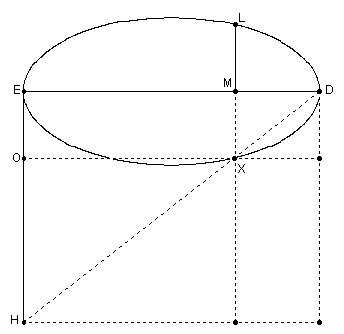
Notice in the figure that triangles DEH and DMX are similar. This implies that
|
|
(3) |
where the first equality is due to the similarity, and the second one is due to the fact that MX = EO. Next, consider the cone diagram carefully (a different viewpoint is below). The triangles ABK, EBG, and EPM in the axial plane are all similar (parallel lines), and also the triangles ACK, DCG, and DMR are all similar (do you see why?). From these two sets of similar triangles we have
|
|
(4) |
|
and |
 |
|
|
(5) |
Combining (2), (4), and (5) gives us
|
|
(6) |
Now compare (3) and (6) and notice that they imply PM . MR = EM . EO. However, from (1) we have ML2 = PM . MR, so together we have ML2 = EM . EO.
Taking another look at our ellipse, notice that triangles DEH and XOH are similar. This implies
|
|
|
|
|
 |
|
|
(7) |
Notice that EO = EH - HO, so ML2 = EM . EO becomes, using (7),
|
|
(8) |
In this form we can understand Apollonius' use of the word ellipse for this section. He has proven that the square on ML is equal to a rectangle applied to a line HE with a width equal to EM and deficient (ellipsis) by a rectangle similar to one contained by ED and HE.
Equation (8) is also the form that will enable us to see this as the modern form of an ellipse. Let y = ML, x = EM, p = HE, and ED = 2a. Substituting into (8) we have
|
|
Can this be written in the standard form of an ellipse? Complete the square and see.
In the next section we derive the symptom of the hyperbola. The derivation follows that of this section. You will notice very little difference between the two until the very end. In Apollonius's Conics, propositions concerning the ellipse and the hyperbola are frequently proven together, due to their similarities.
Gary S. Stoudt, "Can You Really Derive Conic Formulae from a Cone? - Deriving the Symptom of the Ellipse," Convergence (June 2015)

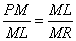 or
or .
.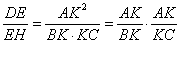 ,
,

 .
. .
.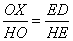

 .
.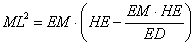 .
. .
.


