- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Converting the Old Babylonian Tablet ‘Plimpton 322’ into the Decimal System as a Classroom Exercise: Appendix – Classroom Exercise on Interpreting a Table Inspired by Plimpton 322
Setting: Convergence co-editor Amy Ackerberg-Hastings used this exercise at the beginning of the second class meeting of a 100-level general-education course offered by a community college physical sciences department on the History of Science. Enrollees were generally looking for a way to meet their science requirement with a minimum of mathematics and lab work, while the department encouraged the use of teaching through hands-on activities. Trade-offs between historical accuracy and mathematical/scientific principles communicated at levels accessible to the students tended to favor the latter.
Rationale: She wanted to begin the course with an experience of how historians make sense of the past. Other objectives included conveying some of the unique challenges involved in writing the history of ancient mathematics and science (ideally, without worsening students’ anxieties about mathematics); showing how Western science has been built upon a deep foundation; and introducing one of the course themes, the nature and evolution of scientific methods.
Activity: Divide students into groups of 3–4 and distribute a copy of the following table. Instruct the groups to try to figure out the relationship(s) between the numbers in each row. Allow about 10 minutes for discussion.
| \(\frac{25}{16}\) | 3 | 5 | 1 |
| \(\frac{169}{144}\) | 5 | 13 | 2 |
| 1 | 1 | \(\sqrt{2}\) | 3 |
| 2 | 2 | \(\sqrt{8}\) | 4 |
| 3 | 3 | \(\sqrt{18}\) | 5 |
| 2 | 1 | \(\sqrt{5}\) | 6 |
| 3 | 2 | \(\sqrt{13}\) | 7 |
| 5 | 4 | \(\sqrt{41}\) | 8 |
Table of Pythagorean values, organized as on Plimpton 322.
Debriefing Session: Reconvene, and ask for a report from each group. Explain that the table contains values that satisfy the Pythagorean Theorem, \(a^2+b^2=c^2\), although they have been rearranged and \(b\) is only denoted indirectly. See the table with headings on the slide below. Students were generally most surprised and annoyed with themselves to realize they did not realize that the column on the right contained row numbers.
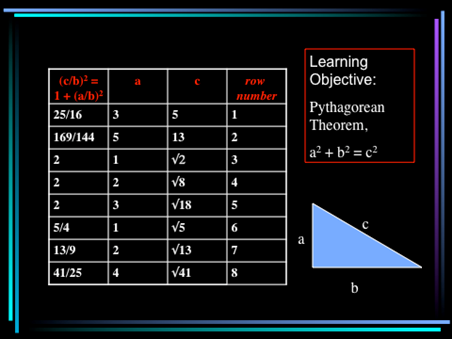
Classroom slide adding headings for the table used in the exercise.
Finally, Plimpton 322 (ca 1900–1600 BCE) can be introduced and briefly placed in the context of Mesopotamian science:
- Unlike the decimal numbers familiar to us and utilized in our exercise, the Mesopotamians used a sexagesimal numeral system.
- Mesopotamians wrote records on clay tablets with number symbols made from impressing wedges.
- The Mesopotamians used mathematical astronomy for agriculture and religion and astrology and setting a calendar, and they mapped the fixed stars and planets. They also left many clay tablets showing commercial transactions and problems sets for students.
- The Greeks believed that mathematics originated in Egypt and Mesopotamia.
Leave the students with questions such as: Is a list of examples scientific? How do historians figure out the history of ancient science? The debriefing and mini-lecture takes about 15–20 minutes, so that the entire activity requires around 30 minutes of in-class time.
As noted above, the students enrolled in the history of science course for which the activity was developed were nearly all subconsciously or overtly math-phobic, so Ackerberg-Hastings eventually simplified the table further to provide values for b in the left column instead of the \((c/b)^2+1=(a/b)^2\) that better corresponds to Plimpton 322. See the attached 2-part handout, which also features hints. Students were only slightly more successful at solving the puzzle, although they seemed to enjoy taking a few minutes to wrestle with it.
Follow-up: As homework, students can be assigned the following writing prompt:
Write a report (100–150 words) on the experiment in today’s class. Discuss how your group tried to determine the relationships between the numbers in the table, how your conclusions compared with those drawn by historians of Old Babylonian mathematics and astronomy, and the insights you gained into the history of science through this activity.
Antonella Perucca (University of Luxembourg) and Deborah Stranen (University of Luxembourg), "Converting the Old Babylonian Tablet ‘Plimpton 322’ into the Decimal System as a Classroom Exercise: Appendix – Classroom Exercise on Interpreting a Table Inspired by Plimpton 322," Convergence (October 2020)




