Cuisenaire Art: Modeling Figurate Numbers and Gnomonic Structures - More Polygonal Numbers

Theory of Polygonal Numbers

Figurate numbers whose "figures" are regular polygons, such as triangular numbers and square numbers, are also known as polygonal numbers. Prior to the modeling of the pentagonal and hexagonal numbers using the Cuisenaire rods, students in groups first studied the excerpt on the theory of polygonal numbers, credited to Nicomachus, from Thomas Heath's A History of Greek Mathematics: From Thales to Euclid (1921):

The gnomons of triangles are therefore the successive natural numbers. Squares are obtained by adding any number of successive terms of the series of odd numbers, beginning with \(1,\) or \[1,\,\,3,\,\,5,\,\,\dots,\,2n-1,\dots.\] The gnomons of squares are the successive odd numbers. Similarly the gnomons of pentagonal numbers are the numbers forming an arithmetical progression with \(3\) as common difference, or; \[1,\,\,4,\,\,7,\,\,\dots,\,1+(n-1)\cdot3,\dots;\] and generally the gnomons of polygonal numbers of \(a\) sides  are \[1,\,\,1+(a-2),\,\,1+2(a-2),\,\,\dots,\,1+(n-1)(a-2),\dots\] and the \(a\)-gonal number with side \(n\) is \[1+1+(a-2)+1+2(a-2)+\cdots +1+(n-1)(a-2)=n+{\frac{1}{2}}n(n-1)(a-2).\] The general formula is not given by Nicomachus, who contents himself with writing down a certain number of polygonal numbers of each species up to heptagons. (p. 106)

This summative activity proved beneficial in that students appeared to excel in their understanding of the word “gnomon.” Some groups went back to the exploration of the triangular numbers and explained that every Cuisenaire rod in the formation of a triangular number could be thought of as a gnomon whose combination produces the triangular number itself: Gnomons of triangular numbers are consecutive positive integers. For instance, the gnomons of the triangular number 10 are 1, 2, 3, and 4.

Gnomons of Pentagonal Numbers

Nicomachus wrote that any square number is the sum of two consecutive triangular numbers and (without modern notation) that

an \(a\)-gonal number of side n is the sum of an \((a-1)\)-gonal number of side \(n\) plus a triangular number of side \((n-1),\) i.e. \[n+{\frac{1}{2}}n(n-1)(a-2)=n+\frac{1}{2}n(n-1)(a-3)+\frac{1}{2}n(n-1)\quad{\sf{\small{(1921, p. 106).}}}\]

Letting \(a=5\) in the first half of Nicomachus' theorem, students obtained that a pentagonal number of side \(n\) is the sum of a square number of side \(n\) plus a triangular number of side \(n-1.\) From this, together with the template given in the text (see Figure 12a), students then came up with a diversity of visualizations of the pentagonal number sequence using the Cuisenaire rods (see Figures 12b-f).

• Whereas Figures 12b and 12c model every \(n\)th pentagonal number as a combination of the \(n\)th square number and the \((n-1)\)th triangular number, Figure 12d shows every \(n\)th pentagonal number as decomposed into three structures: the \(n\)th positive integer, plus the \((n-1)\)th oblong number, plus the \((n-1)\)th triangular number.
• Using the fact that any oblong number can be decomposed into two congruent triangular numbers at the same level, the arrangement from Figure 12d was slightly modified to obtain the arrangement that contains three sets of \((n-1)\)th triangular numbers along with the Cuisenaire rod modeling the \(n\)th positive integer (see Figure 12e).
• Finally, Figure 12f shows that every \(n\)th pentagonal number is made of the \(n\)th triangular number and the \((n-1)\)th oblong number.

	a (1921, p. 79)
	b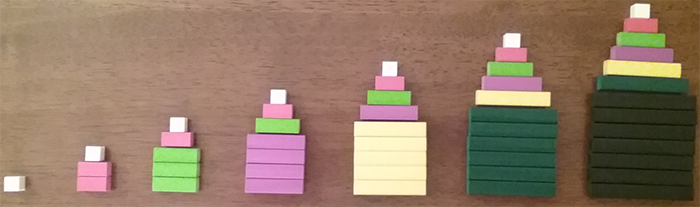
	c
	d
	e
	f

Figure 12:  Pentagonal numbers 1, 5, 12, 22, 35, 51, 70 with Cuisenaire rods

Gnomons of Hexagonal Numbers

Letting \(a=6\) in the first half of Nicomachus' theorem, students obtained that a hexagonal number of side \(n\) is the sum of a pentagonal number of side \(n\) plus a triangular number of side \(n-1.\) From this, together with the template given in the text (see Fig. 13a), students then came up with a diversity of visualizations of the pentagonal number sequence using the Cuisenaire rods (see Figures 13b-f).

• Whereas Figures 13b and 13c model every \(n\)th hexagonal number as a combination of the \(n\)th pentagonal number and the \((n-1)\)th triangular number, Figure 13d models an equivalent arrangement: every \(n\)th hexagonal number is made of the \(n\)th square number and two sets of \((n-1)\)th triangular numbers.
• Using the fact that two congruent triangular numbers are equivalent to the oblong number at the same level (see Figure 9b), an alternative arrangement is obtained as follows: every \(n\)th hexagonal number is made of the \(n\)th square number and the \((n-1)\)th oblong number (see Figure 13e).
• Figure 13f shows another equivalent form of Theon’s Theorem (see Figure 10b) as follows: Because the \(n\)th square number can be decomposed into the sum of the \(n\)th triangular number and the \((n-1)\)th triangular number, we obtain: every \(n\)th hexagonal number consists of the \(n\)th triangular number and three sets of \((n-1)\)th triangular numbers (see Figure 13f).
• Equivalently, by decomposing the \(n\)th triangular number into an \((n-1)\)th triangular number plus \(n,\) we can express every \(n\)th hexagonal number as the combination of four sets of \((n-1)\)th triangular number plus a Cuisenaire rod modeling the integer \(n\) (see Figure 13g); which is equivalent to the combination of two sets of \((n-1)\)th oblong numbers plus \(n\) (see Figure 13h).
• This arrangement also reveals the fact that every \(n\)th hexagonal number can be arranged as an \(n\times(2n-1)\) rectangle. Further decomposition yields the interesting result that every \(n\)th hexagonal number is equal to the combination of two sets of \((n-1)\)th triangular numbers plus the \((n-1)\)th oblong number plus a Cuisenaire rod modeling the integer n (see Figure 13i).
• Finally, a triangular staircase arrangement of hexagonal numbers yields the well-known fact that every hexagonal number is indeed a triangular number – the \((2n-1)\)th triangular number (see Figure 13j).

	a (1921, p. 79)
	b
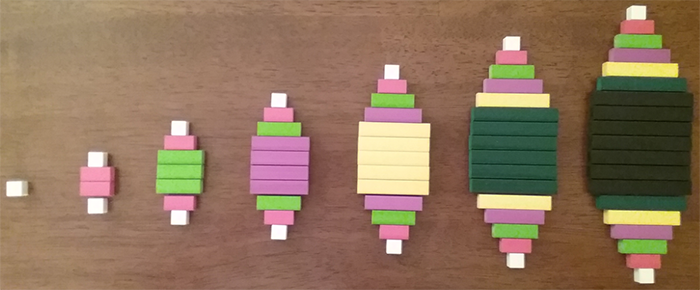	c
	d
	e
	f
	g
	h
	i
	j

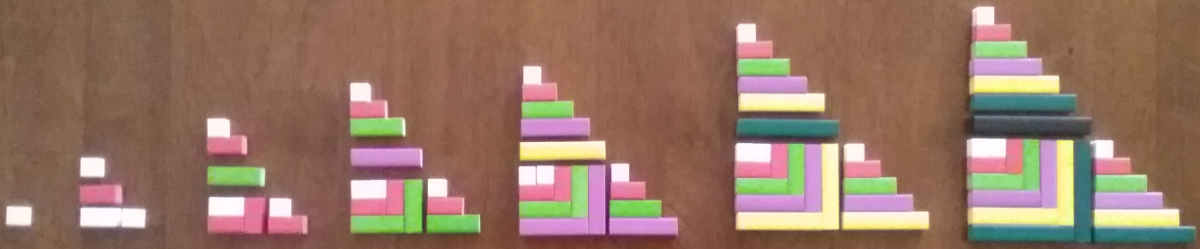Figure 13:  Hexagonal numbers 1, 6, 15, 28, 45, 66, 91 with Cuisenaire rods