- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Dear Professor Greitzer - Slopes of Lines and Angles of Inclination
We began with an exploration of the relationship between the slopes of lines and the angles of inclination that they make with a horizontal axis. After some rather non-precise measurements with a protractor, we used Geometer’s Sketchpad to explore further (see Figure 1), and built a table of values precise to the nearest tenth of a degree. Relevant parts of the table are found in Chart 1.

Figure 1

Anytime we collect data, we stare at it, looking for patterns. For some in our classes, the observation that the 45o entries are collinear is a revelation. But, every now and again, we get deeper results, and one year a student remarked that the angles associated with slopes of 1/2 and of 1/3 (26.6o and 18.4o, respectively) appeared to give a sum of 45 degrees. We changed the preferences on Sketchpad to explore more significant digits and this conjecture seemed to hold. That gave us the open door from the inductive living room to the deductive kitchen, and in our best Euclid voice, we asked, “Why?”
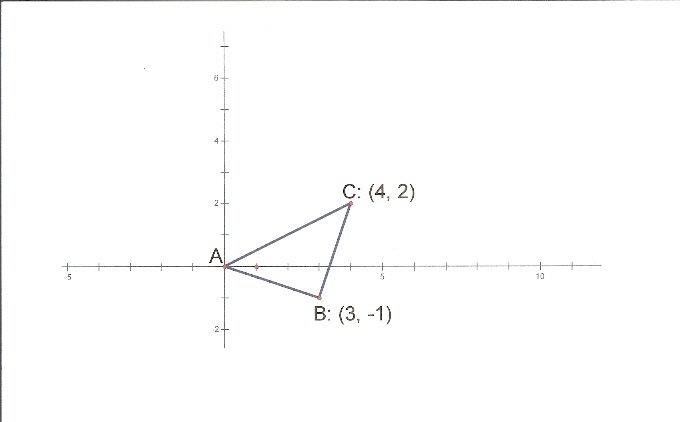
Figure 2
Figure 2 illustrates why. The triangle is clearly a right triangle (legs have negative reciprocal slopes) and is isosceles as well (leg lengths are each the square root of 10). The 45-degree angle at the origin has been split into two angles by the x-axis. The segment below the x-axis, connecting A(0,0) and B(3,-1) has a slope of negative 1/3. Similarly, the segment above, connecting A(0,0) and C(4,2) has a slope of 2/4 = 1/2. Done.
Joe Richards and Don Crossfield, "Dear Professor Greitzer - Slopes of Lines and Angles of Inclination," Convergence (July 2010)




