- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Dear Professor Greitzer - The Second Identity
On to the second identity, which was that
$${\frac{\pi}{4}}=4\arctan{\frac{1}{5}}-\arctan{\frac{1}{239}} \quad {\rm !!!}$$
Looking back at Chart 1, we observed that the angle associated with a slope of 4/3 appeared to be twice that of the angle that goes with a slope of 1/2. Exploring that possibility led to the picture in Figure 4.
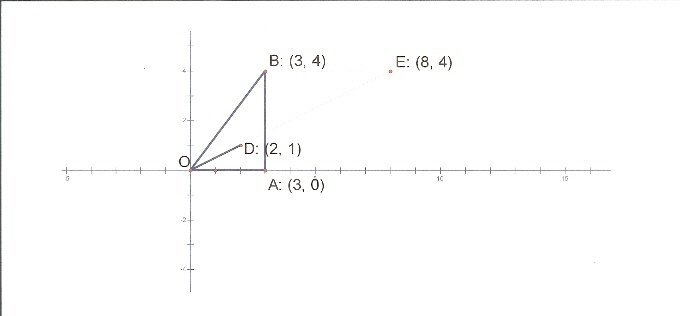
Figure 4
Triangle OAB is a 3-4-5 triangle, with segment OB having a slope of 4/3. Segment OD has slope 1/2 and our conjecture was that it bisected angle AOB. We extended OD until its endpoint, called E, was horizontally to the right of B, and observed happily that the length of segment BE was also 5. Therefore triangle BEO was isosceles. The students also noted that angles BEO and EOA were alternate interior angles of parallel line segments. Since angle BEO was equal to each of angles BOE and AOE, the latter two angles were equal and we were done.
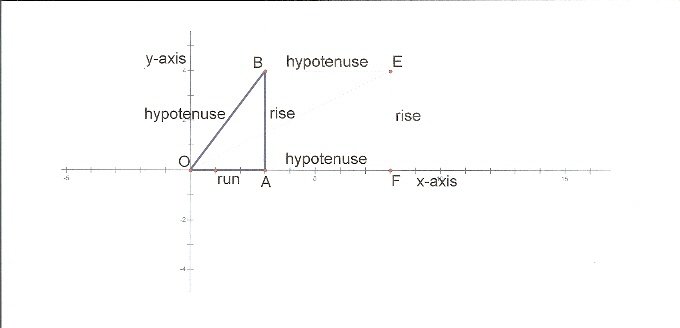
Figure 5
Figure 5 is the generalized version of Figure 4. Notice that angle EOF is half of angle BOA, and that the slope of angle EOF is the fraction
|
This let us build Chart 2.
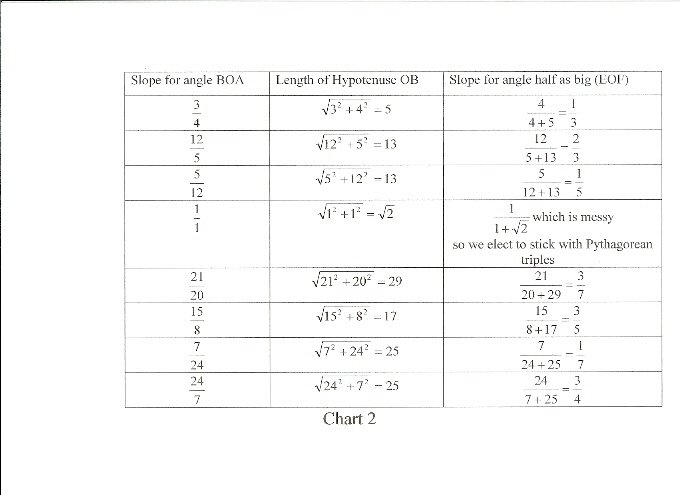
While the students happily constructed entries, a few clever ones noticed from the top row that 2arctan(1/3) = arctan(3/4) and from the bottom row that 2arctan(3/4) = arctan(24/7), from which one may conclude that 4arctan(1/3) = arctan(24/7).
This struck us (teachers) as looking a bit like the identity (!!!). If only we wanted the value of arctan(24/7). What we really wanted, to make some headway in (!!!), was the value of arctan 1 ... and we didn’t actually want it; we knew it was 45o. What we wanted was an expression equivalent to it, in terms of slopes of smaller angles. It occurred to us to bisect, twice, the 45-degree angle. It then occurred to us that we tried that in Chart 2 and since 1-1-\(\sqrt 2\) isn’t a Pythagorean Triple, we got messy numbers very quickly. A happy compromise would be to find a practically isosceles right triangle, whose sides form a Pythagorean triple. Twice bisecting this practically 45-degree angle will give us practically what we want, and perhaps we can adjust later (do you hear the sound of arctan(1/239)?).
Practically isosceles right triangles, hmmm... the only ones with legs that are consecutive integers that are commonly known in our math circles are 3-4-5, 20-21-29, and 119-120-169. One can use natural number values of m and n in the expressions m2 - n2, 2mn, and m2 + n2 to generate Pythagorean Triples, and the pairs (m=2, n=1), (m=5, n=2), and (m=12, n=5) generate those triples above.
Joe Richards and Don Crossfield, "Dear Professor Greitzer - The Second Identity," Convergence (July 2010)




