- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Discovery of Huffman Codes
Introduction
|
|
 |
 |
Figure 1. David Huffman in 1978 and in 1999 (both photos courtesy of University of California, Santa Cruz)
The story of the invention of Huffman codes is a great story that demonstrates that students can do better than professors. David Huffman (1925-1999) was a student in an electrical engineering course in 1951. His professor, Robert Fano, offered students a choice of taking a final exam or writing a term paper. Huffman did not want to take the final so he started working on the term paper. The topic of the paper was to find the most efficient (optimal) code. What Professor Fano did not tell his students was the fact that it was an open problem and that he was working on the problem himself. Huffman spent a lot of time on the problem and was ready to give up when the solution suddenly came to him. The code he discovered was optimal, that is, it had the lowest possible average message length. The method that Fano had developed for this problem did not always produce an optimal code. Therefore, Huffman did better than his professor. Later Huffman said that likely he would not have even attempted the problem if he had known that his professor was struggling with it.
|
|
 |
 |
Figure 2. Robert Fano in 1975 and in 2012 (both photos courtesy of MIT and Robert Fano; for the photo at left, see [1])
The project, "Discovery of Huffman Codes," uses excerpts from Fano’s work ([2]) and from Huffman’s paper ([3]), where they present their encodings. Both Fano and Huffman used greedy strategies to find the codes. However, Fano’s greedy algorithm would not always produce an optimal code while Huffman’s greedy algorithm would always find an optimal solution. The purpose of the project is for students to learn greedy algorithms, prefix-free codes, Huffman encoding, binary tree representations of codes, and the basics of information theory (unit and amount of information). The project demonstrates that a greedy strategy could be applied in different ways to the same problem, sometimes producing an optimal solution and sometimes not.
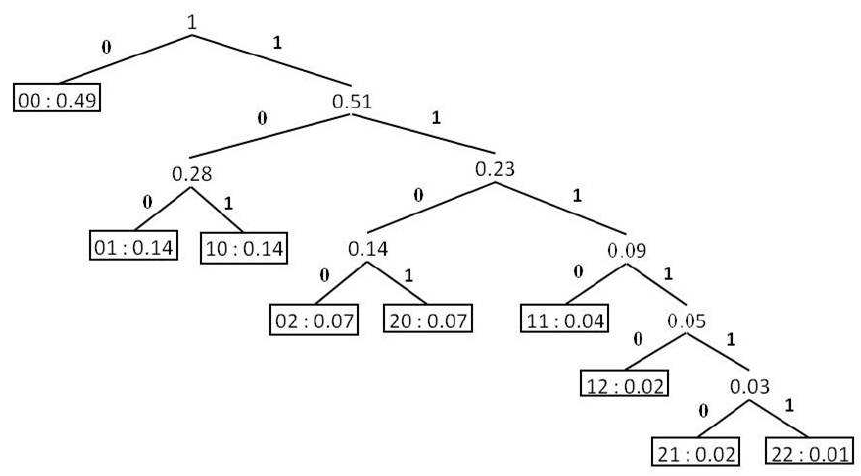
Figure 3. Binary tree representation of codes for messages 00, 01, 10, 02, 20, 11, 12, 21, and 22 with probabilities 0.49, 0.14, 0.14, 0.07, 0.07, 0.04, 0.02, 0.02, and 0.01, respectively.
The project, Discovery of Huffman Codes, is ready for students, and the Latex source is also available for instructors who may wish to modify the project to better suit their needs. The “Notes to the Instructor” presented next are also appended to the project itself.
Our primary source project module for students is part of a larger collection published in Convergence. For more projects, see Primary Historical Sources in the Classroom: Discrete Mathematics and Computer Science.
Notes to the Instructor
This project is designed for a junior-level Data Structures and Algorithms course. It can be used when covering the topic of greedy algorithms. The project uses excerpts from Fano’s and Huffman’s papers ([2], [3]) to explore greedy algorithms, prefix-free codes, Huffman encoding, binary tree representations of codes, unit and amount of information.
The project is divided into several sections. Each section, except for the Introduction, contains a reading assignment (read selected excerpts from the original sources and some additional explanations) and a list of exercises on the material from the reading. Exercises are of different types, some requiring simple understanding of a definition or an algorithm, and some requiring proofs. Exercises 2.8, 4.10, and 5.1 are programming exercises and require good programming skills.
The material naturally splits into two parts. The first part (sections 1 and 2) is based on Fano’s paper ([2]). It introduces measuring information and Fano encoding. Students may need substantial guidance with this part. The second part (sections 3, 4, and 5) is based on Huffman’s paper ([3]). Sections 3 and 4 discuss Huffman encoding and compare it to Fano’s. Section 5 can be skipped as it describes a generalization of Huffman’s method to the case in which three or more digits are used for coding. Each of the two parts can be used as a one-week homework assignment, which students can complete individually or in small groups. For instance, the first assignment may ask students to read sections 1 and 2 and do exercises 2.1-2.10. The second assignment may ask students to read sections 3 and 4 and do exercises 3.1-3.4 and 4.1-4.11 (section 5 is skipped).
Download the project Discovery of Huffman Codes as a pdf file ready for classroom use.
Download the modifiable Latex source file for this project.
For more projects, see Primary Historical Sources in the Classroom: Discrete Mathematics and Computer Science.
References
[1] Massachusetts Institute of Technology Laboratory for Computer Science Brochure, 1975: http://groups.csail.mit.edu/medg/people/psz/LCS-75/social.html Retrieved 11/14/2014.
[2] R. M. Fano. The transmission of information. Technical Report 65, Research Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, Massachusetts, 1949.
[3] David A. Huffman. A method for the construction of minimum-redundancy codes. Proceedings of the Institute of Radio Engineers, 40(9): 1098–1101, September 1952.
Acknowledgment
The development of curricular materials for discrete mathematics and computer science has been partially supported by the National Science Foundation’s Course, Curriculum and Laboratory Improvement Program under grants DUE-0717752 and DUE-0715392 for which the authors are most appreciative. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Inna Pivkina (New Mexico State University), "Discovery of Huffman Codes," Convergence (July 2015)




