- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Exploring Liu Hui’s Cube Puzzle - Historical Review of Liu Hui's Cube Dissection
Figure 2. A cube is dissected, using Liu Hui's approach, into three solids that are \({\frac{1}{2}}, {\frac{1}{3}},\) and \({\frac{1}{6}}\) of its volume. To see the dissection from different perspectives, click then drag the image below.
Liu Hui (刘徽, ca. 220 AD – ca. 280 AD) was a third-century Chinese mathematician, well known as the “Euclid of China” for his dominant contributions to Chinese mathematics (Dauben, 2007). Although little is known today about his personal life, Liu Hui is widely recognized for his original commentaries on the ancient Chinese mathematical text, Jiu Zhang Suan Shu or the Nine Chapters on the Mathematical Art, which laid the foundation for the development of Chinese mathematics (Li & Du, 1987). Over time, Liu Hui's commentaries were further edited and annotated by successive mathematicians such as Li Chunfeng (李淳风, 602 – 672 AD) and Li Huang (李潢, ca.1746 – 1812). Thus, there are in existence various editions of this classic of Chinese mathematics (e.g, Liu & Li, n.d.; Li, 1820). In his commentaries, Liu Hui elaborated on 246 problems in nine chapters, covering a wide variety of mathematical ideas from arithmetic to matrix algebra, along with geometry in various real-world applications characteristic of his era, such as farming and earthworks.
In Chapter Five of Nine Chapters on the Mathematical Art, entitled Shang Gong (商功, construction consultations), Liu Hui commented on a series of 28 problems concerning the volumes of solids in the context of civil engineering and grain measurement. Here, Liu Hui may not have been as much interested in designing a puzzle as finding algorithms to calculate the volumes of various polyhedral solids. Problem 15 of Chapter Five is of special significance in our present case. The original problem, answer, and the corresponding rule in the Nine Chapters on the Mathematical Art are as follows (trans. Shen, Crossley & Lun, 1999, p. 269):
Now given a yangma, with a breadth of 5 chi, a length of 7 chi and an altitude of 8 chi. Tell: what is the volume? Answer: \(93{\frac{1}{3}}\) [cubic] chi. The Rule [for a yangma]: Multiply the breadth by the length, then multiply by the altitude, divide by 3.
The term yangma (阳马), which makes little sense nowadays in modern Chinese, is an ancient Chinese term for a special kind of rectangular pyramid. The term chi is a Chinese linear unit, still in limited use today with a modern definition. In ancient Chinese, chi was also used as a square unit and a cubic unit (as in the problem above), subject to the specific context. In his commentary on the problem above, Liu Hui detailed his method of cube dissection for finding the volume of a yangma. He started with a cube, which has three equal dimensions, and dissected it along two face diagonals, as described below (trans. Shen, Crossley, & Lun, 1999, p. 269):
Take a cube 1 chi in each of breadth, length and altitude. The product is 1 [cubic] chi. Cutting the cube on a diagonal gives two right triangular prisms (qiandu). Dissecting a right triangular prism (qiandu) on a diagonal gives a yangma and a bie'nao. The yangma occupies 2 parts and the bie'nao 1 part. These are fixed rates. Two bie'nao constitute 1 yangma, and 3 yangma constitute 1 cube.
Liu Hui's approach is clear once we get hold of a cube and perform the dissecting operations (see Figure 2, above). His use of terms, however, calls for some explanation.
- A qiandu (堑堵), meaning literally an embankment beside a trench, is a metaphoric term for a right triangular prism such as the green piece in Figure 2.
- A yangma (阳马) is the corner of a rectangular pyramid such as the red piece in Figure 2; it probably has its origin in architecture. Interestingly, in its Japanese explanation, yangma is called a “sunshine-carrying horse,” which in fact conveys part of its literal meaning in Chinese (四角錐, n.d.).
- A bie'nao (鳖臑), meaning literally a turtle's foreleg bone, is a metaphor for a tetrahedron with a right triangular base or, in short, a triangular pyramid such as the purple piece in Figure 2. However, in the context of the problem above, a bie'nao is taken to be a tetrahedron with four right triangular faces.
All three terms were essential in Liu Hui's efforts to find the volumes of polyhedral solids, although they do not make much sense in modern Chinese without further explanation. Therefore, they ought to be used with respect to Liu Hui's specific geometric dissections. The context will help readers understand the underlying mathematical processes and the resulting objects. About the terminology, Martzloff (1987/1997) suggested, "Whatever the exact etymologies, there is no doubt that here these terms have no more to do with architecture than terms like 'pyramid' used in a mathematical context" (p. 283). Indeed, Liu Hui may have just used these pieces as qi (棋, chess pieces) to make sense of other solids or to play games, hence the puzzle nature of Liu Hui's dissections (Martzloff, 1987/1999). As a further linguistic note, Chinese nouns do not have plural forms. Accordingly, in literal translations, their plural forms are the same as their singular forms, such as in the case of “3 yangma constitute 1 cube.”
It is noteworthy that Liu Hui's approach and his use of terms such as qiandu, yangma, and bie'nao are not restricted to cubes only but are applicable to any rectangular prism or rectangular parallelepiped. In fact, Liu Hui used lifang (立方, a rectangular prism) in the Chinese text. When he needed to specify a cube, he would give the lifang three equal dimensions. Therefore, it is important that we make sense of Liu Hui's approach in the context of arbitrary rectangular prisms and treat a cube as a special case (Wagner, 1979; Ying, 2011; Li, 2002). In English translations, an arbitrary rectangular prism (or rectangular parallelepiped) is sometimes called a (rectangular) box or cuboid. For a mathematical puzzle, a cube is more appropriate in light of its rich symmetries. When a cube is used, Liu Hui's approach leads to one type of qiandu, one type of yangma, and two types of bie'nao, depending on the choice of the second diagonal cut. The two types of bie'nao are mirror images of each other. It is visually evident that two congruent qiandu make a cube (see Figure 3) and three congruent yangma also make a cube (see Figure 4). In the case of a cube, therefore, it is fairly easy to see that a yangma is one third of the cube volume. Given six bie’nao, if three of them are mirror images of the rest, one can also make a cube (see Figure 5). Thus, a bie’nao is one sixth of the cube volume. These relationships can also be explored visually using dynamic models.

Figure 3. Two qiandu (triangular prisms) make a cube. To see the dissection from different perspectives, click then drag the image below.

Figure 4. Three yangma (triangular prisms) make a cube. To see the dissection from different perspectives, click then drag the image below.

Figure 5. Six bie'nao (triangular pyramids) make a cube after mirroring three of them. To see the dissection from different perspectives, click then drag the image below.
By contrast, an arbitrary rectangular prism is more complicated because it does not have all the symmetries of a cube. Consequently, Liu Hui's dissection leads to three types of qiandu, six types of yangma, and twelve types of bie'nao (with four right triangular faces), depending on the choice of both diagonals during the dissecting process. Three of the yangma are mirror images of the rest; six of the twelve bie'nao are mirror images of the rest (Shen, Crossley, & Lun, 1999, pp. 272-273). Figure 6 shows Liu Hui's dissection of an arbitrary rectangular prism, where the green piece is a qiandu (1/2 of the rectangular prism), the red piece is a yangma (1/3 of the rectangular prism), and the purple piece is a bie'nao (1/6 of the rectangular prism). Figure 7 further shows three ways to dissect the same rectangular prism, each way yielding a distinct qiandu, yangma, and bie'nao. The three yangma in Figure 7 have distinct bases, and they can be assembled to form the original rectangular prism (Figure 8). Their mirror images also form the original rectangular prism in a different orientation. As can be seen, Liu Hui's approach seems to apply to all arbitrary rectangular prisms as well as to a cube.

Figure 6. Liu Hui's dissection of an arbitrary rectangular prism into a quiandu (green piece), a yangma (red piece), and a bie'nao (purple piece).
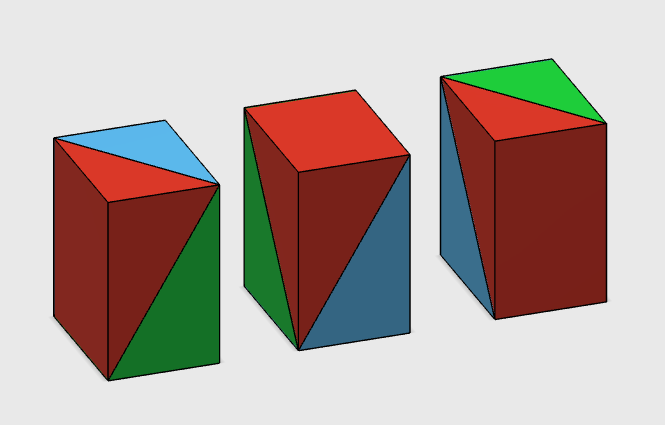
Figure 7. Three different dissections of an arbitrary rectangular prism that yield three distinct quiandu, yangma, and bie'nao. The blue pieces are quiandu, the red pieces yangma, and the green pieces bie'nao.

Figure 8. Three distinct yangma can be assembled into the original rectangular prism.
But, in the general case, does each yangma (rectangular pyramid) have the same volume? If so, what is that volume? Liu Hui did not answer these questions directly using the visual method in Figure 8, but instead set out to show that there is a 2-to-1 ratio between the volumes of a yangma and a bie'nao. Given that the qiandu has half the volume of the rectangular prism, this 2-to-1 ratio of the volume of the yangma to that of the bie'nao would then guarantee volumes of \({\frac{1}{2},} {\frac{1}{3},} \) and \({\frac{1}{6}}\) of the volume of the rectangular prism for, respectively, the qiandu, yangma, and bie'nao.
Lingguo Bu (Southern Illinois University Carbondale), "Exploring Liu Hui’s Cube Puzzle - Historical Review of Liu Hui's Cube Dissection," Convergence (January 2017)





