- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Exploring Liu Hui’s Cube Puzzle - In the Classroom: Paper Folding and GeoGebra Construction
GeoGebra is a free and open-source software environment for mathematical modeling, available at www.geogebra.org for all major computing platforms. Initially, I planned to design some flexible templates for prospective teachers to build the three solids in Liu Hui's Cube Puzzle and further use them as motivation to discuss multiple modes of student engagement in mathematics teaching. GeoGebra proves adequate for this purpose. After defining an independent variable for the length of a cube edge, one can construct the three templates using the line and circle tools in GeoGebra, paying attention to the various right triangles that form the faces of the three solids (Figure 12). To facilitate assembly and subsequent discussions, each template should be printed on a letter-sized cardstock sheet of a distinct color. For example, in Figure 13, the qiandu (triangular prism) is in green, the yangma(rectangular pyramid) is in red, and the bie'nao (triangular pyramid) is in purple. In the beginning, students have little knowledge of the fractional relationships among the three solids. Therefore, it is pedagogically advisable to refer to them as the green, red, or purple pieces.
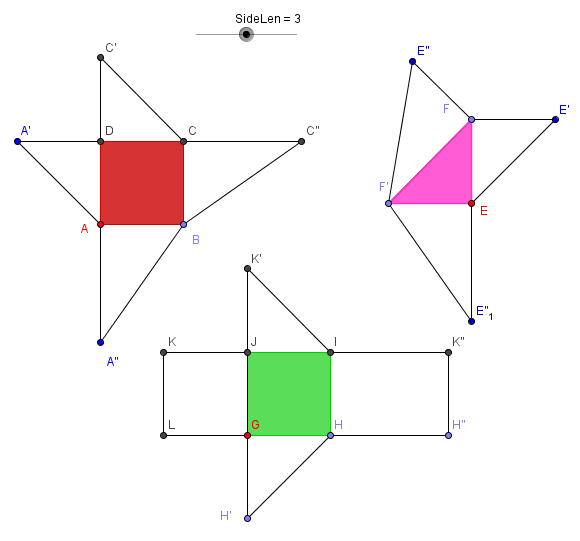
Figure 12. Templates for the three component solids of Liu Hui's Cube Puzzle designed with GeoGebra. Download all three templates here.
Figure 13. The three solids constructed by students from cardstock paper templates—from left to right: a yangma, a bie'nao, and a qiandu.
In light of its rich mathematical structure, Liu Hui's Cube Puzzle allows for various forms of student interaction. To begin with, each student will cut out and assemble (using adhesive tape) all three solids. Then students should be directed to work individually to try to put the three pieces together to make a shape with which they are familiar. Some students may make something other than a cube, which is perfectly acceptable. Some students will eventually produce a cube to their own amazement. Gradually, the whole class will catch up as students help each other or watch others solve the puzzle.
The game is not over yet. Next, the instructor could ask students to work in groups of two, using only the green (qiandu) solids, and see if they can make a cube (Figure 14). A question about the volume of the green piece (qiandu) naturally follows. If two green pieces (qiandu) make a whole cube, its volume is one half of the cube. Subsequently, students will work in groups of three, using three red pieces (yangma) and try to put them together in a cube (Figure 15). They may have to try a few times before settling on a cube, which is part of the instructional plan. If three red pieces (yangma) make a cube, then one piece (yangma) must be one third of the cube in terms of its volume.
The last task is more challenging and is also more interesting. Students will now work in groups of six, using six purple pieces (bie'nao). They may initially have trouble putting the blocks together in a cube because they don't seem to fit in with each other. Some students will try to make a red (yangma) piece using two purple ones (bie'nao), but cannot get the orientation correct. Depending on the instructional objectives, the instructor could make a suggestion at this moment that the purple one (bie'nao) can be folded backward, thus making a mirror image of the original bie’nao. The original and mirrored ones will fit nicely in a red piece (yangma). The rest will be straightforward, because three yangma make a cube, as is already known. After mirroring three of the six purple pieces (bie'nao), each group will be able to make three red pieces, which form a cube (Figure 16).

Figure 14. Two qiandu (triangular prisms) make a cube.

Figure 15. Three yangma (triangular prisms) make a cube.

Figure 16. Six bie'nao (triangular pyramids) make a cube after mirroring three of them.
Liu Hui's Cube Puzzle provides multiple opportunities for students to work with each other in collaborative groups while they reason repeatedly about the mathematical relationships among the three polyhedral solids. A few beautiful observations will surface after the group work: \[\frac{1}{2}+\frac{1}{3}+\frac{1}{6}=1,\,\,\, \frac{1}{2}=\frac{1}{3}+\frac{1}{6},\,\,\,{\rm{and}}\,\,\, \frac{1}{3}=\frac{1}{6}+\frac{1}{6}.\] It is eye-opening for the students to experience these amazing connections between geometric objects and between geometry and arithmetic. The cube puzzle construction task can be used across the grades to facilitate students' mathematical exploration and sense-making for various instructional goals. Students may initially have difficulty using the various terms, whether they are English translations, numeric descriptions, or original Chinese names. Pedagogically, colors are useful for smooth communication at the beginning of the activities. Even Liu Hui had to use red and black colors to explore the relationships in his cube dissection. As students get to know the processes involved, other names may naturally surface in the classroom discussions. Otherwise, these terms should be introduced at an appropriate moment. Eventually, students will realize that, for example, the red piece, whose volume is one-third of the cube, is called a rectangular pyramid in English and it is called a yangma in ancient Chinese. The struggle with linguistic references is a healthy one in an educational context.
Pedagogically, the paper-based activities described above may take up to two hours. During the first hour, students will make the three solids from paper templates and explore their relationships in an open manner. During the second hour, students will conjecture, articulate, and justify the specific relationships among these solids with respect to each other and the whole cube. Alternatively, the construction task can be assigned as homework. When students bring ready-made solids to class for discussion, the whole activity may be implemented in one hour. Further extensions, as described on the next two webpages, can be considered at the discretion of the instructor in accordance with student need and curricular goals.
Lingguo Bu (Southern Illinois University Carbondale), "Exploring Liu Hui’s Cube Puzzle - In the Classroom: Paper Folding and GeoGebra Construction," Convergence (February 2017)





