- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Extending al-Karaji's Work on Sums of Odd Powers of Integers - Introduction
The purpose of this article is to share a general method of finding sums of odd powers of integers. This method is based on an idea originally due to Abu Bakr al-Karaji, who worked in Baghdad around the year 1000 CE (or AD). Our source is an article published in 1867 in the first volume of the first Turkish mathematics journal, Mebahis-i ilmiyye (Scientific Themes). Gunergun (2007) first introduced us to Mebahis-i ilmiyye in her article, "An early Turkish journal on mathematical sciences: Mebahis-i İlmiyye," in which she described the contents of the two volumes (10 issues each) of the journal. When we saw that the journal contained an article on sums of odd powers of integers, we set out to find a copy. After a few visits to rare book stores, we found an original copy of Mebahis-i İlmiyye in good condition.
When we opened the journal to the article on sums of odd powers, we found the well-known formula for the sum of the cubes of the first n positive integers, \[ 1^3 + 2^3 + 3^3 + \cdots + n^3 = {{(1+2+3+\cdots +n)}^2},\] here attributed to al-Karaji.
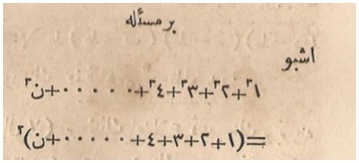
Figure 1. Sum of cubes formula (from Mebahis-i İlmiyye, 1867, courtesy of the authors).
Be sure to read the identity in Figure 1 from right to left. The last integer in each sum, at the far left, is the Arabic (and Hebrew) letter Nun or N. The word at the top could be translated into English as “a problem” or “a question,” and the word at upper right means “that is” or “this is.” The Arabic numerals appear in the table in Figure 2.

Figure 2. Arabic numerals \( 0\) – \( 9.\)
Hakan Kursat Oral (Yildiz Technical University) and Hasan Unal (Yildiz Technical University), "Extending al-Karaji's Work on Sums of Odd Powers of Integers - Introduction," Convergence (August 2011), DOI:10.4169/loci003725




