- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Fermat’s Method for Finding Maxima and Minima: A Mini-Primary Source Project for Calculus 1 Students
Whether it’s John Adams vs. Thomas Jefferson, or Will Smith vs. Chris Rock, few things capture our attention like a good argument.1 A fantastic example of such a feud arose in the 17th century between two mathematical greats—Pierre de Fermat (1601–1665) and René Descartes (1596–1650)—around a central theme of today’s introductory calculus courses. The mini-Primary Source Project (mini-PSP) Fermat’s Method for Finding Maxima and Minima uses the Fermat vs. Descartes disagreement as an engaging and welcoming point of entry to building a deeper understanding of today’s optimization technique by comparing it with Fermat’s original, more algebraic framework for finding extrema of functions. While students might be initially confused about optimization methods, they don’t need to feel this is an indication that they don’t belong in mathematics: Descartes was flummoxed, too!
 |
 |
|
Statue of Pierre de Fermat by Alexandre Falguière |
Statue of Rene Descartes by Gabriel Garraud, |
As Fermat laid out his method for optimization in his earliest communication of the idea,2 it may sound like some obscure part of the US tax code that only accountants need to know, and then only for their CPA licensing exam. Fermat himself was extremely pleased with his idea,3 declaring that
We can hardly be provided with a more general method.4
Descartes initially dismissed it as nonsense. After reading copies of Fermat's work which Marin Mersenne (1588–1648) passed along to him in 1638, Descartes advised Mersenne that
If . . . he [Fermat] speaks of wanting to send you still more papers, I beg of you to ask him to think them out more carefully than those preceding.5
In the project, students are invited to decode Fermat’s method by trying it out on several of Fermat’s own examples while comparing it, step by step, to the modern method for optimization. The examples themselves are quite short, with the focus placed on understanding the method and its relation to the limit definition of the derivative rather than on attempting to solve challenging optimization problems.6 The optimization problems that Fermat used to demonstrate his method are also very geometric in nature. For instance, the last example featured in the project is the following:
Let there be a semicircle whose diameter is \(AB\); let \(DC\) be perpendicular to it. Find the maximum of the sum of the lines \(AC\) and \(CD\).7
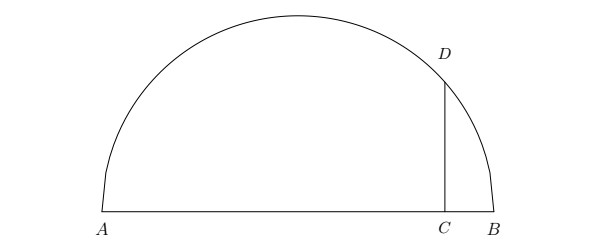
By the end of the project, the student hopefully feels as Descartes finally did when he wrote
Seeing the last method that you use for finding tangents to curved lines, I can reply to it in no other way than to say that it is very good and that, if you had explained it in this manner at the outset, I would have not contradicted it at all.8
The complete project Fermat’s Method for Finding Maxima and Minima (pdf) is ready for student use, and the LaTeX source code is available from the author by request. Instructor notes are provided to explain the purpose of the project and guide the instructor through implementation of the project.
This project is the twenty-sixth in A Series of Mini-projects from TRIUMPHS: TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources appearing in Convergence, for use in courses ranging from first-year calculus to analysis, number theory to topology, and more. Links to other mini-PSPs in the series appear below. The full TRIUMPHS collection also offers dozens of other mini-PSPs and a similar number of more extensive full-length PSPs. These include an additional twelve mini-PSPs for use in first-year calculus courses as well as four PSPs for use in a multivariable calculus course.
Notes
[1] Especially if it’s John Cleese and Michael Palin, in character!
[2] Here is how Fermat described his method in a missive that was sent to Descartes (by way of Mersennes) in January 1638 (taken from [de Fermat 1636–1642, pp. 133–134]):
Let \(a\) be the desired unknown, whether it be a length, a plane region or a solid, depending on what the given magnitude equals, and let its maximum or minimum be found in terms of \(a\), involving whatever degree. Replace this first quantity with \(a + e\), and the maximum or minimum will be found in terms of \(a\) and \(e\), with coefficients of whatever degree. These two representations of the maximum or minimum are adequated, to use Diophantus’ term, and the common terms are subtracted. Having done this, all terms from either part (affected by e or its powers) are divided each by \(e\), or by a higher power of the same, until some term of one or the other of the expressions is altogether freed from being affected by \(e\).
All terms involving \(e\) or one of its powers are then eliminated and the remaining terms are equated; or, should one of the expressions be left as nothing, then the positive terms are equated with the negatives, which reduces to the same thing. The solution to this last equation will yield the value of \(a\), which will reveal knowledge of the maximum or minimum by referring again to the earlier solutions.
[3] Of course, Fermat’s unique personal style eventually gained him a reputation for coming up with results in secret and then sending them out into the mathematical community with no indication of how one might have come upon that, almost as a puzzle for the world to solve.
[4] Excerpted from [de Fermat 1636–1642, p. 134].
[5] As quoted in [Mahoney 1994, p. 177].
[6] Should the instructor wish to take the students on a longer optimization journey, however, this project would also be the perfect launching point for a student investigation into Snell’s Law, which can be derived from Fermat’s method of optimization.
[7] Excerpted from [de Fermat 1636–1642, p. 153].
[8] As quoted in [Mahoney, 1994, p. 192].
Acknowledgments
The development of the student project Fermat’s Method for Finding Maxima and Minima has been partially supported by the TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) Project with funding from the National Science Foundation’s Improving Undergraduate STEM Education Program under Grants No. 1523494, 1523561, 1523747, 1523753, 1523898, 1524065, and 1524098. Any opinions, findings, and conclusions or recommendations expressed in this project are those of the author and do not necessarily reflect the views of the National Science Foundation.
All translations of excerpts from [de Fermat 1636–1642] in this introduction and the mini-PSP were prepared by Daniel E. Otero, Xavier University, 2022. Very minor changes were made by the author to improve readability for the student.
References
de Fermat, Pierre. 1636–1642. Methodus ad disquiredam maxima et minima (Latin). In Oeuvres de Fermat, edited by P. Tannery and C. Henry, Tome 1 (1891), 133–179. French translation in Oeuvres de Fermat, Tome 3 (1896), 121–156. Paris: Gauthier-Villars et fils.
Mahoney, Michael Sean. 1994. The Mathematical Career of Pierre de Fermat, 1601–1665: Second Edition. Princeton, NJ: Princeton University Press.
Kenneth M Monks (Front Range Community College – Boulder County Campus), "Fermat’s Method for Finding Maxima and Minima: A Mini-Primary Source Project for Calculus 1 Students," Convergence (February 2023), DOI:10.4169/convergence20230201




