- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Gerbert d'Aurillac and the March of Spain: A Convergence of Cultures - Hindu-Arabic Numerals
Gerbert also described a new system of representing numbers – a system very familiar to us today, but unknown in Western Europe at the time, where Roman numerals were still the order of the day. The new numerals, called ghobar (“dust,” from writing the numerals in the dust of a counting board) or, more generally, Hindu-Arabic, consisted of nine symbols, plus (later) a zero. Any number could be represented by placing the symbols next to each other in a particular order. The shape and orientation of the numerals evolved over the years, but at the time of Gerbert they looked something like this:
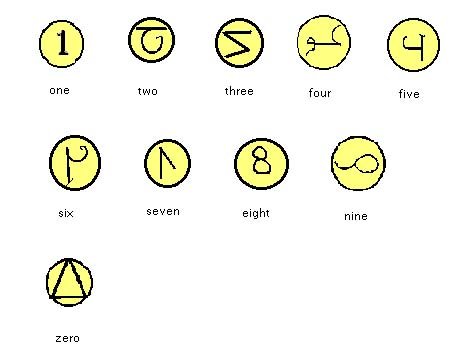
These numerals had been known in India since the sixth century C.E., and in the eighth century they began to be transmitted to Arabic scholars, who discovered how to represent decimal fractions, as well as whole numbers, with them. It wasn’t long before Arabic works describing the new system of numeration were translated into Latin; the earliest known is The Book of Addition and Subtraction according to the Hindu Calculation, by Muhammed ibn Musa al-Khwarizmi (c. 780–850). Al-Khwarizmi is probably the most famous Eastern mathematician known to students of mathematics in the West. His name gave us the term algorithm, and the word algebra first appeared in his writings. His treatise about “the Hindu calculation,” written about 820, was almost certainly available in the Spain of the tenth century.

Other scholars whose works would have been accessible to Gerbert were Abu al-Rayhan al-Biruni (973 – 1048), also from Central Asia, and Abu Sahl al-Kuhi, who lived in the second half of 10th century in Tabaristan (Persia).

There were also Jewish scholars living and working in the courts of the caliphs. Abu Sahl Dunas ibn Tamim was active in Kairouan (Tunisia) in the tenth century. Writing in Arabic in a commentary in the year 955, he mentioned an earlier work in which he described the use of Hindu numerals.
Betty Mayfield (Hood College), "Gerbert d'Aurillac and the March of Spain: A Convergence of Cultures - Hindu-Arabic Numerals," Convergence (August 2010)




