- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course

Figure 1. Ada Lovelace (1815–1852) in 1836, by Margaret Sarah Carpenter. Government Art Collection.
The name of Ada Lovelace has long been well known among mathematicians and computer scientists. Many will have seen her described as ‘the first computer programmer’—indeed, if you are old enough, you may have even encountered the programming language, Ada, that was named in her honor in 1979. Early computing pioneers acknowledged her work in the 1940s and 1950s, with Alan Turing commenting, for example, on her thoughts on artificial intelligence. Today, she is one of the few mathematical scientists who could be described as a ‘household name’ and is arguably more famous among the general public than any other female mathematician in history.
In her own lifetime she was also famous, but for a completely different reason. Augusta Ada King, Countess of Lovelace (1815–1852) was the only legitimate child of the poet Lord Byron, and, in common with the offspring of some dead celebrities today, she lived a privileged but somewhat isolated lifestyle with her every move watched and scrutinized by society. Her present-day fame stems from a 66-page paper she published in 1843, containing an account of a machine called the analytical engine [Lovelace 1843]. Designed by the famous Victorian mathematician, inventor, and polymath Charles Babbage in the 1830s, had it ever been built, this theoretical device would have been the world’s first general purpose computer—100 years before the dawn of the modern computer age.
Lovelace’s 1843 paper contained seven lengthy appendices, or ‘Notes’, with the last one, Note G, providing her chief claim to fame. In it, she outlined an iterative process by which Babbage’s machine, via a series of steps, could compute Bernoulli numbers, an irregular sequence of rational numbers, highly useful in number theory and analysis. Using the fact that these numbers are the coefficients of the \(\frac{x^n}{n!}\) terms in the infinite series expansion
\[\frac{x}{e^x-1}=\sum_{n=0}^{\infty} B_n \frac{x^n}{n!}\]
she devised an algorithm that could generate each Bernoulli number in turn. This is what has gone down in history as the world’s ‘first computer program’—although what she published was actually more akin to a modern-day execution trace than a program. (See Figure 2.)
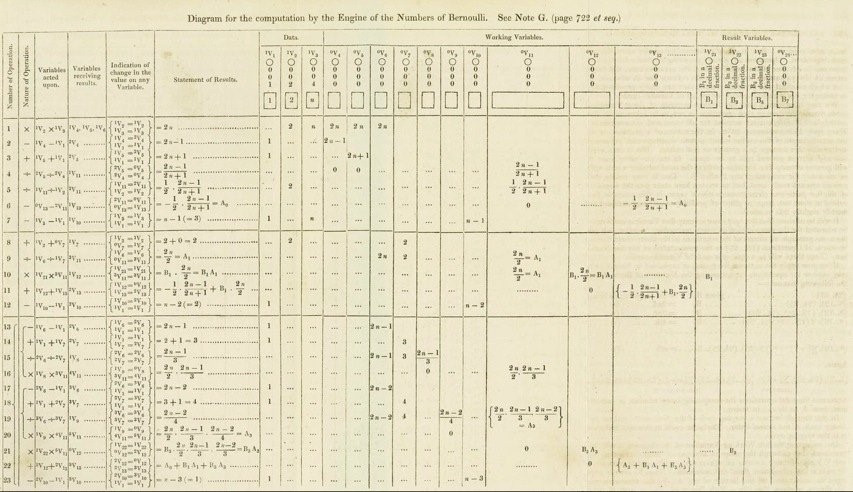
Figure 2. Diagram from Ada Lovelace’s 1843 paper showing the step-by-step procedure by which Bernoulli numbers could, in theory, be calculated by Babbage’s analytical engine [Lovelace 1843].
Over the years, the extent to which this algorithm was due to Lovelace has been hotly debated. For example, in his 1864 autobiography, Babbage noted that he had provided Lovelace with the underlying algebra for it. Nevertheless, he also recalled that she had ‘detected a grave mistake which I had made in the process’ [Babbage 1864, 136], which has led some to credit her not as the world’s first programmer, but rather as the ‘first debugger’! Originality aside, however, the fact remains that in order to explain the process of calculating Bernoulli numbers in her 1843 paper, Lovelace would have needed an understanding of the mathematics underlying the procedure. And this was by no means trivial, since the algebra involved would largely have been beyond the capability of anyone who had not had some kind of university-level tuition in mathematics. In the mid-19th century, no such education was formally available to women.
Yet it turns out that shortly before beginning work on her famous paper, Lovelace did manage to learn advanced mathematics from an unexpected source. For a period of approximately eighteen months, from the summer of 1840 to the winter of 1841/42, she took what would now be called a correspondence course with the British mathematician and logician, Augustus De Morgan (1806–1871). During this period, De Morgan introduced Lovelace to a substantial portion of what then comprised an undergraduate course in mathematics. From basic algebra and trigonometry, she progressed through logarithms and functions to the course’s principal component and the subject to which she devoted the most attention: calculus. The correspondence between Lovelace and De Morgan survives in the form of sixty-six letters from this period, now housed in the Bodleian Library in Oxford.
To shed more light on the mathematics Ada Lovelace actually studied in order to produce her famous paper of 1843, a recent research project, undertaken by Chris Hollings, Ursula Martin and myself, looked in detail at these surviving letters. Our research resulted in two papers, [Hollings et al. 2017a] and [Hollings et al. 2017b], and an expository book [Hollings, et al. 2018], differing from previous studies in concentrating specifically on the details of the actual mathematics that Lovelace studied with De Morgan. We found that she was an extremely keen and capable student, although certainly prone to the usual beginner’s mistakes and misapprehensions. Not surprisingly, these errors featured prominently in her letters to De Morgan, since she would not have wasted time (and paper) telling him what she already understood, but would naturally have written more to ask questions about material on which she needed further explanation and help.
It is these misunderstandings as highlighted by Lovelace in her correspondence with De Morgan that form the basis of this article. I have selected ten particular problems (homework exercises, if you like) on which Lovelace encountered difficulties at some point in her course of study; they mainly concern calculus, although some are more foundational, involving limits or basic algebra. As we will see, some of these problems appear almost trivial, while others are more sophisticated. But they all underscore common sources of confusion that still plague mathematics students and their teachers today. For this reason, they provide excellent templates for exercises that may be used in the classroom by students and teachers alike. Regardless of the level of the reader’s mathematical expertise, what emerges irrefutably from looking at all of these problems, together with Lovelace’s flawed attempts to solve them, is the comforting notion that even the most famous mathematicians make mistakes.
Adrian Rice (Randolph-Macon College), "Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course," Convergence (September 2021), DOI:10.4169/convergence20210904




