- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 10
Our final problem comes close to the end of Lovelace’s correspondence course with De Morgan. By early November 1841, she had progressed to the subject of second-order differential equations. One of the examples with which she had trouble was on page 156 of De Morgan’s Calculus. Given the nonhomogeneous equation
\[\frac{d^2 u}{d\theta^2 }+u=\cos\theta\]
De Morgan gave its general solution as
\[u=C \sin \theta + C' \cos \theta + \sin\theta \int cos^2 \theta d \theta - \frac{1}{2} \cos \theta \int \sin 2\theta d\theta,\] which, since
\[ \int \cos^2 \theta d\theta = \frac{1}{2} \theta + \frac{1}{4} \sin 2 \theta \, \, \mbox{ and } \,\, \int \sin 2\theta d\theta = -\frac{1}{2} \cos 2\theta \] resulted in
\[u=C \sin\theta + C' \cos \theta +\frac{1}{2}\theta \sin \theta + \frac{1}{4} \sin 2 \theta \sin \theta+ \frac{1}{4} \cos\theta \cos 2\theta.\] Using double angle formulae, he converted this into
\[u=C \sin \theta + C' \cos \theta + \frac{1}{2}\theta \sin \theta+ \frac{1}{4} \cos \theta,\] which he then expressed in its final form as
\[u=C \sin \theta+C' \cos \theta + \frac{1}{2} \sin \theta,\] along with a challenge: ‘Explain this step?’ (See Figure 12).
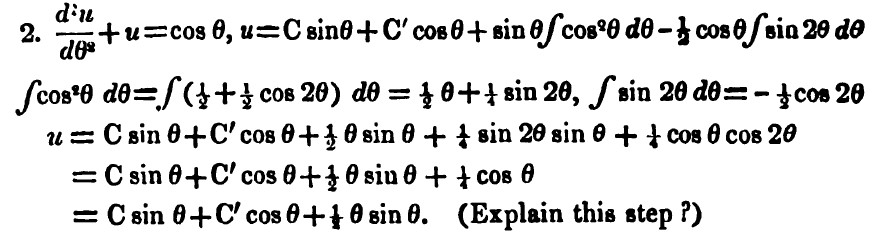
Figure 12. Problem from page 156 of De Morgan’s Differential and Integral Calculus.
The trouble was, as Lovelace remarked in a letter to De Morgan, ‘I cannot “explain this step”.’ She noted that ‘in the previous line, we have: \[\begin{array}{r} (1) \ldots u = C \sin \theta +C' \cos \theta + \frac{1}{2}\theta \sin \theta + \frac{1}{4} \cos \theta \mbox{ (quite clear)} \end{array}\] \[\begin{array}{rcl} (2) \ldots \mbox{ And } u &=&\cos \theta -\frac{d^2 u}{d \theta ^2 } \mbox{ (by hypothesis)} \\ &=& \frac{1}{4} \cos \theta+\left (\frac{3}{4} \cos \theta-\frac{d^2 u}{d\theta^2} \right ) \end{array}\]
whence one may conclude that \[C \sin\theta+C' \cos \theta + \frac{1}{2}\theta\sin \theta=\frac{3}{4}\cos \theta-\frac{d^2 u}{d\theta^2} \] But how \(u=C \sin \theta+C' \cos \theta+\sin\theta\cdot\frac{1}{2} \theta\) is to be deduced I do not discover.’ [LB 170, 4 Nov. [1841], ff. 132v-133r]
Not deterred, she tried again:
By subtracting \(\frac{1}{4}\cos \theta\) from both sides of (1), we get \[u-\frac{1}{4} \cos \theta= C \sin \theta+C' \cos \theta+ \frac{1}{2} \theta \sin \theta\] But unless \(\frac{1}{4} \cos \theta=0\), (which would only be the case I conceive if \(\theta=\pi/2\)), I do not see how to derive the equation \(\ldots\) [LB 170, 4 Nov. [1841], f. 133r].
De Morgan’s final solution is certainly correct. So can you explain why the \(\frac{1}{4} \cos \theta\) mysteriously disappears?
Return to Main Problems Page.
Continue to Main Solutions Page.
Adrian Rice (Randolph-Macon College), "Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 10," Convergence (September 2021)




