- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
How to Calculate \(\pi\): Buffon's Needle – A Mini-Primary Source Project on Geometric Probability for Calculus 2 Students, Pre-service Teachers and Others
Readers of Convergence are likely to know several ways to calculate \(\pi\). One method—as interesting as it is impractical—can be traced to a 1777 essay by Georges-Louis LeClerc, the Comte de Buffon (1707–1788). The basic idea comes from a question of probability: if a needle of length l is thrown randomly onto a floor marked with parallel lines, set at distance d apart, what is the probability that the needle will cross one of the lines? The lovely answer, calculated by Buffon, is that the probability is precisely \(\frac{1}{\pi}\). While Buffon’s goal was not to calculate \(\pi\), at least one scholar later claimed to have tried to estimate its value using this method. In the mini-Primary Source Project (mini-PSP) How to Calculate \(\pi\): Buffon’s Needle, students examine that claim after first exploring the key ideas from Buffon’s original essay.
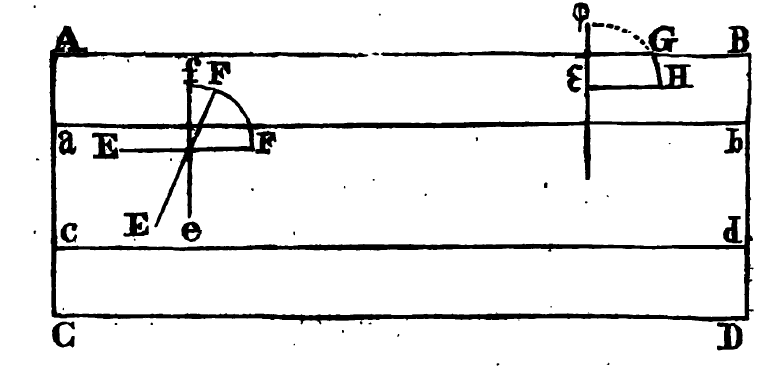
Buffon’s sketch of the Needle Problem.
Beginning shortly before 1750, and continuing until his death in 1788, Buffon published a multi-volume opus, the Histoire Naturelle, which attempted to describe all of nature. To the fourth volume of this work, Discours sur la nature des Animaux, Les Animaux domestiques (Discourse on the nature of Animals: domestic Animals), was appended a “Supplement.” The contents of the supplement give a view into the wide-ranging mind of this natural historian. It contains actuarial tables; additions to already-published articles on childbirth, puberty, the sense of hearing (and many others); replies to scholars who had commented on earlier volumes; and more. Tucked into the middle of all these was a curious work called Essais d’Arithmetique morale (Essays on moral arithmetic) [Buffon 1777].
In a marvelous example of the microcosm reflecting the macrocosm, the Essais has a structure every bit as labyrinthine and fractaline as the larger publication that contains it. In it, Buffon used arguments from what is now known as Utility Theory to argue against gambling; introduced the “Saint Petersburg game” to France; and sought out probabilistic bounds on what it means to be “certain” that an event will occur. Then, just before a philosophical conclusion, he introduced the idea of geometric probability. Although he did not use the term itself, it conveys well his idea that he could ask probabilistic questions that are to be answered geometrically.
Buffon began with the question: If we throw a coin on a floor paved with equal square tiles, and bet as to whether it will fall across a line between two tiles, what size should the tiles be in order for the game to be fair? He concluded that the ratio of the border length to the diameter of the coin should be \(1: 1 - \sqrt\frac{1}{2}\). He then asked the same question for tiles in the form of equilateral triangles, diamonds, and hexagons—stopping when he had exhausted the set of symmetric plane-filling shapes. Next, he made further calculations for each of these shapes, asking about the probability the coin would fall crossing two lines.
Finally, he turned to the question of throwing not a coin, but something one-dimensional (a “needle” or a “baguette”). He replaced the tiles on the floor with parallel lines, and ended up tackling what we now know as “Buffon’s Needle Problem.” Buffon pointed out that in this case, the lack of symmetry meant the problem “would demand a little more geometry.” While he avoided any description of his calculations for the cases described above, he gave enough detail of the needle calculation that the modern reader can follow his work. At the same time, his details are sparse enough—and foreign enough to the modern eye—to necessitate a close and careful read.
This careful read, and an invitation to check details and read between the lines, is the driving force behind the Primary Source Project (PSP) How to Calculate \(\pi\): Buffon’s Needle. Unusually, this project comes in two versions: one suitable for students with no calculus background (but a bit of trigonometry) and one for students who have learned some basic integration. It turns out that most of the creative and clever parts of the geometric probability argument Buffon gave concern carefully setting up the problem, with calculus playing only a minor (if vital) role. Thus calculus students can have the satisfaction of working through the entire argument, which involves evaluating an integral of a trigonometric function using integration by parts. In the non-calculus version, students instead complete Buffon’s argument by looking at the area under a cosine curve, and they are presented with the area value needed to allow them to work through all other details of the mathematics of the problem. Both versions require students to be able to draw a right triangle, label the edges and angles, and write an expression relating some of these using cosine.
The final section of the PSP concerns the famous experiment of Mario Lazzarini, who reported in 1901 that he had conducted an experiment using a floor ruled with parallel lines, and a large set of needles with length equal to \(\frac{5}{6}\) the distance between them [Lazzarini 1901]. He claimed to have thrown these needles on the floor an impressive 3408 times, and he used the number of needles crossing a line to “reverse-engineer” Buffon’s calculations to calculate the value of \(\pi\) based on the experiment. His answer matched the true value to an impressive six decimal places—a feat that seems to have brought Buffon’s Needle Problem out from the obscure text-within-a-text in which it lay to the attention of the wider world. Indeed, a Google Ngrams search of the frequency of occurrence of the phrase “Buffon’s needle” shows a dramatic rise in its use in English-language books starting soon after Lazzarini’s announcement—a rise that shows no evidence of abating (see the graph below). At the same time, his experiment has been viewed with suspicion by later generations, and in the last part of the PSP, students have a chance to engage these suspicions directly.
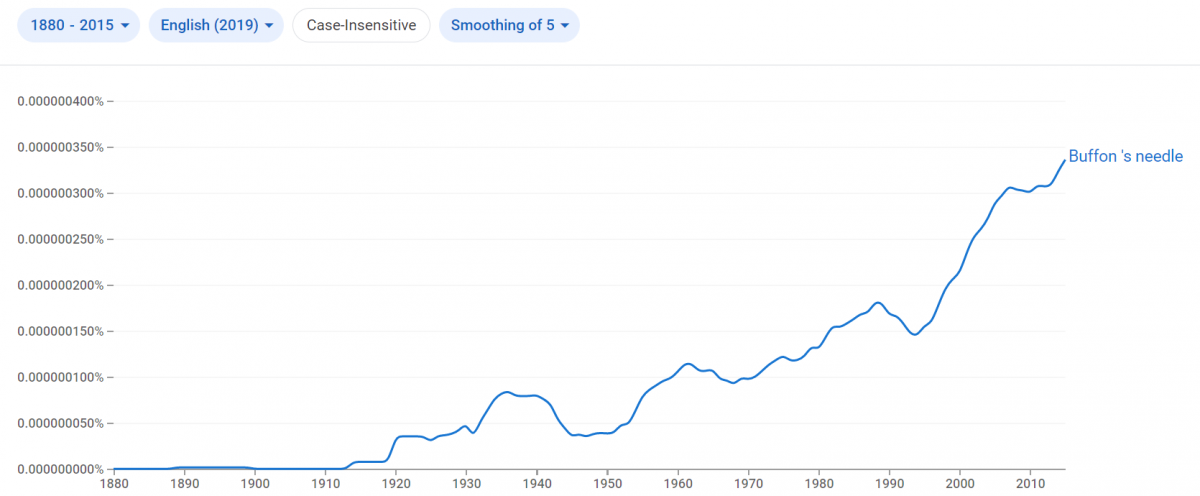
Frequency of occurrence of the phrase “Buffon’s needle” in English language books between 1800 and 2015 (phrase search as case-insensitive, graphs smoothed with a five-year moving average), as provided by Google Ngram Viewer. The growth rate is roughly exponential, with the relative frequency of the phrase in printed English-language books doubling roughly every 30 years since the early 20th century. If left unchecked, the English language will consist of nothing but the words “Buffon’s needle” repeated endlessly by about 2650 CE.
Both versions of the project are ready for student use.
- How to Calculate \(\pi\): Buffon's Needle – Non-calculus version (pdf file)
- How to Calculate \(\pi\): Buffon's Needle – Calculus version (pdf file)
A set of instructor notes that explains the purpose of the project and offers practical advice for classroom use is appended at the end of each project. The LaTeX source code of each project is also available from the author by request.
This project is the twenty-third in A Series of Mini-projects from TRIUMPHS: TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources appearing in Convergence, which includes a second mini-PSP related to the calculation of \(\pi\):
Links to all mini-PSPs in the series are given below. The full TRIUMPHS collection offers dozens of other mini-PSPs and a similar number of more extensive full-length PSPs, for use in courses ranging from first year calculus to analysis, number theory to topology, and more.
Acknowledgments
The development of the student projects presented in this article has been partially supported by the TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) project with funding from the National Science Foundation’s Improving Undergraduate STEM Education Program under Grants No. 1523494, 1523561, 1523747, 1523753, 1523898, 1524065, and 1524098. Any opinions, findings, and conclusions or recommendations expressed in this project are those of the author and do not necessarily reflect the views of the National Science Foundation.
References
Buffon, Comte de (Georges-Louis LeClerc). 1777. Essai d’Arithmétique morale, Supplément à l’Histoire Naturelle, volume 4. Paris: H. Champion.
Lazzarini, Mario. 1901. Un’applicazione del calcolo della probabilita alla ricerca esperimentale di un valore approssimato di \(\pi\). Periodico di Matematica per l'Insegnamento Secondario 4:140–143.
Dominic Klyve (Central Washington University), "How to Calculate \(\pi\): Buffon's Needle – A Mini-Primary Source Project on Geometric Probability for Calculus 2 Students, Pre-service Teachers and Others," Convergence (May 2022), DOI:10.4169/convergence20220501




