- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Impacts of a Unique Course on the History of Mathematics in the Islamic World - Some Pedagogical Aspects
Anyone who studies the history of mathematics realizes that the way we teach mathematics is often misleading. Historically, new mathematical material is rarely discovered in the way it is presented in textbooks. When the teachers do not know about the history of the material well enough to explain the way mathematics was originally developed (when the details of the historical development are known, which is not always the case), some valuable pedagogical dimensions are lost. I would like to give a few examples that show the disconnect between historical development and teaching practice.
Today, when they hear the term algebra, most students probably think of symbols (such as x, y, and z) and their manipulations. However, for many centuries algebra was done completely in prose (except that sometimes geometry and geometric figures were used to explain or justify algebraic procedures). The introduction of symbolism into algebra is a much later phenomenon ([8], [28], [12]). Hence symbol manipulation is not the essence of algebra. As teachers of mathematics we need to better explain what the main idea is in algebra. As Al-Samawʾal explicitly stated and Omar Khayyám further explained, algebra is operating on the unknown quantities in the same way you operate on the known quantities, and using the relations between the known and the unknown quantities to determine the unknown quantities. Knowing the historical development is relevant and helpful.
The method of “completing the square” is a standard one in the modern school curriculum. We often teach it as a purely algebraic procedure to manipulate and solve quadratic expressions or equations (by extension, possibly higher degree expressions as well). Historically, however, it was based on the geometry of squares, rectangles, and L-shaped figures formed from them, which together represented quadratic expressions and equations. In the example below, we'll show how Thābit ibn Qurra (836-901) used a geometry theorem stating that an L-shaped geometric figure has the same area as a square to transform a quadratic equation we would write as \(x^2 + m = nx\) into the form \[m+\left(x-\frac{n}{2}\right)^2 = \left(\dfrac{n}{2}\right)^2,\] thereby making it easier to solve. Since the general idea of this method was to replace L-shaped figures by squares, perhaps it would be more accurate to call the method "converting to the square."
Early Islamic scholars, who were pioneers of algebra, used the idea of "completing the square" or "converting to the square" to justify their procedures to solve quadratic equations. Rigorously established geometry theorems from Euclid's Elements formed a solid foundation for their approach. For example, Thābit ibn Qurra’s use of Propositions 5 and 6 from Book II of the Elements in justifying solutions to quadratic equations is described in Berggren's text ([2], pages 104-107). It is unfortunate that many teachers and students miss out on this connection between geometry and algebra that was historically well established.
Euclid's Elements, Book II, Proposition 5. If a line AE is divided at B and bisected at W, then the rectangle AB x BE plus the square on BW is equal to the square on AW.
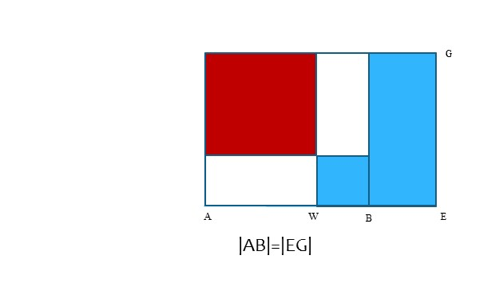
Figure 2. The diagram above illustrates Proposition 5 of Euclid's Elements. Under the given hypotheses, the area of the L-shaped blue region is equal to the area of the red square.
For more details on Euclid's Elements, Book II, Proposition 5 and Proposition 6, see David Joyce's presentation of the text at his website: http://aleph0.clarku.edu/~djoyce/java/elements/.
Ibn Qurra used Proposition 5 to solve one type of Al-Khwārizmī’s quadratic equations; namely, the quadratic equation that we would write as \(x^2 + m = nx,\) where \(x,\) \(m,\) and \(n\) are positive.

Figure 3. The diagram above illustrates the application of Proposition 5 to the solution for \(x\) of the quadratic equation \(x^2 + m = nx,\) where \(x,\) \(m,\) and \(n\) are positive. By Proposition 5, m + |BW|2 = |AW|2. Since |AW| and m are known, |BW| can be found. Since |BW| = \(x - \dfrac{n}{2}\) and \(n\) is known, \(x\) can be found. Or, in more modern terms, the area equation, m + |BW|2 = |AW|2, can be written algebraically as \[m+\left(x-\frac{n}{2}\right)^2= \left(\frac{n}{2}\right)^2,\] and solved for \(x.\)
In the quadratic equation \(x^2+m=nx,\) \(m\) and \(n\) are known, positive quantities. In the figure above, the area of the rectangle GB is \(m.\) One side of the largest rectangle is of length \(n\) (hence known), the other side is of length \(x\) (hence unknown). The length of segment AB is also \(x,\) where \(n> x\) and, in this case, \(x> \dfrac{n}{2}.\) Therefore, the figure represents the equation \(x^2+m=nx\) (since each side of the equation is the area of the largest rectangle).
Now we apply Proposition 5. First note that since \(n\) is known and W is the midpoint of segment AE, the length of segment AW is known to be \(\dfrac{n}{2}.\) Consider the L-shaped blue region. Its area is \[m+\left(x-\frac{n}{2}\right)^2.\] By Proposition 5, its area is also equal to \(\left(\dfrac{n}{2}\right)^2.\) Thus, we obtain the equation \[m+\left(x-\frac{n}{2}\right)^2 = \left(\dfrac{n}{2}\right)^2.\] Therefore, the original equation \(x^2+m=nx\) is transformed to \[m+\left(x-\frac{n}{2}\right)^2= \left(\frac{n}{2}\right)^2\] by Proposition 5. This is precisely what we get when we “complete the square” in the equation \(x^2+m=nx\) in a purely symbolic way.

Figure 4. The page above is from a manuscript copy of Al-Khwārizmī's Al-Jabr. For details of how the square is completed by filling in its four corners, see "Mathematical Treasures - Al-Khwarizmi's Algebra" here in Convergence. (Source: Columbia University Libraries)
Today, algebra is arguably the most important branch of modern mathematics as evidenced by the fact that one can take almost any subfield of modern mathematics and stick the adjective "algebra" in front of it and there turns out to be such a discipline; for example, algebraic geometry, algebraic number theory, algebraic topology, algebraic coding theory, algebraic combinatorics, and many others. It is really interesting to trace the origins of the point of view that made algebra such a powerful tool in modern mathematics. When we study the works of Omar Khayyám (1048-1131), one of the great mathematicians of medieval Islam who is better known as a poet, we find some hints. Al-Khwārizmī (780-850), an earlier and possibly better known Islamic mathematician, wrote the first known algebra book in history, copies of which survive (see Notes 1 and 2). From the title of this book, we get the English word algebra as a transliteration of the Arabic “al-jabr” ( الجبر ) [19], and Al-Khwārizmī's own name became the term algorithm over the ages. While Al-Khwārizmī classified and solved quadratic equations in a systematic way, Omar Khayyám did the same for cubic equations. One major difference between the works of the two scholars was the following: al-Khwārizmī studied quadratic equations systematically and presented numerical recipes (“algorithms”) to solve them, whereas Khayyám could only solve cubic equations in purely geometric ways. That is, his solution to a particular problem would be a geometric quantity such as the length of a line segment obtained after a sequence of geometric constructions, some involving only Euclidean tools and others requiring conic sections. Khayyám acknowledged that he failed to find numerical solutions to cubic equations like Al-Khwārizmī did for quadratic equations, and he hoped that mathematicians after him would succeed in doing so. Indeed, his wish was fulfilled some four centuries later. Despite this shortcoming, his view of algebra was remarkably similar to the modern view. We can see that his work contained the seed of the huge tree that we have in modern mathematics when we read his words (quote from [2], pages 123-124):
Algebra. By the help of God and with his precious assistance I say that algebra is a scientific art. The objects with which it deals are absolute numbers and (geometrical) magnitudes which, though themselves unknown, are related to things which are known, whereby the determination of the unknown quantities is possible … What one searches for in the algebraic art are the relations that lead from the known to the unknown, to discover which is the object of algebra …
As Berggren pointed out, if these relations happen to come from geometry, the problem is no less algebraic in Khayyám’s view. The main idea of algebra, according to Khayyám, is to use relationships between known and unknown quantities to figure out the unknown(s). It does not matter where those quantities come from. They need not be numbers or numerical values. Today, we can appreciate the value of Khayyám’s work and his point of view in a deeper way.
A recent article in Convergence, "A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation" [14], illustrates Khayyám’s method of solution to cubic equations using GeoGebra and provides more information about his work and the history of cubic equations.
 |
 |
Figure 5. Left: Muhammed ibn Musa al-Khwārizmī (circa 780-850) was the author of the earliest known book in history in which the term algebra was used as a technical mathematical term. Moreover, his name is the source of the term algorithm, a fundamental notion in modern computing. His contributions to astronomy were acknowledged by the naming of a crater on the moon after him. (Source: Wikimedia Commons)
Right: Statue of Omar Khayyám (1048-1131) in Nishapur, Iran (photographed by Muhammad Mahdi Karim, December 2011. Source: Wikimedia Commons, licensed under GFDL 1.2)
I recently realized from a computer programming textbook ([23], page 14) that the term algorithm had a much narrower meaning historically than it does today, referring originally to procedures to solve algebraic or numerical equations. (Incidentally, I had been teaching computer programming using [23] as a textbook for many years before I began teaching the History of Mathematics in the Islamic World course, but the note there did not capture my attention before.) As noted above, the term algorithm comes from Al-Khwārizmī’s own name and the term algebra from the title of Al-Khwārizmī’s algebra text. Thus, two fundamental terms of modern science come from the same source. Al-Khwārizmī gave recipes, or procedures, to solve quadratic equations in [19], effectively the quadratic formula but entirely in words. Hence, one might be tempted to conclude that his algebra text was the reason why both terms came from the same scholar. But it turns out that it is his work in another area that explains why the term algorithm is associated to his name. Al-Khwārizmī wrote one of the earlier books in the Islamic civilization that introduced the decimal system from India. The original Arabic text is lost but a Latin translation is extant. The first word of the title of the Latin translation of that book, Algoritmi de numero Indorum (Al-Khwārizmī on the Indian Numbers), gave rise to the word algorithm ([16], where the authors translate the title as Al-Khwarizmi on the Hindu Art of Reckoning). Unfortunately, many students and teachers are not aware of these connections.
Note 1. We are fortunate to have copies of Al-Khwārizmī’s original text in algebra in Arabic, which has been translated to English. Unfortunately, a great many historical scientific books are lost.
Note 2. There were certainly works in earlier civilizations that can be considered as algebra, but scholar of Islamic mathematics Roshdi Rashed classified Al-Khwārizmī’s book as “a foundation text for algebra, since it is the work in which algebra was, for the first time in history, conceived as a mathematical discipline independent of geometry and of arithmetic” [19].
Nuh Aydin (Kenyon College), "Impacts of a Unique Course on the History of Mathematics in the Islamic World - Some Pedagogical Aspects," Convergence (July 2017)




