- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mabel Sykes: A Life Untold and an Architectural Geometry Book Rediscovered – The Source Book
Now let’s take a closer look at Sykes’ A Source Book of Problems for Geometry Based upon Industrial Design and Architectural Ornament. In his review of the book, H. E. Cobb wrote, “The present volume is a welcome contribution to the endeavor to make the mathematical work in our schools more practical and tangible” [51]. In her preface Sykes began,
The author is fully aware of the danger involved in offering this book to teachers of geometry. At present there is a widespread tendency in education to substitute amusement for downright work. This temptation presents itself in varied and subtle forms to all teachers. ... A design which is not an easily recognized application of a known construction is certainly of doubtful value. ... But geometry gives, as no other subject can give, an appreciation of form as it exists in the material world, and of the dependence of one form upon another [40].
Sykes’ initial warning aside, we have found this book to be a great resource for exploring geometric constructions used in architectural designs. In over 1800 exercises, Sykes analyzed geometric patterns found in architectural elements from tilings to windows and arches. Each of the six chapters is devoted to a particular form or design. Buildings from across the globe provide examples of wall tilings, mosaics, parquet floors, stained glass, ironwork, trusses and arches. Two of the chapters are devoted to Gothic tracery, a term originally used to describe the elaborate stonework that supports the glass within a window opening. It has come to include designs found in similar architectural features cut or cast from stone, or carved in wood, such as open screens, parapets, and balustrades. Sykes also included examples of geometric design found in jewelry and needlework. Hundreds of beautiful diagrams of tilings, tracery, and arches are presented, often alongside an illustration of the building that inspired the problem. There are Roman and Byzantine mosaics, Moorish and Greek tilings, Gothic and Persian arches, and Arabic and Egyptian parquet floor designs. In her historical comments, Sykes noted the interconnectedness and ubiquitousness of designs that span millennia, continents, and cultures. For example, the quadrifoil, while found in medieval Gothic designs, can also be seen in Chinese, Japanese and Native American decoration [40]. Here, we highlight five designs from Sykes’ book.
Figure 6: Parquet Flooring.
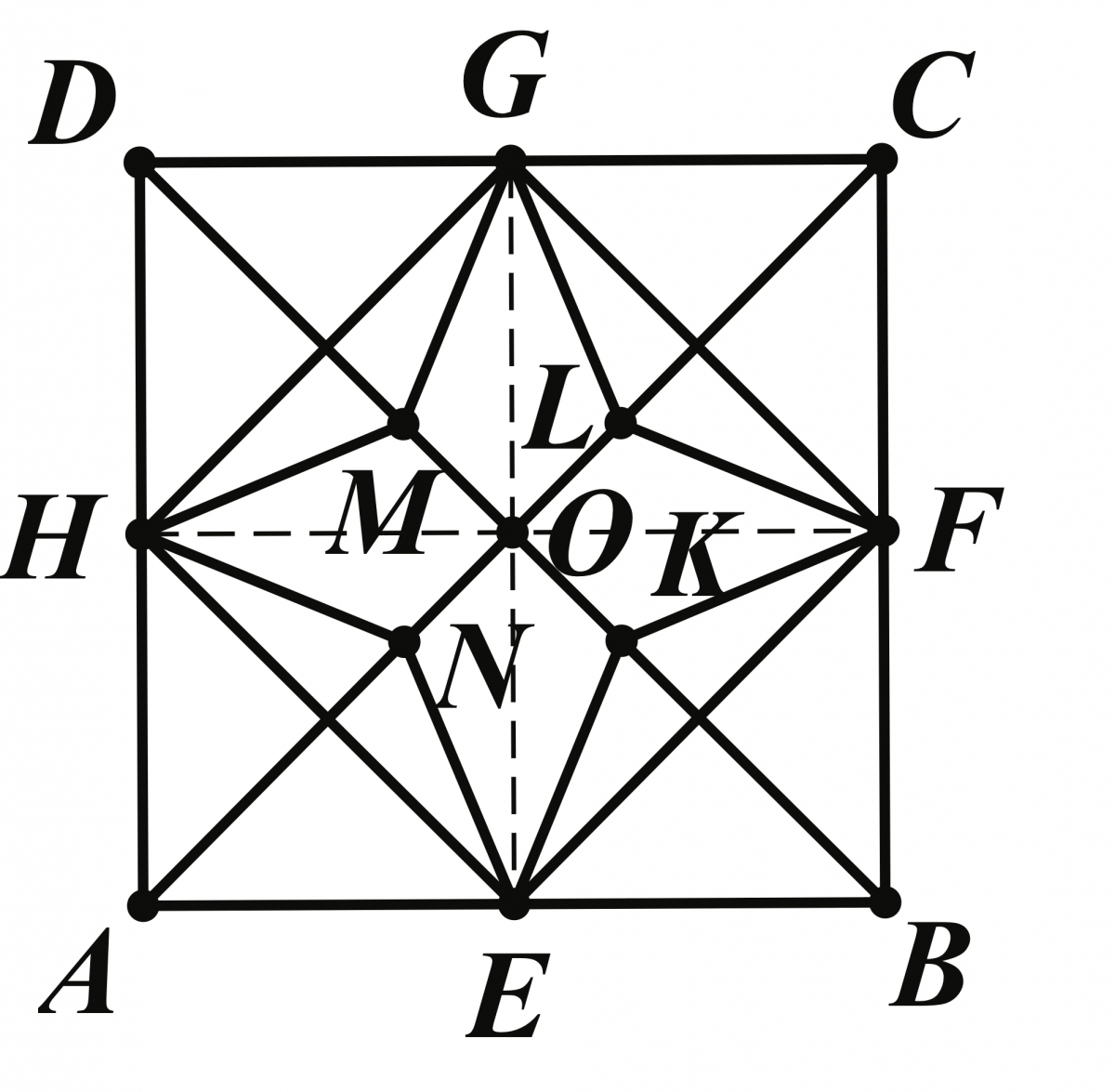
From page 59 of the Parquet Floor Designs chapter we have the example illustrated in Figure 6. This figure is a \(2 \times 2\) array of the individual tile shown in Figure 7. Sykes describes a single tile as follows: “\(ABCD\) is a square with diameters and diagonals. \(OK = OL = OM = ON\) and the points are joined as shown.” While use of the term diameter for a square is a bit unusual, in this case we take it to mean the segments joining the midpoints of opposite sides. The accompanying exercises include the following:
- Prove that:
- \(EK = KF = FL\), etc.;
- \(\angle MHN = \angle NEK = \angle KFL\), etc.;
- \(ONEK\) and \(OKFL\) are congruent.
- If \(AB = 12\) and \(OK = 3\), find the area of the star \(EKFLG\) etc.
- If \(OK =\frac{OB}{n}\), compare the areas of \(\triangle EKO\) and \(\triangle EBO\), and prove that the area of the star is \(\frac{1}{n}\) that of the square \(ABCD\).
Figure 7: Individual Tile for Parquet Flooring.
A total of eleven exercises are associated with this tile design. Notice that the length of OK is not prescribed and can be any positive value that is less than half of \(OB\). As a special case, Sykes considers when EK, KF, FL, etc. bisect the angles \(\angle OEF\), \(\angle OFE\), \(\angle OFG\), etc., respectively. As shown in the exercises below, this choice then determines the length of \(OK\). (This is, in fact, the case we have illustrated in Figure 7.) Sykes gave additional exercises for this case as given below. Here, the suggestions and answers are also provided by Sykes.
- Prove that \(EK\), \(KF\), and \(OB\) are concurrent. Suggestion: The bisectors of the angles of a triangle are concurrent.
- If \(AB = a\), find
- the length of \(OK\) \(\left (\frac{a}{2}(\sqrt{2}-1)\right) \);
- the area of \(EKFLG\) etc. \(\left ( \frac{a^2}{2}(2-\sqrt{2})\right) \);
- and of \(EKFB\) \(\left (\frac{a^2}{8}\sqrt{2}\right )\);.
Our next three examples are also designs based on a square and are found in three different sections of Chapter III. We have included interactive GeoGebra applets for each.
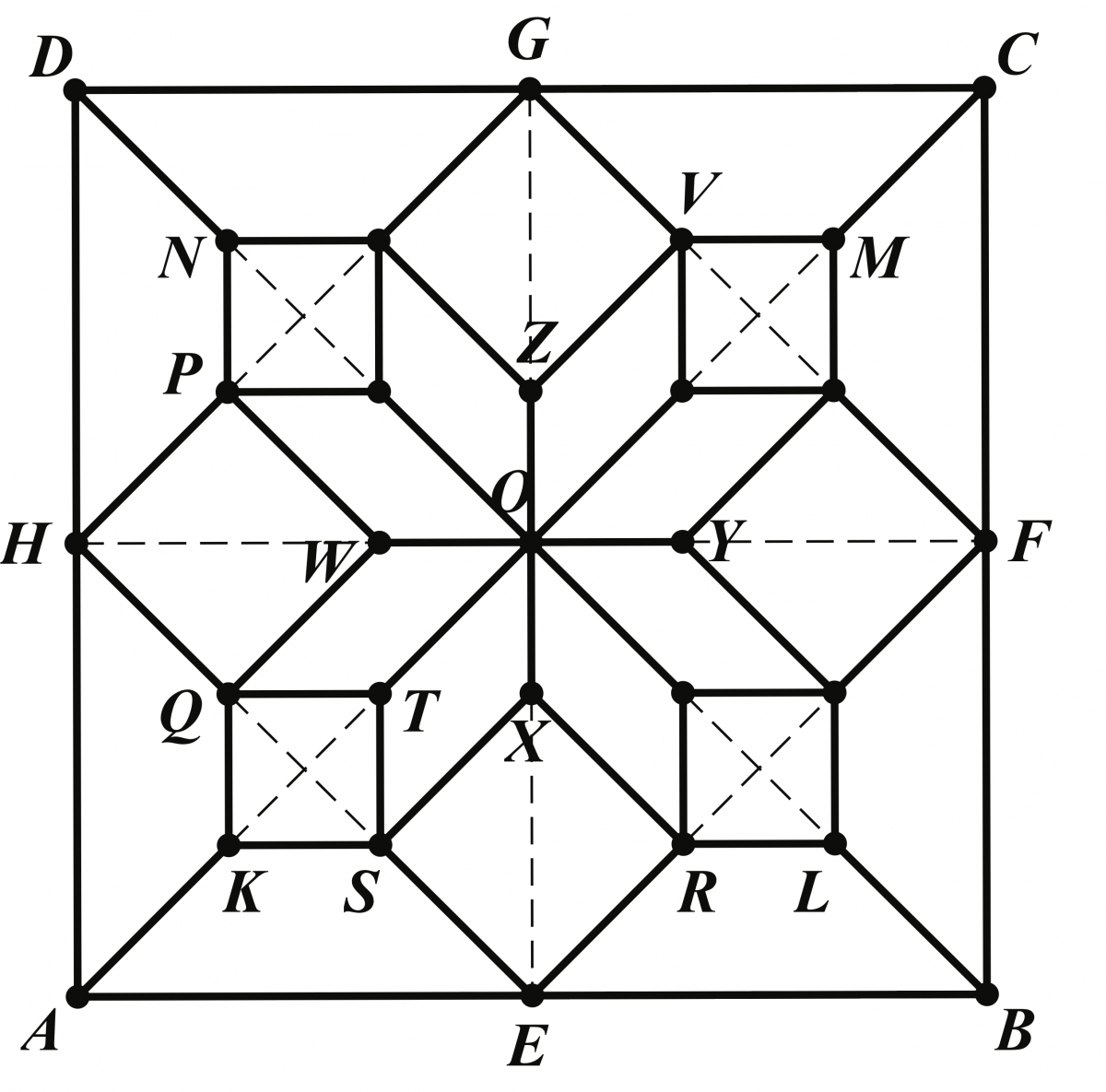
The first of these, shown in Figure 8, is one tile of a linoleum design found on page 75 in the section Designs based on octagons within squares. For this tile Sykes wrote “\(ABCD\) is a square, \(AR = VB = BU\), etc., and the points are joined as indicated.” Here, length \(AR\) is allowed to vary, as demonstrated by the GeoGebra applet found in Figure 9. Many of the exercises are focused on the special case when octagon \(EFGHKLMN\) (in Figure 8) is regular.
Figure 8: Linoleum Design.
Figure 9: Applet for design from Figure 8.
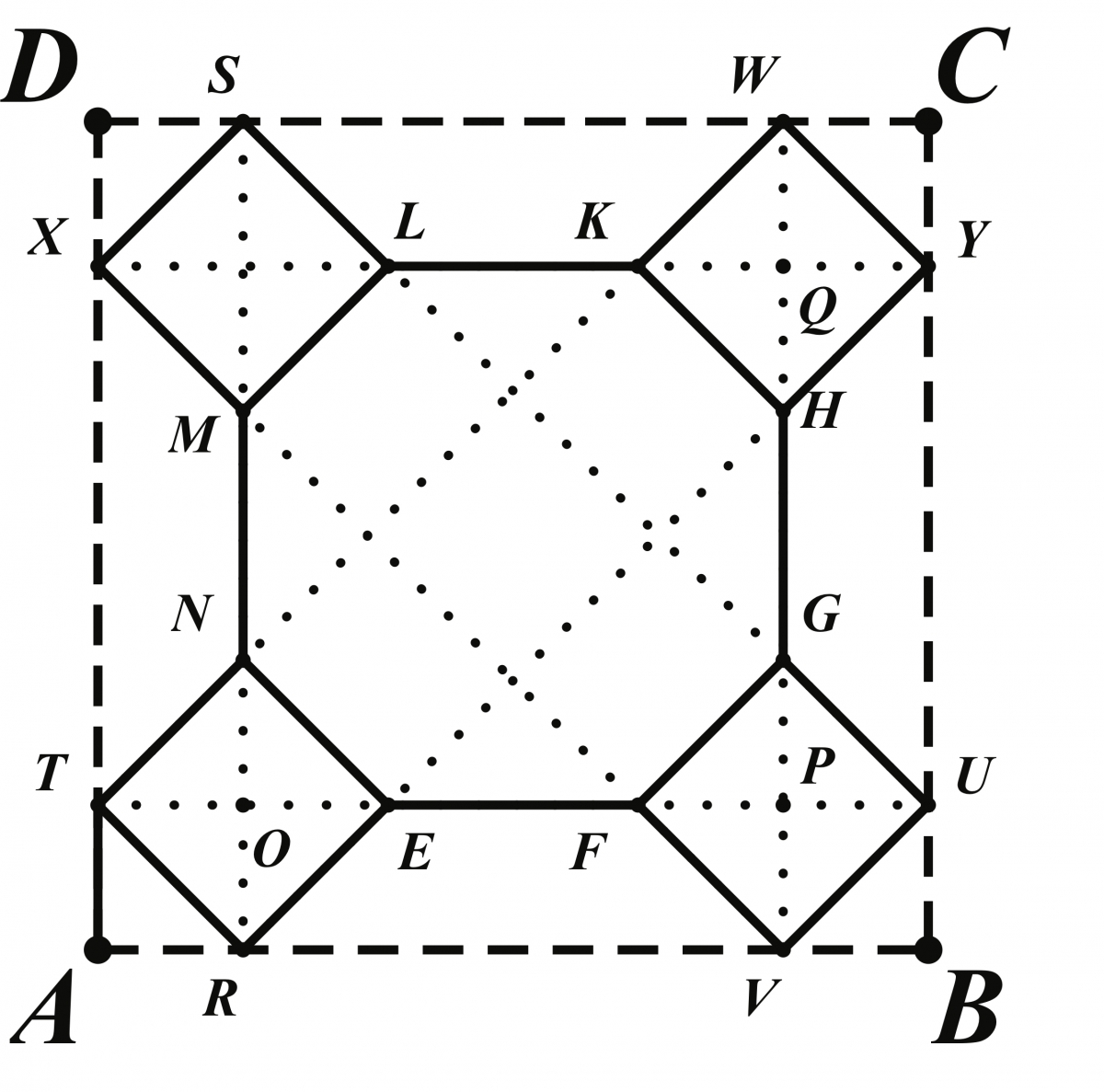
Our third example from the Source Book is another parquet floor tile, as illustrated in Figure 10, and comes from page 92 in the section Designs containing eight-pointed stars. For this figure, Sykes described: “\(ABCD\) is a square. \(E\), \(F\), \(G\), and \(H\) are the middle points of the sides. \(OK = OL = OM = ON\). The squares \(EFGH\)and \(KLMN\) are drawn. Points \(Q\) and \(V\), \(P\) and \(R\), etc., also \(K\) and \(L\), \(V\)and \(R\), \(K\) and \(N\), etc., are joined. Here, length \(AK\)may be any positive value less than half of \(AO\), as demonstrated by the GeoGebra found in Figure 11.
Figure 10: Parquet Flooring.
Figure 11: Applet for design from Figure 10.
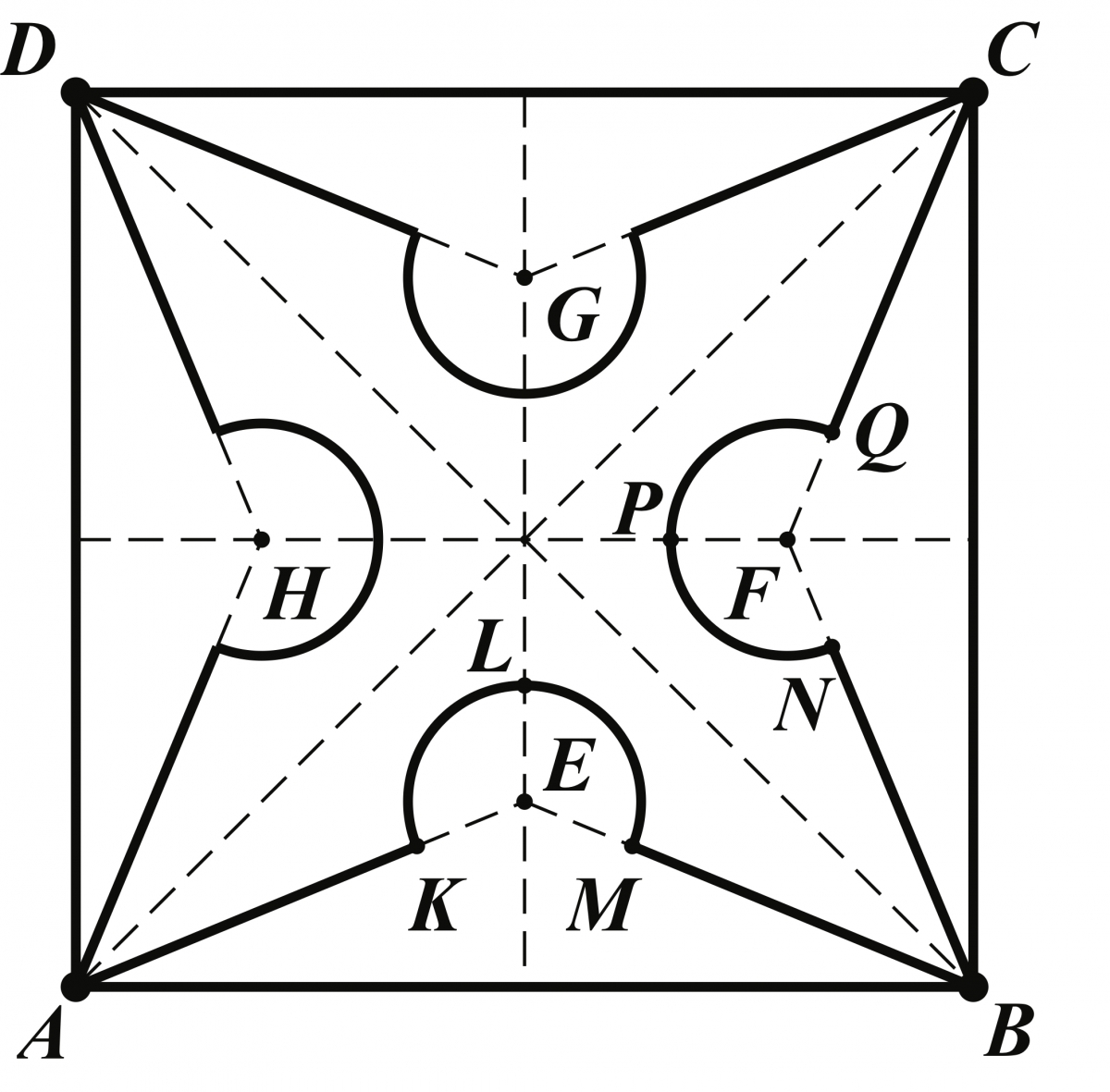
Our fourth example, as illustrated in Figure 12, is a tile design from a counter railing that can be found on page 125 in the section Designs formed from line-segments and circle-arcs. Here, Sykes explained “\(ABCD\) is a square with diameters \(EG\) and \(FH\) and diagonals \(AC\) and \(BD\). \(KE = EM = FN = FQ\), etc.; and \(\angle EAB =\angle EBA = \angle FBC = \) \(\angle FCB = \angle GCD\), etc.” There are two choices for this design. The angle \(\angle EAB \) may be any positive angle less than \(45^o\). In Figure 12 we have chosen to bisect \(\angle CAB\). Furthermore, length \(AK\) may vary, as demonstrated by the GeoGebra applet in Figure 13. Like the exercises from our first tile design example, the associated exercises for the previous three examples also include length and area determinations for specific cases of the design.
Figure 12: Tile for counter railing design.
Figure 13: Applet for design from Figure 12.
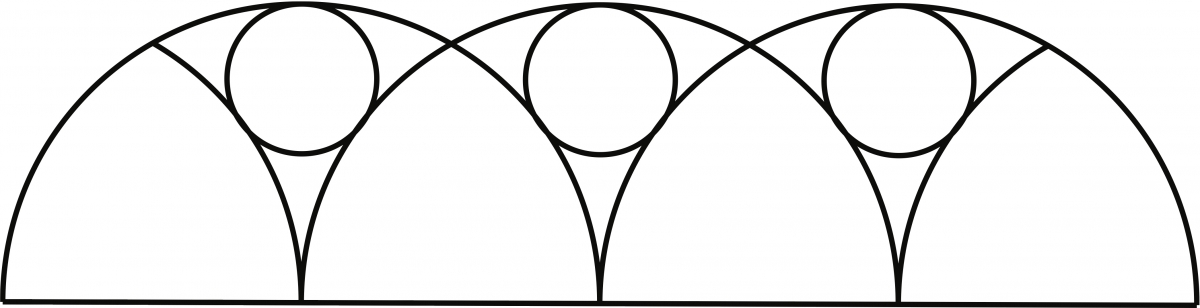
For our final example, we highlight one of the many beautiful illustrations of Gothic tracery. This design, shown in Figure 14, is found on page 269 in the subsection Forms containing tangent circles: algebraic analysis. Here, we start with a semicircle. Sykes described the construction as follows: “\(AB\) is the diameter of the semicircle \(ACB\). \(A\) and \(B\) are the centers and \(\frac{1}{2} AB\) the radius for the arcs \(DE\) and \(DF\). Circle \(O\) is tangent to the arcs as shown.” By tangent, Sykes meant that the circle with center \(O\) touches both the arcs \(DE\) and \(DF\), as well as the semicircle \(ACB\). For this design, as the title of the subsection suggests, we will need algebra in addition to geometry in order to construct the necessary tangent circle described above.
Figure 14: From Great Waltham Church, Essex, England.
At first the reader may be unsure how to proceed when constructing the tangent circle, but Sykes provided the key to solving this problem in the following exercise with added suggestion: “If \(AB = s\), find the radius of circle \(O\). Suggestion: Let the radius of circle \(O\) be \(r\). \(\triangle ODB\) gives the equation, \[\left(\frac{s}{2}\right)^2+\left(\frac{s}{2}-r\right)^2=\left(\frac{s}{2}+r\right)^2."\] Solving for \(r\) in terms of \(s\) gives us \(r = s/8\). Sykes’ follow-up question asked the reader to “show how to construct the entire figure.”
An example of a wood carving with this semicircular design, as shown in Figure 15, can be found in St. Andrew’s Church in Folkingham, England.
Figure 15: Decorated blind tracery (c.1330) in a lower panel of the rood screen, the Church of St Andrew, Folkingham, Lincolnshire. (Photograph by Spencer Means, August 17, 2014, www.flickr.com/photos/hunky_punk/15885732179, licensed under the Creative Commons Attribution-Share Alike 2.0 Generic license.)
It is easy to see how to extend the designs given in our first four examples since each is based on a square. With a semicircle, while at first glance it may appear difficult to extend a single copy of the design, it is still possible as demonstrated by the three overlapping design copies shown in Figure 16.
Figure 16: Gothic Tracery: Forms containing tangent circles.
With over 450 drawings and illustrations and over 1800 exercises, we have barely scratched the surface of the breadth of available problems and historical references. We have included some of her other designs in our own geometry book [4], and we encourage the reader to seek out Sykes’ work [40] as it provides beautiful examples of how geometry is used in architecture and industrial design.
Maureen T. Carroll (University of Scranton) and Elyn Rykken (Muhlenberg College), "Mabel Sykes: A Life Untold and an Architectural Geometry Book Rediscovered – The Source Book," Convergence (February 2020)