- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematical Treasure: William Oughtred’s The Key of the Mathematicks
Brief Biography
William Oughtred (1574-1660) was born at Eton and educated at King’s College, Cambridge University, where he became a fellow and where his father, Benjamin Oughtred (d. 1618), was a writing-master and registrar. He earned his BA in 1596 and MA in 1600, during a period in which he began to study mathematics intensively. In 1603, he left Cambridge to live in Shalford, where he married Christsgift Caryll. In 1610 he became rector of Albury, where he remained the rest of his life.
Oughtred corresponded with Henry Briggs, of common logarithm fame, and Edmund Gunter, who invented Gunter’s chain, quadrant, and scale. Around 1628 he was appointed by the Earl of Arundel to teach his son mathematics. At about this time he was inspired to write Clavis Mathematicae (The Key to Mathematics), published in 1631. Oughtred offered free mathematical tutoring to pupils and maintained mathematical correspondence with colleagues, positively affecting a new generation of mathematicians that included Seth Ward, John Wallis, and Christopher Wren.
His invention of the slide rule involved Oughtred in a priority dispute over his claim that he was the first to invent a slide rule based on logarithms. Historical perspective validates that it was Oughtred who in 1622 first used two logarithmic scales sliding against one another to perform multiplication and division; the idea for the slide rule might have been inspired by reading Napier’s works and from corresponding with Henry Briggs. Oughtred also introduced the "X" for multiplication, the abbreviations "sin" and "cos" for the trigonometric functions sine and cosine, and "::" as the symbol for proportion. Pedagogically, he argued that in mathematics teaching, theory should precede practice, and that algebra needed to become more symbolic in its notation. Besides mathematics, he had a lifetime interest in alchemy and astrology, which were both common areas of interest for Renaissance and early modern natural philosophers.
William Oughtred remained a rector until his death in 1660 at Albury, a month after the restoration of Charles II. Oughtred's name is remembered in the Oughtred Society, a group formed in the United States in 1991 for slide rule collectors; this author is a long time member of that society, which produces an interesting biannual journal mainly devoted to analogue computing devices and holds meetings and slide rule auctions.

Cover page of Journal of the Oughtred Society, Spring 2016. Personal photo.
The Key of the Mathematicks, 1647


Title page and fold-out frontispiece portrait. From the collection of Dr. Sid Kolpas.
This is the first English edition of Oughtred’s Clavis (Key), translated by Robert Wood of Lincoln College, Oxford. It is a complete translation of Oughtred’s 1631 original Clavis Mathematicae, augmented with a work on creating sundials by using geometrical construction without having to use trigonometry, by the help of a volvelle. Oughtred wrote this work, Easy Way of Delineating Sun-Dials by Geometry, when he was between twenty-two and twenty-three, but it did not appear in print until this 1647 edition. Sundials were a topic of great interest since there were neither watches nor pendulum clocks in Oughtred’s time. It is interesting to note that there are still sundials at the Cambridge campus. The added work was repeated in subsequent Latin editions of Clavis but was not included in the 1694 English translation by Edmund Halley. While the original Latin edition made Oughtred well known among mathematicians, the 1647 English version brought him celebrity with mathematical practitioners and craftsmen since it was written in English and was thus able to be read by more people. The 1647 edition makes use of Oughtred’s vertical stroke as the decimal separator. This concise work also contained algebra through the use of symbols, some of which, like "X" for multiplication and "::" for proportion, were invented by Oughtred.

1647 printing of Most easie way for the delineation of Plaine Sun-dials.
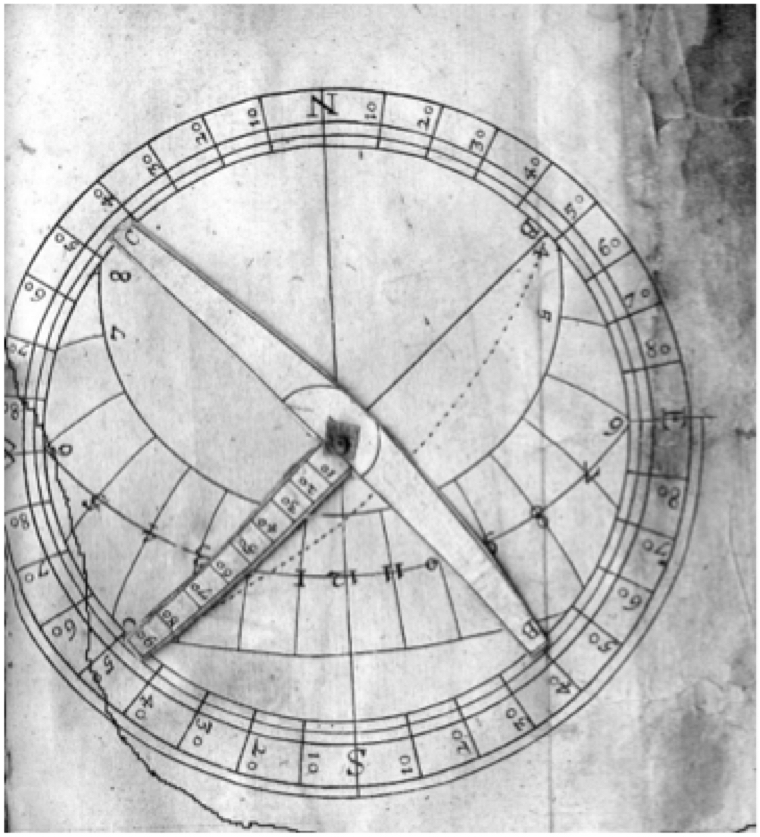
Volvelle from The Key of the Mathematicks, used for plane sundials.
A volvelle is a type of slide chart made of paper and constructed with rotating parts. Volvelles are considered early examples of analog computers.
Some Examples

Oughtred introduced the multiplication sign (X) and a vertical line (|) to separate whole numbers from decimals.

A table of powers: q means squared, c means cubed, and qqc represents the 7th power. Later in the seventeenth century, Descartes popularized the use of superscript whole number exponents in his Geometry.

Raising (A + E) to consecutive powers. Note that the coefficients form Pascal’s Triangle. Also note that for (A + E)4 Oughtred missed the coefficient 4 for AcE (A3E).

(A+E)(A-E)=A2-E2
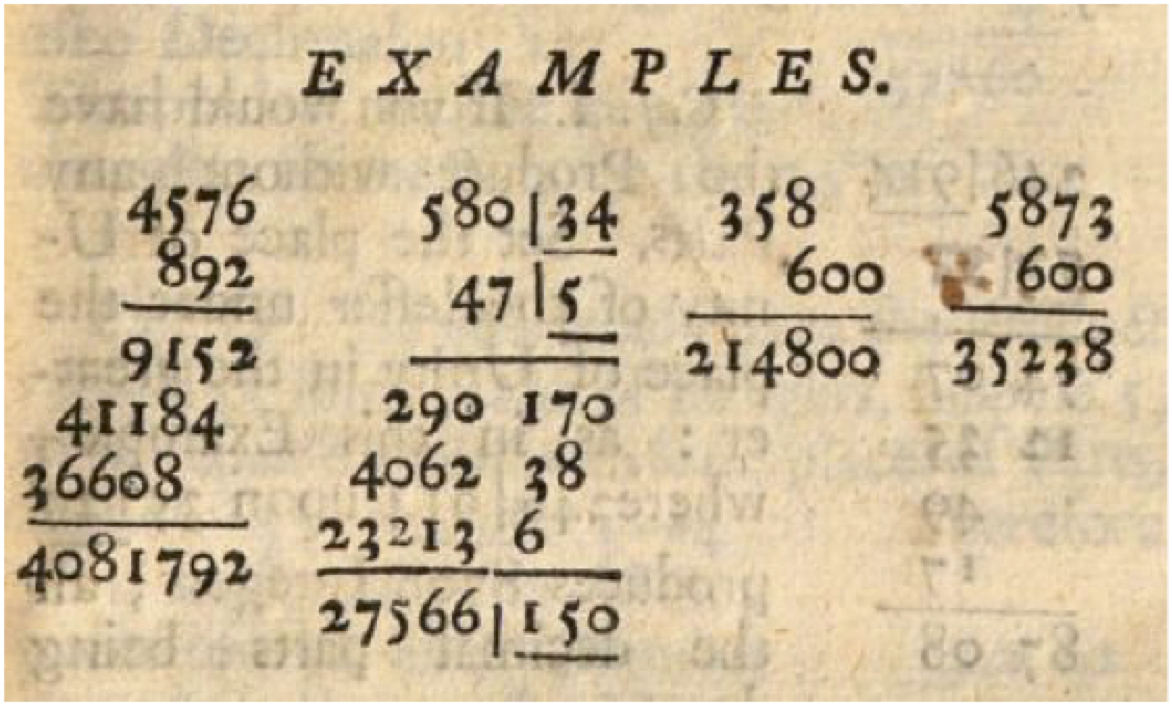
Multiplication examples. Note the vertical line to separate decimals.

7/9 is in the same proportion as 28/Q. Therefore 9 X 28/7 = Q.
Use in the classroom
Instructors can use images from this work to provide examples of the historical development of algebra, or use examples from this work in the algebra classroom for enrichment. If one’s institution has an account with Proquest (http://www.proquest.com/libraries/academic/databases/), a digital copy is available.
References
Cajori, Florian. William Oughtred, a great seventeenth-century teacher of Mathematics. Chicago and London: Open Court, 1916.
Oughtred Society. http://www.oughtred.org/.
Oughtred, William. The Key of the Mathematicks. London: Thomas Harper, 1647.
Tomash, Erwin. The Erwin Tomash Library Catalogue. http://www.cbi.umn.edu/hostedpublications/Tomash/.
Sidney J. Kolpas (Delaware County Community College), "Mathematical Treasure: William Oughtred’s The Key of the Mathematicks," Convergence (March 2017)




