- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
More Classroom Activities Based on Ancient Indian Rope Geometry - Transforming a square into a rectangle of equal area
The applet directly below demonstrates the method found in Section 2.4 of the Śulba-sūtra of Baudhāyana (BSS 2.4) for transforming a square into a rectangle of equal area. Click “Go” to advance to the next step and “Reset” when the construction is completed. The dimensions of the given square can be adjusted by sliding points \(A\) and \(D.\) The longer side of the desired rectangle can be adjusted by sliding point \(E.\) Slide point \(P\) to \(E\) to make the area of rectangle \(DFHI\) equal to that of \(ABDC.\)
The problem of transforming a square into a rectangle of equal area was considered by Baudhāyana in Sections 2.3-2.4 of BSS [Sen and Bag, p. 79].
2.3 – A square intended to be transformed into a rectangle is cut off by its diagonal. One portion is divided into two (equal) parts which are placed on the two sides (of the other portion) so as to fit (them exactly).
2.4 – Or else, if a square is to be transformed (into a rectangle), (a segment) of it is to be cut off by the side (of the rectangle); what is left out (of the square) is added to the other side…
It is clear that the intention of BSS 2.3 is to produce a rectangle of equal area, with one side of the rectangle having length equal to the diagonal of the square. The figures below demonstrate this. Say we wish to construct a rectangle with area equal to that of square \(ABDC\) and with one side length equal to the length of the square’s diagonal. The construction is rather simple: just divide the square in two pieces along the diagonal. Mark \(M,\) the midpoint of the diagonal, further dividing triangle \(ABC\) into two congruent triangles \(ABM\) and \(ACM,\) the areas of which are of course one fourth of the area of the square. Then construct congruent triangles \(ABF\) and \(ACE\) (say by reflecting \(ABM\) and \(ACM,\) respectively). The area of rectangle \(BCEF\) evidently equals that of \(ABDC,\) as it is just 4 times the area of \(ABM.\)
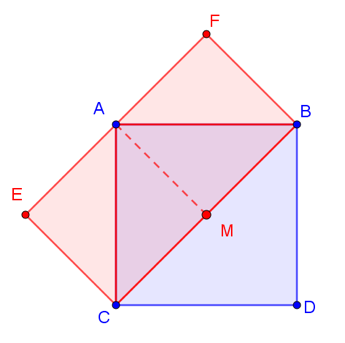
Figure 2. Construction of rectangle \(BCEF\) with area equal to that of square \(ABDC\) and one side being the diagonal of the square.
There are challenges in interpreting exactly what Baudhāyana intended in BSS 2.4. The same rule is given in 3.1 of the Śulba-sūtra of Āpastamba, and also with no clear interpretation and missing details (see, for example, the discussion on p. 159 of [Sen and Bag]). The method presented here for transforming a square into a rectangle of any side lengths is due to Datta, and captures the spirit of Baudhāyana’s method [Datta]. This is a more general approach than that found in 2.3 because we have the freedom to choose one of the side lengths of the rectangle.
To begin the construction, start with a square \(ABDC.\) Now there are an infinite number of non-square rectangles with area equal to that of the square, but once we have fixed one of the side lengths, say \(L_1,\) the other side length is of course determined: \[L_2=\frac{{\rm{Area}}(ABDC)}{L_1}.\] Evidently, one side length will be less than the square side length, and one will be greater. Without loss of generality, suppose \(L_1\) is the greater one. Datta’s method allows us to choose the greater side length. First, we extend segment \(AC\) to \(CE,\) so the length of \(CE\) is \(L_1.\) Similarly, extend \(BD\) to \(DF\) so that \(DF\) has length \(L_1.\) We have constructed a rectangle \(CEFD\) which has one side length equal to that of the given square, and one side length equal to the desired side length \(L_1.\) Let \(P\) be a point on side \(EF.\) Extend a rope from point \(P\) to \(D.\) The rope will intersect side \(AB\) at a point, say \(G.\) Now the length of segment \(BG\) is taken to be the second side length of the desired rectangle.
Now consider the red rectangle \(DIHF.\) In the applet, one may slide point \(P\) along segment \(EF\) to see how the area of \(DIHF\) (and position of \(G\)) changes. When point \(P\) meets point \(E,\) we see that \(DIHF\) is the desired rectangle. To prove this, first slide point \(P\) to point \(D,\) and note the area of \(CEFD\) is split into two by segment \(DP:\)
\[\frac{1}{2}{\rm{Area}}(CEFD)= {\rm{Area(Triangle}}(GHP))+{\rm{Area(Rect}}(BGHF))+{\rm{Area(Triangle}}(BDG)).\]
\[\frac{1}{2}{\rm{Area}}(CEFD)= {\rm{Area(Triangle}}(AGP))+{\rm{Area(Rect}}(AGIC))+{\rm{Area(Triangle}}(DIG)).\]
By symmetry,
\[{\rm{Area(Triangle}}(GHP))={\rm{Area(Triangle}}(AGP))\]
and
\[{\rm{Area(Triangle}}(BDG))={\rm{Area(Triangle}}(DIG)).\]
Therefore, combining the above equations allows us to infer
\[{\rm{Area(Rect}}(BGHF))={\rm{Area(Rect}}(AGIC)).\]
Thus \[{\rm{Area}}(DIHF)={\rm{Area}}(BGHF)+{\rm{Area}}(BDIG)={\rm{Area}}(AGIC)+{\rm{Area}}(BDIG)={\rm{Area}}(ABDC),\] as required.
Cynthia J. Huffman and Scott V. Thuong (Pittsburg State University), "More Classroom Activities Based on Ancient Indian Rope Geometry - Transforming a square into a rectangle of equal area," Convergence (May 2018)




